线性回归demo数据-参数配置

# 先传入数据，可以是手动定义，也可以导入，这边就直接拿一条直线y=2x+1，来进行模拟了。
# 构造x和y(x的值为0-10)(y的值为2x+1)
x_value = [i for i in range(11)]
y_value = [2*i+1 for i in x_value]
# 由于都是列表(数组)，也就是需要转化为torch可以接受的模式
# np.array是将一个数组转化为张量.
# reshape即将张量的格式进行修改
x_train = np.array(x_value,dtype=np.float32)
y_train = np.array(y_value,dtype=np.float32)
x_train = x_train.reshape(-1,1)
y_train = y_train.reshape(-1,1)
# 导入包
import torch
import torch.nn as nn
# 线性回归模型
class LinearRegressionModel(nn.Module) :
    def __init__(self,input_dim,out_dim):
        super(LinearRegressionModel,self).__init__()
        # 这里是构造一个全连接层
        self.linear = nn.Linear(input_dim,out_dim)
    # 创建x与y的构建，即此处判定了输出入x即得到y的一条线性链
    def forward(self,x):
        y = self.linear(x)
        return y

input_dim = 1
out_dim = 1
model = LinearRegressionModel(input_dim,out_dim)
# 指定好参数以及损失函数
# epochs训练次数 learning_rate学习率
# SGD是一个优化器，前一个参数代表着需要优化的参数，后一个是学习率，具体一点他是一个随机梯度优化器
# MSELoss是一个损失函数，目的是用来计算出L的
epochs = 1000
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)
criterion = nn.MSELoss()

关于linear的理解：链接
关于SGD的理解：链接
关于MSELoss损失函数的理解：链接

线性回归demo数据-训练回归模型

# 指定好参数以及损失函数
# epochs训练次数 learning_rate学习率
# SGD是一个优化器，前一个参数代表着需要优化的参数，后一个是学习率，具体一点他是一个随机梯度优化器
# MSELoss是一个损失函数，目的是用来计算出L的
epochs = 1000
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)
criterion = nn.MSELoss()
# 训练回归模型
for epho in range(epochs):
    epho+=1
    # 转化为tensor
    inputs = torch.from_numpy(x_train)
    labels = torch.from_numpy(y_train)
    # 梯度每一步都需要清零
    optimizer.zero_grad()
    # 前向传播
    outputs = model.forward(inputs)
    # 计算损失值
    loss = criterion(outputs,labels)
    # 反向传播
    loss.backward()
    # 更新权重参数
    optimizer.step()

测试数据：

# 测试模型预测的结果
predicted = model(torch.from_numpy(x_train).requires_grad_()).data.numpy()
print(predicted)

输出结果：

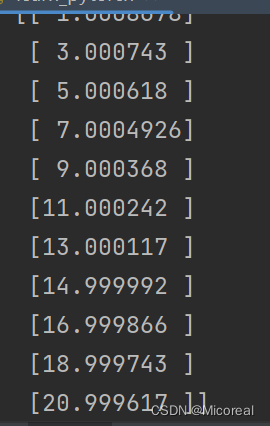
# 模型的保存以及提取
torch.save(model.state_dict(),'model.pkl')
model.load_state_dict(torch.load('model.pkl'))

总结以及关于GPU的训练：(仅有两处不同)

# 线性回归
# 先传入数据，可以是手动定义，也可以导入，这边就直接拿一条直线y=2x+1，来进行模拟了。
# 构造x和y(x的值为0-10)(y的值为2x+1)
x_value = [i for i in range(11)]
y_value = [2*i+1 for i in x_value]
# 由于都是列表(数组)，也就是需要转化为torch可以接受的模式
# np.array是将一个数组转化为张量.
# reshape即将张量的格式进行修改
x_train = np.array(x_value,dtype=np.float32)
y_train = np.array(y_value,dtype=np.float32)
x_train = x_train.reshape(-1,1)
y_train = y_train.reshape(-1,1)
# 导入包
import torch
import torch.nn as nn
# 线性回归模型
class LinearRegressionModel(nn.Module) :
    def __init__(self,input_dim,out_dim):
        super(LinearRegressionModel,self).__init__()
        # 这里是构造一个全连接层
        self.linear = nn.Linear(input_dim,out_dim)
    # 创建x与y的构建，即此处判定了输出入x即得到y的一条线性链
    def forward(self,x):
        y = self.linear(x)
        return y

input_dim = 1
out_dim = 1
model = LinearRegressionModel(input_dim,out_dim)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~不同处1~~~~~~~~~~~~~~~~~~~~~~~~~~~
device = torch.device("cuda:0"if torch.cuda.is_available() else "cpu")
model.to(device)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

# 指定好参数以及损失函数
# epochs训练次数 learning_rate学习率
# SGD是一个优化器，前一个参数代表着需要优化的参数，后一个是学习率，具体一点他是一个随机梯度优化器
# MSELoss是一个损失函数，目的是用来计算出L的
epochs = 1000
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)
criterion = nn.MSELoss()
# 训练回归模型
for epho in range(epochs):
    epho+=1
    
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~不同点2~~~~~~~~~~~~~~~~~~~
    # 转化为tensor
    inputs = torch.from_numpy(x_train).to(device)
    labels = torch.from_numpy(y_train).to(device)
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
    # 梯度每一步都需要清零
    optimizer.zero_grad()
    # 前向传播
    outputs = model.forward(inputs)
    # 计算损失值
    loss = criterion(outputs,labels)
    # 反向传播
    loss.backward()
    # 更新权重参数
    optimizer.step()
    # if epho%100==0 :
    #     print(loss.item())
# 测试模型预测的结果
predicted = model(torch.from_numpy(x_train).requires_grad_()).data.numpy()
print(predicted)
# 模型的保存以及提取
torch.save(model.state_dict(),'model.pkl')
model.load_state_dict(torch.load('model.pkl'))

常见的tensor格式

常见的tensor格式主要有下面四种：

1. scalar
2. vector
3. matrix
4. n-dimensional tensor

scalar

代表着一个值：

x = tensor(42)
print(x)
print(x.dim())# 维度
print(x.item())

输出结果：

vector

x = tensor([1,2,3])
print(x)
print(x.dim())
print(x.size())

输出结果：

matrix

基本上也是一致的，只是维度扩展了。