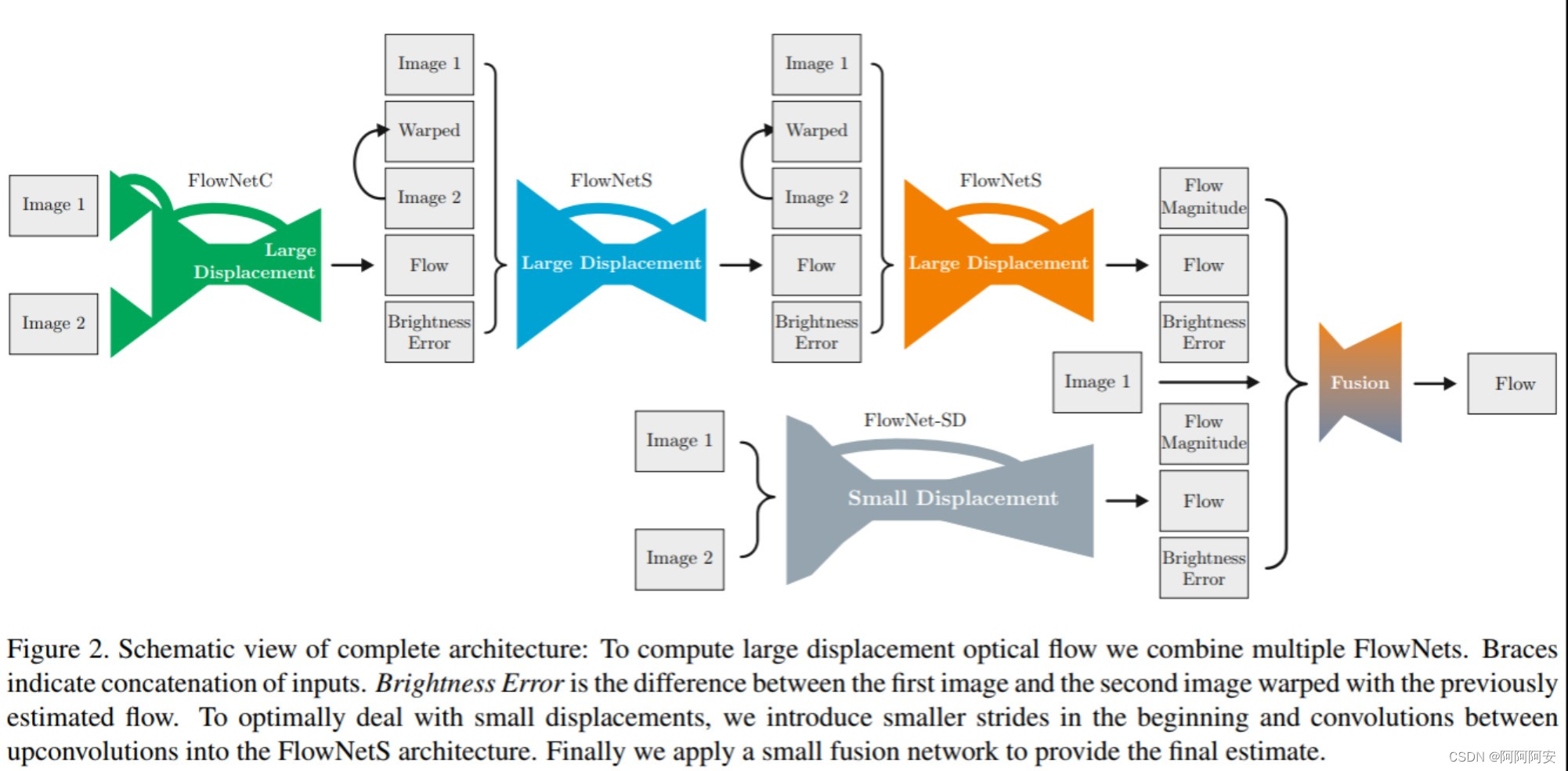
1 介绍

1. 有监督的降维

2. 投影后类内方差最小，类间方差最大

2 推导

我们记最佳的投影向量为w，那么一个样例x到方向向量w上的投影可以表示为：
- $y=w^Tx$
给定数据集
- 令 $N_i,X_i,\mu_i,\Sigma_i$ 分别表示第i类的样本个数、样本集合、均值向量和协方差矩阵
- - ——>在投影上的均值是 $w^\top \mu_i$
- '
  - ——>在投影上的协方差是 $\tilde S_i^2=\sum_{x \in X_i} (w^\top x-w^\top \mu_i)(w^\top x-w^\top \mu_i)^\top=\sum_{x \in X_i} w^\top(x-\mu_i)(x- \mu_i)^\top w$
我们希望两个类尽可能地远，类内部尽可能地近
- ——>在投影上两个类的均值差距越大越好
  - $J_1(w)=||w^\top \mu_0 -w^\top \mu_1||_2^2=w^\top(\mu_0-\mu_1)(\mu_0-\mu_1)^\top w$ 越大越好
  - 记类间散度矩阵 $S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^\top$ （between）
  - 则 $J_1(w)=w^TS_bw$
- ——>在投影上同一类的均值接近
  - $J_2(w)=S_1^2+S_2^2 =\sum_{x \in X_1} w^\top(x-\mu_1)(x- \mu_1)^\top w+\sum_{x \in X_2} w^\top(x-\mu_2)(x- \mu_2)^\top w$ $= w^\top[\sum_{x \in X_1}(x-\mu_1)(x- \mu_1)^\top +\sum_{x \in X_2} (x-\mu_2)(x- \mu_2)^\top] w$ 越小越好
  - 记类内散度矩阵 $S_w=\sum_{x \in X_1}(x-\mu_1)(x- \mu_1)^\top +\sum_{x \in X_2} (x-\mu_2)(x- \mu_2)^\top$ (within)
  - $J_2(w)=w^TS_ww$
- 将J1(w)和J2(w)的要求合并在一块，有：越大越好
  - $J(w)=\frac{w^\top S_b w}{w^\top S_w w}$
  - 上式又称为Sb和Sw的广义瑞利商

3 确定w

w是一个向量，我们只需要知道它的方向即可。向量的模任何大小是都可以的【(a,b)和(ka,kb)都是合理的向量】
所以我们一定可以找到一个w，使得 $w^\top S_w w=1$
于是我们的目标函数变成
- 使用拉格朗日乘子法，有：
- - $(\mu_0-\mu_1)^\top w$ 是一个标量，所以 $S_b w$ 的方向和 $\mu_0-\mu_1$ 的方向相同/相反
  - 我们记 $S_b w= \lambda_1 (\mu_0-\mu_1)$
  - 于是 $\lambda_1 (\mu_0-\mu_1)=\lambda S_w w$
  - 所以 $w=\frac{\lambda_1}{\lambda} S_w^{-1}(\mu_0-\mu_1)$
  - 对于w，其向量长度可以任意，只要知道他的方向即可，所以我们把前面的λ1/λ去掉，于是有：
- $w=S_w^{-1}(\mu_0-\mu_1)$
- 也就是说，通过原始样本两个类的均值和方差，就可以确定最佳的投影方位

4 sklearn

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])

clf = LinearDiscriminantAnalysis()
#n_components是一个参数，设置降维至多少
#如果这个参数没有设置，那么就默认是min(n_classes-1,n_features)

clf.fit(X, y)

参考内容：LDA线性判别分析 - 知乎 (zhihu.com)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/179953.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！