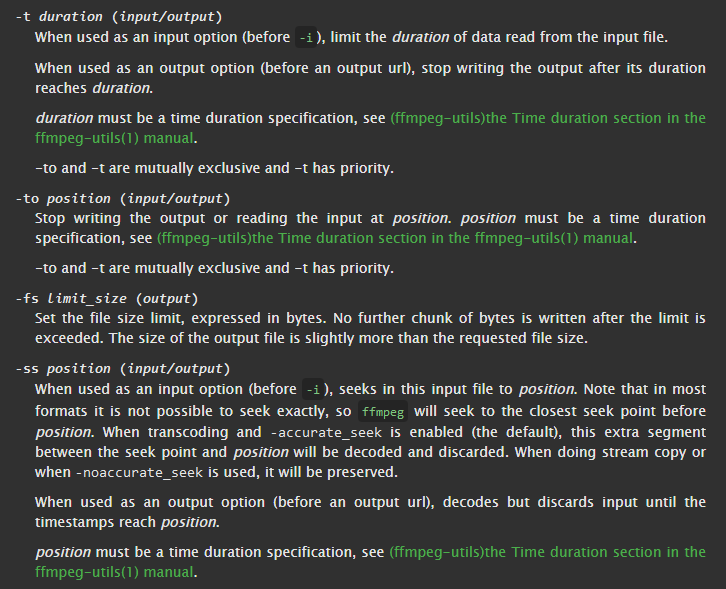
函数介绍

使用fmincon函数来进行求解，格式为

[x,y] = fmincon(f,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

其中，f表示所求的目标函数，x0表示初始值，A,b,Aeq,beq表示线性的约束，lb,ub表示上界和下届，nonlcon表示非线性的约束，x表示取得最小值时的值，y表示取得的最小值。

当参数某一项为空，可以设置成[]，例如约束$x>1$可以设置成lb=1，ub=[]。

设置函数参数

$$minf(x)=x_1^2+x_2^2$$
$$s.t.x_1^2>1;x_2^2>5$$
将目标函数调整成标准的形式
$x_1^2-1>0,x_2^2-5>0$

针对此优化问题，约束条件里没有线性的约束，则A,b,Aeq,beq设置成[]，然后只需建立非线性约束的函数即可。

步骤

首先建立目标函数的m文件

function f = fun1(x)
        f = x(1)^2 + x(2)^2;
end

然后建立约束的m文件

function [g,h] = fun2(x)
        g=[x(1)^2-1 
            x(2)^2-5];
        h=[];
end

其中，g表示不等约束，h表示等式约束
最后建立主函数

clc;clear;close all 
[x,y] = fmincon('fun1',[1;1],[],[],[],[],[],[],'fun2')

这里设置的初始值为[1;1]

结果分析

经过运算得到

然后对所得到的结果进行验证
通过穷举方法进行画图

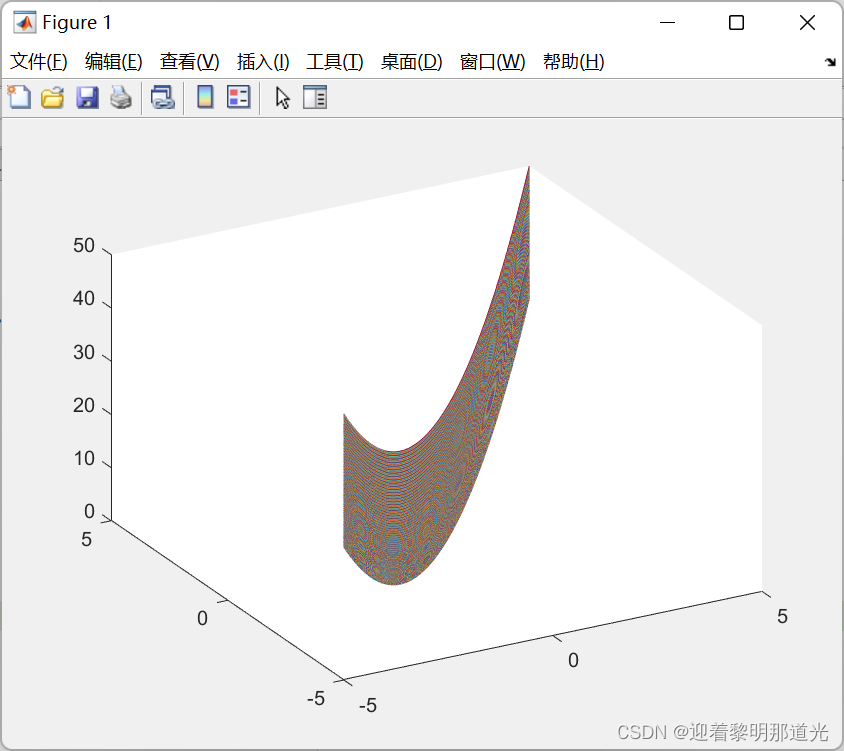
从图中可以得到当最优点趋近（0，0）时候，目标函数的值更小，而上面计算出来的结果非常接近，因此得到的结果正确。