一、栈在括号匹配中的应用

数据结构之栈_迷茫中的小伙的博客-CSDN博客_数据结构之栈栈括号和队列的应用

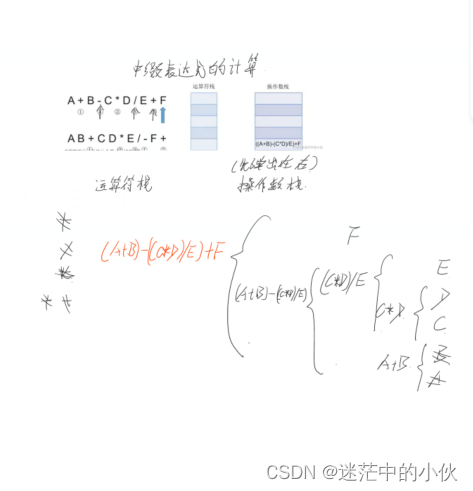
二、栈在表达式求值中的应用

中缀转 ->后缀  ： 左右先 (左边能先算,先算左边,因为这样可以保证确定性,即计算机运算的方式)

后缀转->中缀  ：从前往后扫描(因为符号是放在后面的,只有找到数字才能进行匹配,所以从前往后扫描)

总结:  上面是中缀和后缀,差个前 ,所以都是从前开始,或者从左开始(左 = 前)

           后缀->中缀在栈中的运算,先弹出的是右操作数 (右 = 后)

-------------------------------------------------------------------------------------------------------------------------------

中缀->前缀  : 右优先
前缀->中缀  : 从后往前

总结: 上面只有中缀和前缀,所以差个后缀,所以从后往前或者从右开始( 右 = 后)
          前缀->中缀在栈中的运算,先弹出的是左操作数(前 = 左)

三、机算