主要只搞了一个这道题，有点摸鱼了今天晚上，也是来小看一下这道题吧
01背包+完全背包

P1941 [NOIP2014 提高组] 飞扬的小鸟

 

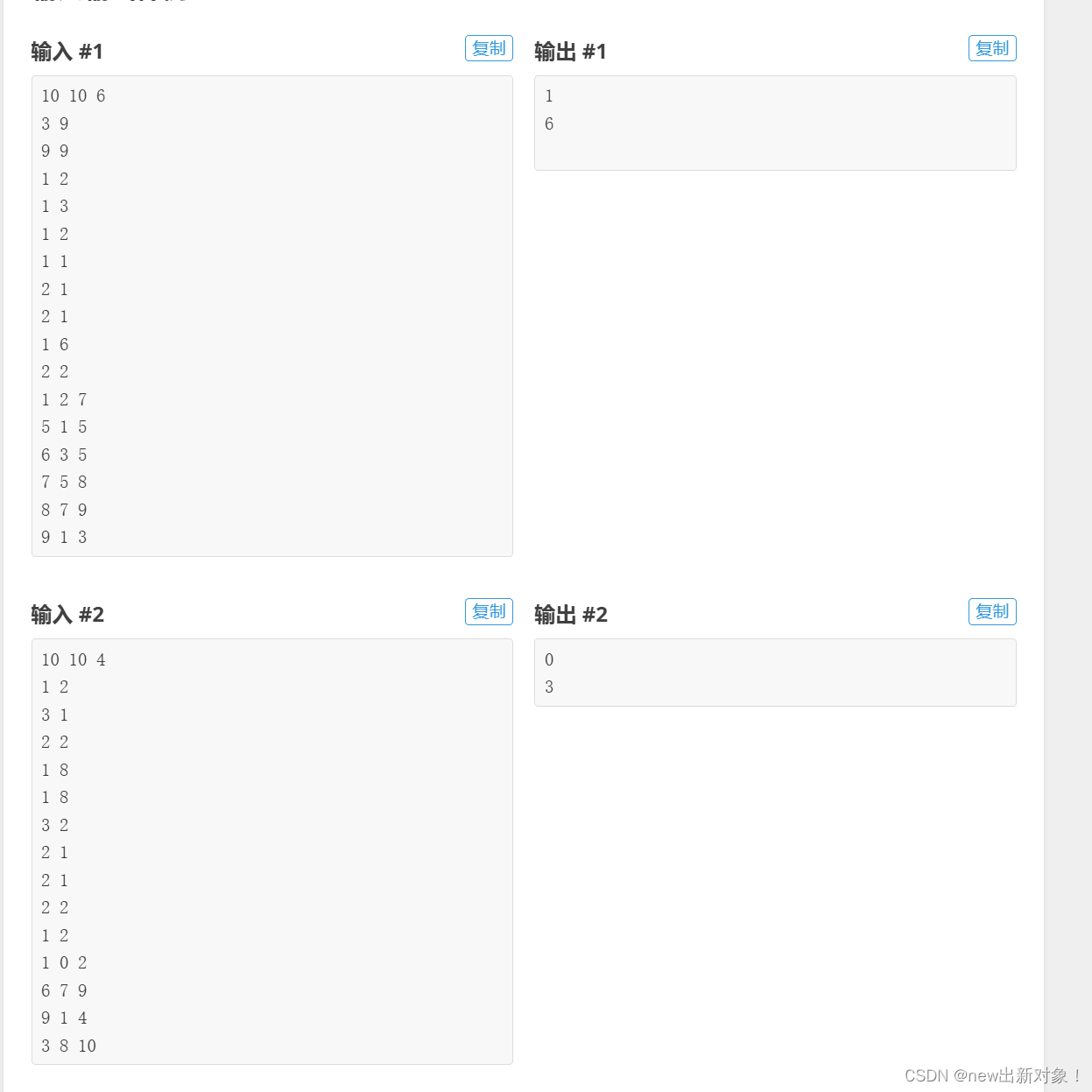
题意： 

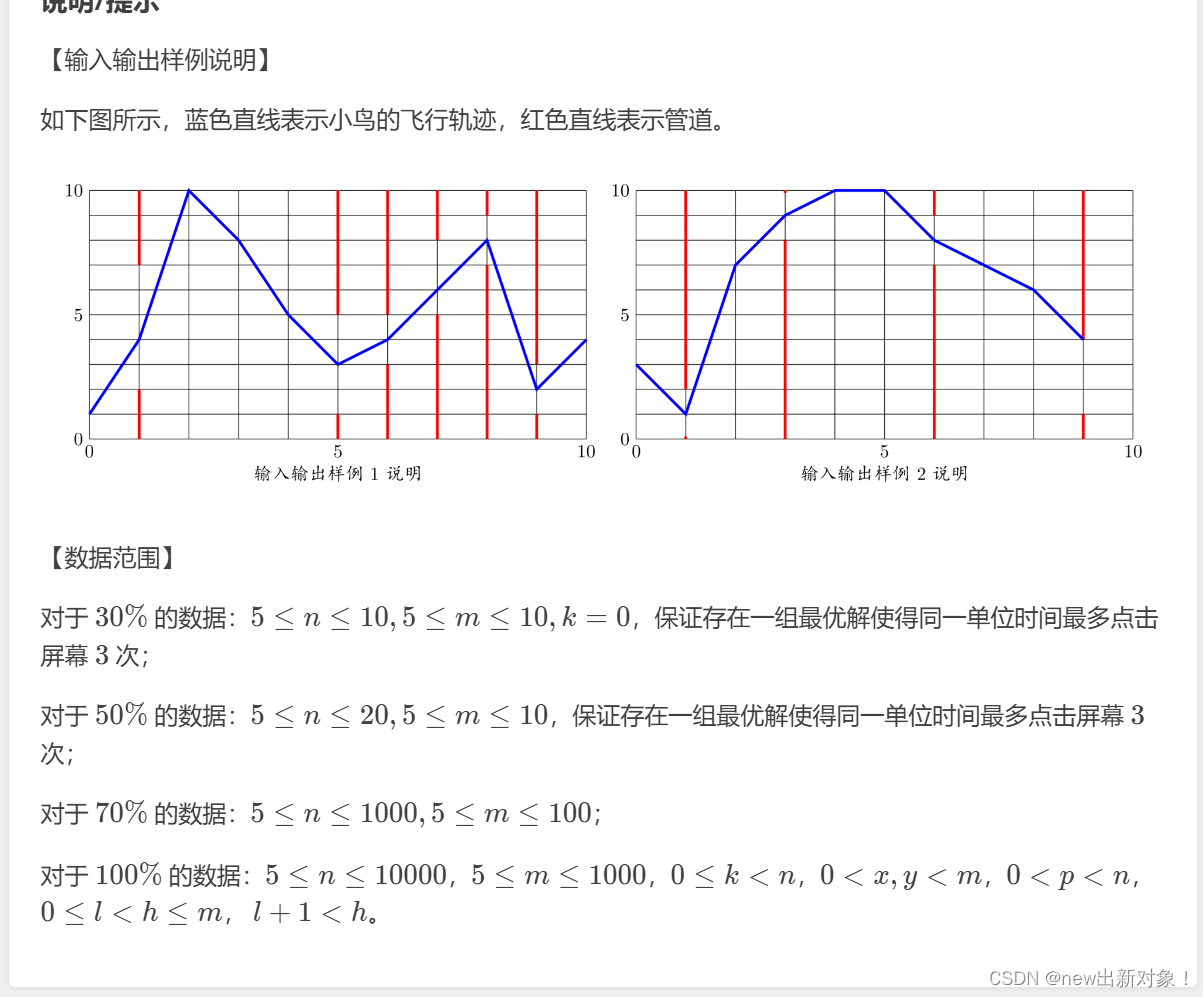
这题是说，给我们一个游戏界面，界面的长度为n（水平距离），高度为m（竖直距离），然后有k个管子，告诉你他下沿部分长度和下沿部分长度，然后对于每单位的水平距离，都有相应的x[i]上升距离和y[i]下降距离，然后问你达到游戏地图的最右端的最小步数是多少，要是无法达到最右端，问你最多能通过几个管子

思路：

对于这题很明显是背包类问题，然后就是01背包+完全背包

首先，我们对于每单位位置都有两种操作，可以选择点击屏幕上升，也可以选择不点下降（两种状态，01背包）

我们对于每个位置的点也分为两种情况，可以选择只点一次，也可以选择，点击多次（完全背包）

那么我们就可以定义dp数组，dp[ i ] [ j ],表示到达位置i,j的最小步数为dp[ i ] [ j ]

然后我们的状态转移方程需要判断四种情况

（1）上升:dp[i][j]=min(dp[i-1][j-x[i]]+1,dp[i][j-x[i]]+1);

（2）上升到天花板:dp[i][m]=min(dp[i][m],dp[i][j]);

（3）下降:dp[i][j]=min(dp[i-1][j+y[i]],dp[i][j]);

（4）不合法的位置，一定会被拦截:dp[i][j]=dp[0][0];  

然后我们去判断最右端位置是否存在合法数值即可，如果存在则证明可以达到最右端，反之则不行，需要求出过几个管道,求管道的时候要逆序去找，先找哪一列存在合法数据，然后定位这个长度，去看这个长度里面有几个管子

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
int x[10005];
int y[10005];
int low[10005];
int high[10005];
int dp[10005][2005];
int vis[10005];

int main()
{
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
	cin>>x[i]>>y[i];
	for(int i=1;i<=n;i++)
	{
		low[i]=1;
		high[i]=m;
	}
	int a,b,c;
	for(int i=1;i<=k;i++)
	{
		cin>>a>>b>>c;
		vis[a]=1;
		low[a]=b+1;
		high[a]=c-1;
	}
	memset(dp,0x3f3f3f3f,sizeof(dp));
	for(int j=1;j<=m;j++)
	dp[0][j]=0;
	
	for(int i=1;i<=n;i++)
	{
		for(int j=x[i]+1;j<=m+x[i];j++)
		{
			dp[i][j]=min(dp[i-1][j-x[i]]+1,dp[i][j-x[i]]+1);
		}
		
		for(int j=m+1;j<=m+x[i];j++)
		{
			dp[i][m]=min(dp[i][m],dp[i][j]);
		}
		
		for(int j=1;j<=m-y[i];j++)
		{
			dp[i][j]=min(dp[i-1][j+y[i]],dp[i][j]);
		}
		
		for(int j=1;j<low[i];j++)
		{
			dp[i][j]=dp[0][0];
		}
		for(int j=high[i]+1;j<=m;j++)
        {
        	dp[i][j]=dp[0][0];  
		}
	}
	int ans=0x3f3f3f3f;
	for(int j=1;j<=m;j++)
	{
		ans=min(dp[n][j],ans);
	}
	if(ans<0x3f3f3f3f)
	{
		cout<<1<<"\n";
		cout<<ans<<"\n";
	}
	else
	{
		int i,j;
		for(i=n;i>=1;i--)
		{
			for(j=1;j<=m;j++)
			{
				if(dp[i][j]<0x3f3f3f3f)
				break;
			}
			if(j<=m)
			break;
		}
		int sum=0;
		for(int j=1;j<=i;j++)
		{
			if(vis[j]==1)
			sum++;
		}
		cout<<0<<"\n";
		cout<<sum<<"\n";
	}
	return 0;
}