一、简介

在本次研究中，我们对2018年硕士生考试成绩数据进行了深入的统计分析。这项分析旨在探索不同因素如性别、生源背景、基因型以及出生月份等对学生成绩的潜在影响。我们使用了一系列的统计方法，包括描述性统计分析、相关性分析、分组分析以及方差分析（ANOVA），以获得对这些数据的全面理解。这些方法不仅帮助我们洞察数据的基本特性，还揭示了不同变量之间的相互关系。

二、主要过程

首先进行问题分析：

描述性统计分析：计算平均分、中位数、标准差等，以了解成绩的总体分布情况。

性别差异分析：比较男女学生在各科目及总分上的表现差异。

生源背景分析：探究学生的生源背景（城镇或农村）对成绩的可能影响。

基因型分析：检查不同基因型（gene1和gene2）与成绩之间的关系。

生日与成绩的关系：分析学生的出生日期是否与成绩表现有关联。

首先读取数据：

完整代码和数据

import pandas as pd
from io import StringIO
import numpy as np

data_df = pd.read_csv("C:/Users/Administrator/Desktop/data3.csv", encoding='gbk')
data_df 

进行描述性统计分析

	名词	填空	简答	计算	综合	生日
mean	23.57	16.202	14.340	16.945	71.208	1989-07-08 04:45:19
min	10	3	6	4	48.5	1986-01-05 00:00:00
25%	19	15	11	13	62.75	1988-11-12 12:00:00
50%	26	16	15	16	72	1989-08-23 00:00:00
75%	27	18	17	20	79.5	1990-03-17 00:00:00
max	30	20.5	20	29	94.5	1998-11-15 00:00:00
std	4.589309	2.280534	3.597774	5.052427	10.97635	1989-07-08 04:45:19

平均分（总分）：71.21分

最高分（总分）：94.5分

最低分（总分）：48.5分

总体上，学生的成绩分布在48.5分到94.5分之间，平均成绩为71.21分。

# 性别差异分析
gender_diff = data_df.groupby('性别').mean()
gender_diff

性别差异分析

	名词	填空	简答	计算	综合
性别
F	24.184739	16.329317	14.433735	17.112450	72.222892
M	23.038462	16.092657	14.258741	16.800699	70.325175

接下来可视化一下：

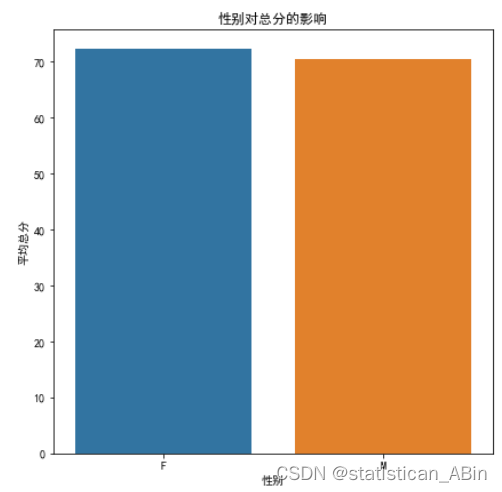
# 男生平均总分：70.63分
# 女生平均总分：72.22分
# 女生在平均总分上略高于男生。

# 生源背景分析
origin_diff = data_df.groupby('生源').mean()
origin_diff

接下来可视化一下：

# 创建一个画布和子图
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
import seaborn as sns
fig, axes = plt.subplots(2, 3, figsize=(18, 12))

# 性别差异分析可视化
sns.barplot(x=gender_diff.index, y="综合", data=gender_diff, ax=axes[0, 0])
axes[0, 0].set_title('性别对总分的影响')
axes[0, 0].set_xlabel('性别')
axes[0, 0].set_ylabel('平均总分')

# 生源背景分析可视化
sns.barplot(x=origin_diff.index, y="综合", data=origin_diff, ax=axes[0, 1])
axes[0, 1].set_title('生源背景对总分的影响')
axes[0, 1].set_xlabel('生源背景')
axes[0, 1].set_ylabel('平均总分')

# 基因型分析可视化
sns.barplot(x=gene1_diff.index, y="综合", data=gene1_diff, ax=axes[0, 2])
axes[0, 2].set_title('基因型gene1对总分的影响')
axes[0, 2].set_xlabel('基因型gene1')
axes[0, 2].set_ylabel('平均总分')

sns.barplot(x=gene2_diff.index, y="综合", data=gene2_diff, ax=axes[1, 0])
axes[1, 0].set_title('基因型gene2对总分的影响')
axes[1, 0].set_xlabel('基因型gene2')
axes[1, 0].set_ylabel('平均总分')

# 生日与成绩的关系可视化
sns.barplot(x=birthday_diff.index, y="综合", data=birthday_diff, ax=axes[1, 1])
axes[1, 1].set_title('出生月份对总分的影响')
axes[1, 1].set_xlabel('出生月份')
axes[1, 1].set_ylabel('平均总分')

# 调整布局，防止标签重叠
plt.tight_layout()

plt.show()

# 相关性分析：分析不同科目成绩之间的相关性，以及这些科目成绩与总分的相关性。
# 回归分析：可以使用线性回归模型来探究哪些因素（如性别、生源、基因型等）对总分的影响最大。
# 分组分析：根据基因型、性别或生源进行更细致的分组，分析各组内成绩的分布情况。
# 年龄与成绩的关系：计算学生的年龄，并分析年龄与成绩之间的关系。
# 异常值检测：检查数据中是否存在异常值，这些异常值可能会对分析结果产生影响。

# 可视化基因型对成绩的影响
plt.figure(figsize=(10, 6))
sns.barplot(x='gene1', y='综合', data=data_df, ci=None)
plt.title('基因型gene1对总分的影响')
plt.xlabel('基因型gene1')
plt.ylabel('平均总分')
plt.show()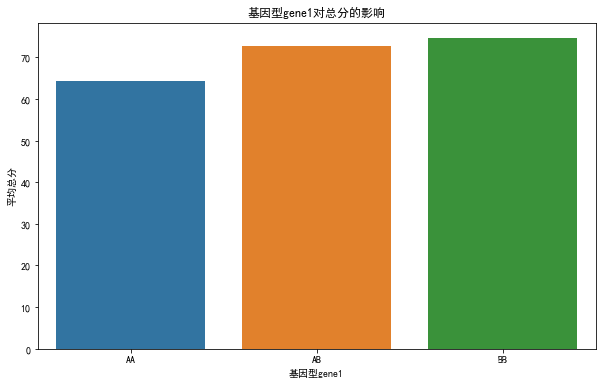

 

可视化相关性分析：

# 相关性分析
correlation = data_df[['名词', '填空', '简答', '计算', '综合', '年龄']].corr()
correlation

 

# 可视化相关性分析
plt.figure(figsize=(10, 6))
sns.heatmap(correlation, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('科目间及与总分的相关性')
plt.show()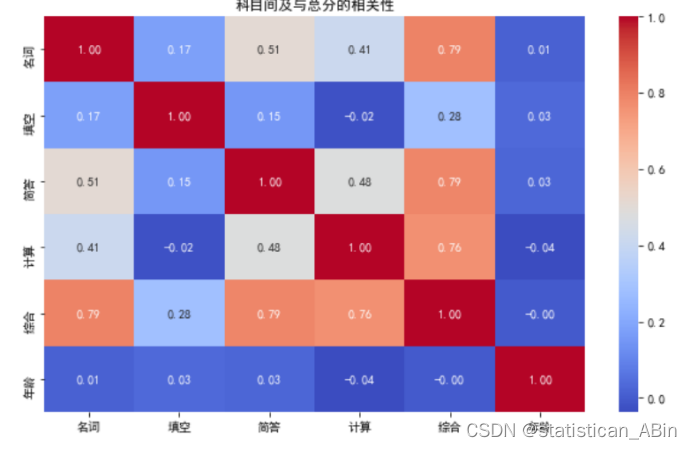

 科目间及与总分的相关性：展示了不同科目之间以及与总分之间的相关性。可见“名词”科目与总分的相关性最高。各科目间及与总分的相关性：科目“名词”与总分（综合）的相关性最高（0.79），其次是“简答”（0.79）和“计算”（0.76）。这表明这些科目对总分有较大影响。年龄与成绩的相关性：年龄与各科目成绩及总分的相关性都很低，说明年龄对成绩影响不大。

...

线性回归分析

由于涉及多个分类变量，此处使用ANOVA（方差分析）

anova_table = sm.stats.anova_lm(model, typ=2)
anova_table

	sum_sq	df	F	PR(>F)
C(性别)	10.522103	1.0	0.105609	7.453292e-01
C(生源)	0.292350	1.0	0.002934	9.568212e-01
C(gene1)	7366.159076	2.0	36.966647	9.589150e-16
C(gene2)	3889.908051	2.0	19.521281	6.652673e-09
Residual	52207.430611	524.0	NaN	NaN

基因型对成绩的影响显著：基因型（gene1和gene2）对总分有显著影响（P值远小于0.05）。

性别和生源对成绩的影响不显著：性别和生源对总分的影响不显著（P值大于0.05）。

三、总结

通过对硕士生考试成绩的综合分析，我们发现几个关键的发现。首先，性别和生源背景对学生成绩的影响不显著，而基因型在学生成绩上表现出显著的影响，特别是BB基因型的学生在总分上表现最好。其次，不同科目间的成绩相关性分析显示，“名词”科目与总分的相关性最高。此外，年龄对学生成绩的影响相对较小。最这些发现为理解硕士生的学术表现提供了重要的洞察，并为未来的教育研究和政策制定提供了数据支持。

创作不易，希望大家多多点赞收藏和评论！