🔒文章目录:
1.❤️❤️前言~🥳🎉🎉🎉
2. 二叉树的模拟——正文
2.1获取树中节点的个数
2.2获取叶子节点的个数
2.3获取第K层节点的个数
2.4获取二叉树的高度
2.5 检测值为value的元素是否存在
2.6 判断一棵树是不是完全二叉树
2.7遍历
2.7.1先序遍历
2.7.2中序遍历
2.7.3后序遍历
2.7.4层序遍历
3.二叉树的模拟——使用
4.特别说明
5.总结
1.❤️❤️前言~🥳🎉🎉🎉
Hello, Hello~ 亲爱的朋友们👋👋,这里是E绵绵呀✍️✍️。
如果你喜欢这篇文章,请别吝啬你的点赞❤️❤️和收藏📖📖。如果你对我的内容感兴趣,记得关注我👀👀以便不错过每一篇精彩。
当然,如果在阅读中发现任何问题或疑问,我非常欢迎你在评论区留言指正🗨️🗨️。让我们共同努力,一起进步!
加油,一起CHIN UP!💪💪
🔗个人主页:E绵绵的博客
📚所属专栏:1. JAVA知识点专栏
深入探索JAVA的核心概念与技术细节
2.JAVA题目练习
实战演练,巩固JAVA编程技能
3.c语言知识点专栏
揭示c语言的底层逻辑与高级特性
4.c语言题目练习
挑战自我,提升c语言编程能力
📘 持续更新中,敬请期待❤️❤️

2. 二叉树的模拟——正文
因为我们在上篇文章中已经对二叉树的模拟进行了一个前置的了解,还对二叉树的基础:遍历做了一个深度了解,那么现在我们就可以开始二叉树模拟的正文了,正文中我们将会模拟二叉树的基本方法和二叉树的四种遍历方式(前序,中序,后序,层序)。
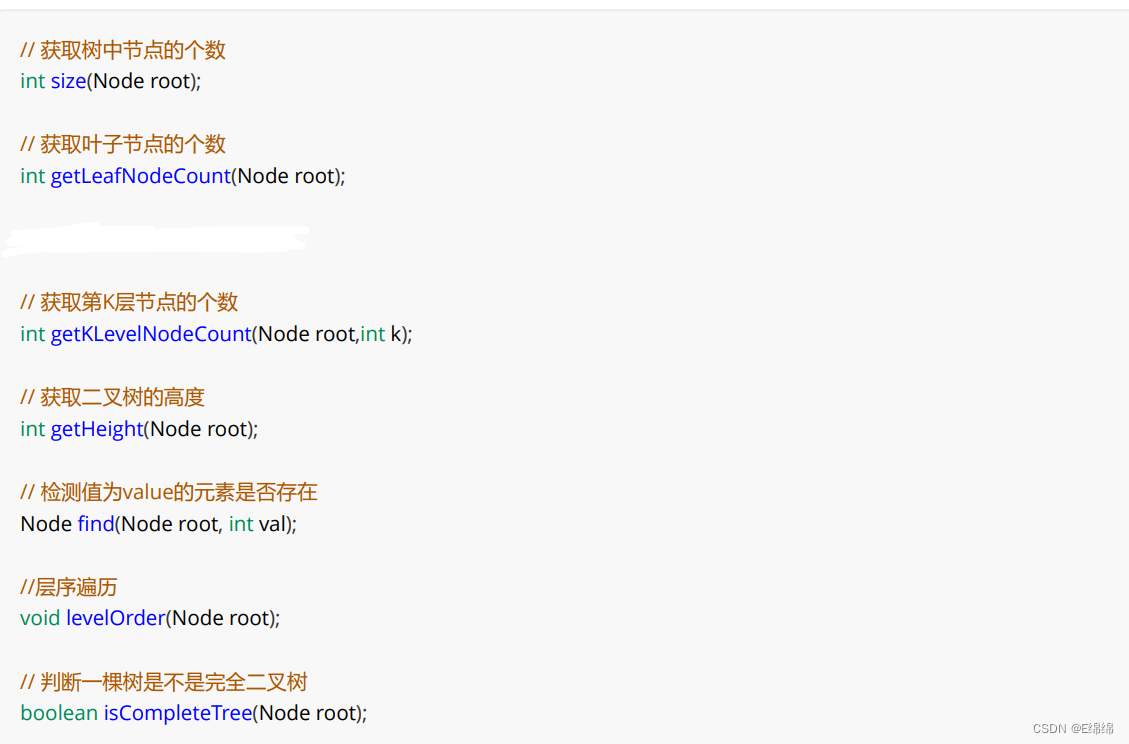
二叉树的基本方法如下:
因为在二叉树模拟的前置说明中我们已经创建好了一个二叉树,所以我们以它为操作对象去执行我们模拟的基本方法和四种遍历方式。
2.1获取树中节点的个数
我们采用递归的方式去实现。具体如下:
定义该函数的名称为 size,它接受一个参数 root,表示以该节点为根的二叉树。
首先定义一个变量 size,用于记录二叉树节点的个数,并初始化为 0。
然后判断 root 是否为 null,如果为 null,说明当前节点为空,直接返回 0。
否则,将 size 加 1,表示当前节点不为空,计入节点个数。
接着,对左子树和右子树进行递归调用 size 函数,分别计算左右子树中节点的个数。
最后将左右子树的节点个数加起来,并加上当前节点,即为整个二叉树的节点个数,返回 size。
int size(BTNode root) { int size = 0; if (root == null) return 0; size++; size = size + size(root.left); size = size + size(root.right); return size; }
2.2获取叶子节点的个数
注意:度为0的结点称为叶子结点。
我们设计一个函数名为
getLeafNodeCount,输入参数是二叉树的根节点root,返回值是整数类型,表示二叉树中叶子节点的数量。函数的实现思路是:如果二叉树为空,那么叶子节点数量为 0;否则,如果当前节点是叶子节点,则叶子节点数量加 1;接着递归地计算左子树和右子树中叶子节点的数量,并将它们相加作为最终的结果返回。
具体而言,该代码中首先定义了一个变量
size并初始化为 0。然后通过判断二叉树的根节点是否为空,来处理递归结束的情况。如果当前节点是叶子节点,则将size的值加 1;之后则递归地计算左右子树中叶子节点的数量,并将它们累加到size中。最后将size作为函数的返回值。
int getLeafNodeCount(BTNode root) { int size = 0; if (root == null) return 0; if ((root.left == null) && (root.right == null)) size++; size = size + getLeafNodeCount(root.left); size = size + getLeafNodeCount(root.right); return size; }
2.3获取第K层节点的个数
具体分析如下:
首先,定义一个函数getKLevelNodeCount,该函数需要传入两个参数:一个是二叉树的根节点root,另一个是需要统计节点个数的层数k。
接着,该函数定义了一个整型变量size并将其初始化为0。
然后,通过对root节点进行判断,若root为空,则返回0;若k为1,则返回1,此时只有根节点符合要求。
接下来,在左右子树中递归查找第k-1层的节点,而后将左右子树第k-1层的节点个数加起来,最终得到母树第k层的节点个数。
最后,返回size变量即可。
// 获取第K层节点的个数 int getKLevelNodeCount(BTNode root, int k) { int size = 0; if (root == null) return 0; if (k == 1) return 1; size = size + getKLevelNodeCount(root.left, k - 1); size = size + getKLevelNodeCount(root.right, k - 1); return size; }
2.4获取二叉树的高度
我们实现一个函数名为 getHeight,接受一个 BTNode 类型的参数 root,返回一个整型值表示二叉树的高度。其实现过程是通过递归方式计算根节点的左右子树高度的最大值,然后加上 1,即为整棵二叉树的高度。其中,当传入的二叉树为空时,直接返回 0。
值得注意的是,该代码使用了 Math.max 函数来比较左右子树高度的大小。这是 Java 内置的一个函数,可以用来获取两个数中的最大值。
int getHeight(BTNode root) { int height = 0; if (root == null) return 0; return Math.max(getHeight(root.left), getHeight(root.right)) + 1; }
2.5 检测值为value的元素是否存在
定义一个函数名为find,函数输入参数是一个二叉树的根节点
root和要查找的值val,返回值是该值所在的二叉树节点。具体实现方式是,先判断当前根节点是否为 null,若是则返回 null;若当前节点的值与目标值相等,则返回该节点;否则分别在左子树和右子树中递归查找目标值。如果左右子树都没有找到目标值,则返回 null,如果找到目标值则返回目标值所在的节点
// 检测值为value的元素是否存在 BTNode find(BTNode root, int val) { if (root == null) return null; if (root.value == val) return root; BTNode btNode1 = find(root.left, val); if (btNode1 != null) return btNode1; BTNode btNode2 = find(root.right, val); if (btNode2 != null) return btNode2; return null; }
2.6 判断一棵树是不是完全二叉树
其主要思路是通过 BFS(广度优先搜索)算法逐层遍历树,并在遇到第一个空节点时退出循环。然后再检查队列中是否还存在非空节点,若存在,则不是完全二叉树;若不存在,则是完全二叉树。具体解释可见下面分析:
函数名:isCompleteTree 返回值:boolean类型,表示是否为完全二叉树 参数:BTNode类型,表示二叉树的根节点
判断根节点是否为空,若为空,则直接返回 true,因为空树也可以看作是完全二叉树。
创建一个队列 queue,将根节点加入队列。
开始循环,当队列不为空时,循环体内部分以下操作: a. 取出队首元素 btNode1。 b. 若 btNode1 不为空,则将其左右儿子加入队列。 c. 若 btNode1 为空,则退出循环。
循环结束后,检查队列中是否还有非空节点。若有,则不是完全二叉树;若没有,则是完全二叉树。(我们能将null输入到队列里,同理队列也能输出null)
返回判断结果。
注意一个重要的点,之前栈和队列中讲过该知识点:栈和队列都允许存储null值。在栈和队列中,null值被视为一种有效的元素,因此可以被添加到栈和队列中,作为一个元素去存放。
我们如果不清楚该知识点的话这题是绝对想不到怎么解决的,毕竟该题是把null存储在队列中去解决问题的,如果你连null是否能存储在队列中都不清楚的话,又谈何去做该题。
//判断一棵树是不是完全二叉树 public boolean isCompleteTree(BTNode root) { if (root == null) return true; Queue<BTNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { BTNode btNode1 = queue.poll(); if (btNode1 != null) { queue.offer(btNode1.left); queue.offer(btNode1.right); } else { break; }} while(!queue.isEmpty()){ if(queue.peek()!=null) return false; else queue.poll(); } return true; }
2.7遍历
2.7.1先序遍历
二叉树的先序遍历 遍历顺序为:根节点 -> 左子树 -> 右子树。具体实现步骤如下:
- 判断二叉树节点是否为空,如果为空则直接返回。
- 输出当前节点的值。
- 递归调用前序遍历函数,遍历当前节点的左子树。
- 递归调用前序遍历函数,遍历当前节点的右子树。
//先序遍历 public void preorder(BTNode btNode) { if (btNode == null) return; System.out.print(btNode.value + " "); preorder(btNode.left); preorder(btNode.right); }
2.7.2中序遍历
中序遍历是二叉树遍历中的一种,它的遍历顺序是从左子树开始,到根节点,再到右子树。具体实现如下:
- 首先判断当前节点是否为 null,如果是则返回。
- 对当前节点的左子树进行递归 中序遍历。
- 遍历左子树完成后,输出当前节点的值。
- 对当前节点的右子树进行递归中序遍历。
//中序遍历 public void inorder(BTNode btNode) { if (btNode == null) return; inorder(btNode.left); System.out.print(btNode.value + " "); inorder(btNode.right); }
2.7.3后序遍历
后序遍历是指先访问左子树,再访问右子树,最后访问根节点的遍历方式。具体分析如下:
- 首先判断当前节点是否为空,如果为空则直接返回。
- 递归后序遍历 遍历当前节点的左子树。
- 递归后序遍历 遍历当前节点的右子树。
- 输出当前节点的值。
//后序遍历 public void postorder(BTNode btNode) { if (btNode == null) return; postorder(btNode.left); postorder(btNode.right); System.out.print(btNode.value + " "); }
2.7.4层序遍历
层序遍历是指从根节点开始,按照从上到下、从左到右的顺序依次访问二叉树中的每一个节点。具体分析如下:
首先判断二叉树的根节点是否为空,如果为空则直接返回。
创建一个队列(这里使用 Java 中的 LinkedList 实现),将根节点加入队列中。
当队列不为空时,重复以下操作:
a. 取出队头元素。
b. 输出队头元素的值。
c. 如果队头元素有左子节点,则将左子节点加入队列。
d. 如果队头元素有右子节点,则将右子节点加入队列。
当队列为空时,说明遍历完成,退出循环。
//层序遍历 public void levelOrder(BTNode btNode) { if (btNode == null) return; Queue<BTNode> queue = new LinkedList<>(); queue.offer(btNode); while (!queue.isEmpty()){ BTNode btNode1=queue.poll(); System.out.print(btNode1.value+" "); if(btNode1.left!=null) queue.offer(btNode1.left); if(btNode1.right!=null) queue.offer(btNode1.right); } }
3.二叉树的模拟——使用
以下是模拟的二叉树的全部代码
public class BinaryTree { static class BTNode { int value; BTNode left; BTNode right; public BTNode(int value){ this.value = value; } } public BTNode creatBinaryTree() { BTNode btNode1 = new BTNode(1); BTNode btNode2 = new BTNode(2); BTNode btNode3 = new BTNode(3); BTNode btNode4 = new BTNode(4); BTNode btNode5 = new BTNode(5); BTNode btNode6 = new BTNode(6); BTNode btNode7 = new BTNode(7); btNode1.left = btNode2; btNode1.right = btNode3; btNode2.left = btNode4; btNode2.right = btNode5; btNode3.right = btNode6; btNode5.left = btNode7; return btNode1; } //先序遍历 public void preorder(BTNode btNode) { if (btNode == null) return; System.out.print(btNode.value + " "); preorder(btNode.left); preorder(btNode.right); } //中序遍历 public void inorder(BTNode btNode) { if (btNode == null) return; inorder(btNode.left); System.out.print(btNode.value + " "); inorder(btNode.right); } //后序遍历 public void postorder(BTNode btNode) { if (btNode == null) return; postorder(btNode.left); postorder(btNode.right); System.out.print(btNode.value + " "); } //层序遍历 public void levelOrder(BTNode btNode) { if (btNode == null) return; Queue<BTNode> queue = new LinkedList<>(); queue.offer(btNode); while (!queue.isEmpty()){ BTNode btNode1=queue.poll(); System.out.print(btNode1.value+" "); if(btNode1.left!=null) queue.offer(btNode1.left); if(btNode1.right!=null) queue.offer(btNode1.right); } } //得出树的节点数量 int size(BTNode root) { int size = 0; if (root == null) return 0; size++; size = size + size(root.left); size = size + size(root.right); return size; } // 获取叶子节点的个数 int getLeafNodeCount(BTNode root) { int size = 0; if (root == null) return 0; if ((root.left == null) && (root.right == null)) size++; size = size + getLeafNodeCount(root.left); size = size + getLeafNodeCount(root.right); return size; } // 获取第K层节点的个数 int getKLevelNodeCount(BTNode root, int k) { int size = 0; if (root == null) return 0; if (k == 1) return 1; size = size + getKLevelNodeCount(root.left, k - 1); size = size + getKLevelNodeCount(root.right, k - 1); return size; } // 获取二叉树的高度 int getHeight(BTNode root) { int height = 0; if (root == null) return 0; return Math.max(getHeight(root.left), getHeight(root.right)) + 1; } // 检测值为value的元素是否存在 BTNode find(BTNode root, int val) { if (root == null) return null; if (root.value == val) return root; BTNode btNode1 = find(root.left, val); if (btNode1 != null) return btNode1; BTNode btNode2 = find(root.right, val); if (btNode2 != null) return btNode2; return null; } //判断一棵树是不是完全二叉树 public boolean isCompleteTree(BTNode root) { if (root == null) return true; Queue<BTNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { BTNode btNode1 = queue.poll(); if (btNode1 != null) { queue.offer(btNode1.left); queue.offer(btNode1.right); } else { break; }} while(!queue.isEmpty()){ if(queue.peek()!=null) return false; else queue.poll(); } return true; } }
我们将对上述模拟的二叉树进行使用,代码如下:
public class Test1 { public static void main(String[] args) { BinaryTree binaryTree=new BinaryTree(); BinaryTree.BTNode btNode=binaryTree.creatBinaryTree(); binaryTree.preorder(btNode); System.out.println(); binaryTree.inorder(btNode); System.out.println(); binaryTree.postorder(btNode); System.out.println(); binaryTree.levelOrder(btNode); System.out.println(); System.out.println(binaryTree.size(btNode));//节点个数 System.out.println(binaryTree.getLeafNodeCount(btNode));//叶子节点个数 System.out.println(binaryTree.getKLevelNodeCount(btNode, 3));//树的第三层的节点数 System.out.println(binaryTree.getHeight(btNode));//树的高度 System.out.println(binaryTree.size(binaryTree.find(btNode, 2))); //检测树中值为2的节点是否存在,如果存在,打印出该节点作为根节点时所代表的子树的节点数 System.out.println(binaryTree.isCompleteTree(btNode));//检测是否为完全二叉树 } }
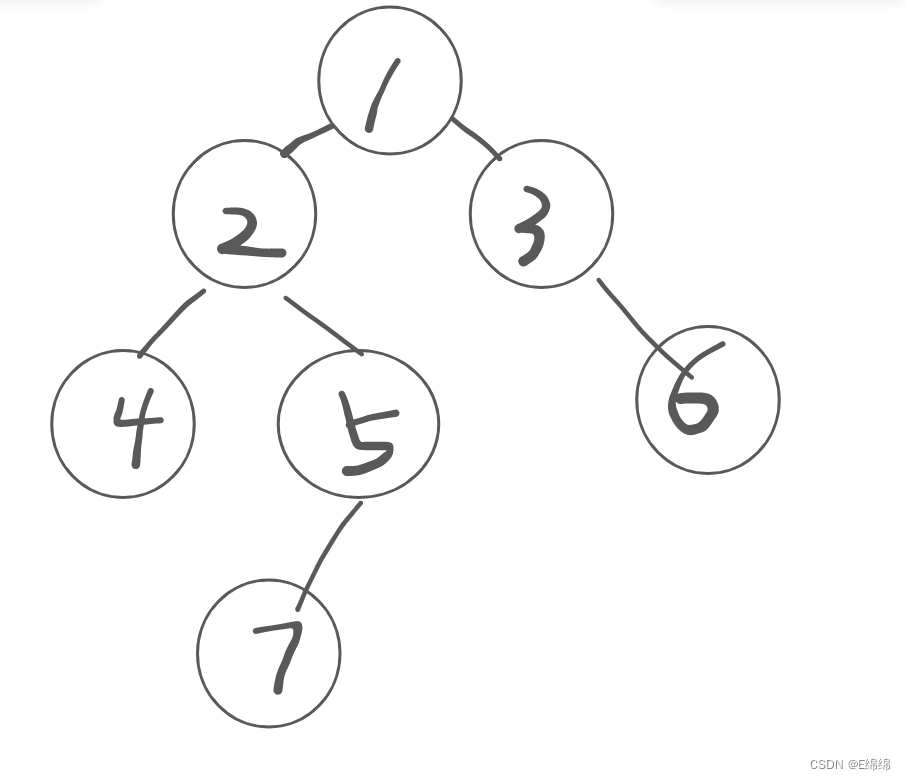
创建的树如下:
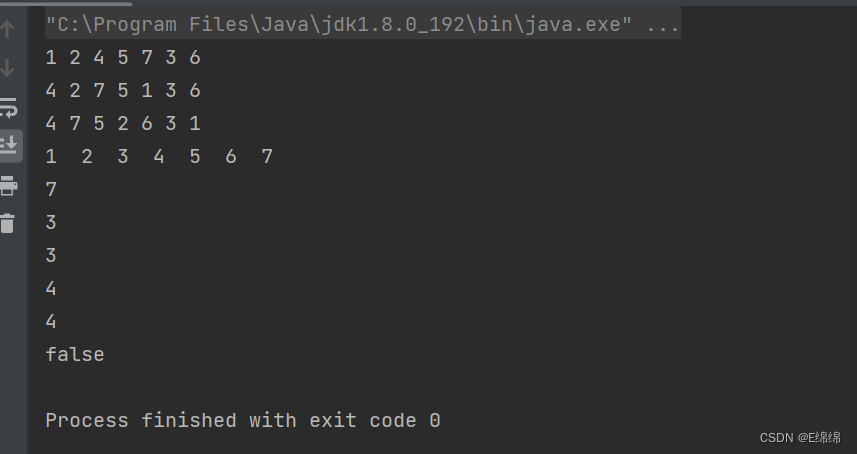
执行之后的结果如下:
我们发现其执行结果是如我们预料的一样,完全正确,所以二叉树的模拟就成功了,之后可以安心使用它了。
4.特别说明
对于我们上述模拟出来的二叉树,其在集合框架中并没有对应的类去实现。
那没有对应的类去实现它?我们为什么还要模拟呢?不白白浪费精力?
其实,我们之所以模拟出来这个二叉树,是为了打好基础。虽然我们模拟出来的这个二叉树并没有对应的类去实现,但在之后的学习中我们会学到堆,红黑树等,这些也都是二叉树,并且这些二叉树在集合框架中会有对应类去实现它们,所以我们现在模拟一个二叉树只是为了对二叉树有个更清晰的认知,为后序的堆,红黑树等其他一些二叉树的学习打好基础。
5.总结
所以这篇文章结束后,我们的二叉树的知识点就全讲解完了,下篇文章将会给大家带来二叉树的习题讲解。在此,我们诚挚地邀请各位大佬们为我们点赞、关注,并在评论区留下您宝贵的意见与建议。让我们共同学习,共同进步,为知识的海洋增添更多宝贵的财富!🎉🎉🎉❤️❤️💕💕🥳👏👏👏