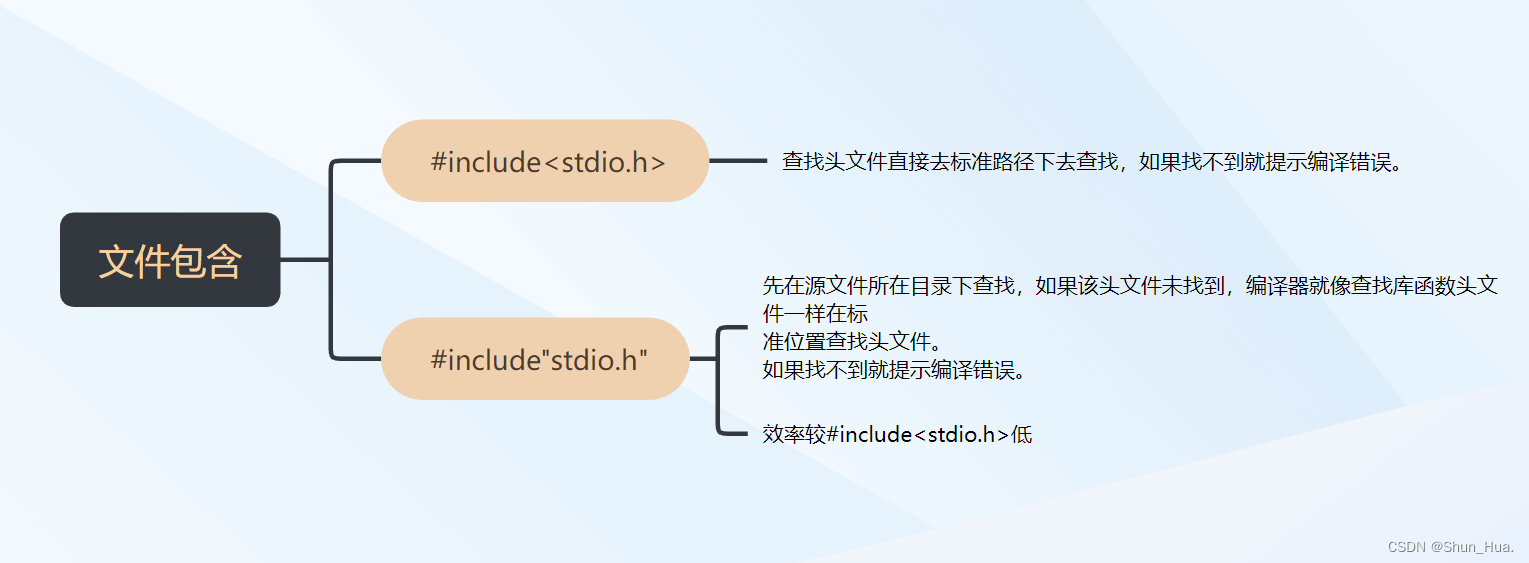
时间、空间复杂度比较
| 排序算法 | 平均时间复杂度 | 最差时间复杂度 | 空间复杂度 | 数据对象稳定性 |
|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(1) | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(1) | 数组不稳定、链表稳定 |
| 插入排序 | O(n2) | O(n2) | O(1) | 稳定 |
| 快速排序 | O(n*log2n) | O(n2) | O(log2n) | 不稳定 |
| 堆排序 | O(n*log2n) | O(n*log2n) | O(1) | 不稳定 |
| 归并排序 | O(n*log2n) | O(n*log2n) | O(n) | 稳定 |
| 希尔排序 | O(n*log2n) | O(n2) | O(1) | 不稳定 |
| 计数排序 | O(n+m) | O(n+m) | O(n+m) | 稳定 |
| 桶排序 | O(n) | O(n) | O(m) | 稳定 |
| 基数排序 | O(k*n) | O(n2) | 稳定 |
1 冒泡排序
1.首先我先说明一下冒泡排序的特点:
冒泡排序特点就是每一趟排序把最大的数字找出来并且同时放在最后。这样通过有限次的排序后,有限-无序-序列的数字就会被排序成有序序列。
2.那么冒泡算法是如何对数字进行排序的呢?
概念:以第一个数字为首,与后面第二个数字进行比较,如果第一个数字比第二个数字大,那么就把第一个数字与第二个数字的位置进行交换,否则该数字位置不变。然后第二个数字又与第三个数字进行比较,如果第二个数字大于第三个数字的话,则第二个数字与第三个数字进行位置交换......一直重复这样的操作,那么一趟排序下来就可以找出该序列的最大值了。(注意:每一趟排序的时候,之前所有排序出来的最大值不再参与本次排序)
下面是对:1 23 4 98 70 10 9 这一无序数字序列进行第一趟排序
①:1比23小,不调换位置。此时序列为:1 23 4 98 70 10 9
②:23比4大,调换位置。此时序列为:1 4 23 98 70 10 9(23与4调换了位置)
③:23比98小,不调换位置。此时序列为:1 4 23 98 70 10 9
④:98比70大,调换位置。此时序列为:1 4 23 70 98 10 9(98与70调换了位置)
⑤:98比10大,调换位置。此时序列为:1 4 23 70 10 98 9(98与10调换了位置)
⑥:98比9大,调换位置。此时序列为:1 4 23 70 10 9 98(98与9调换了位置)
如果觉得难以理解的朋友可以在草稿纸上画两个杯子,一号杯子装着所有的无序数字,二号杯子则为空。把每一趟排序出来的数字有序地放在二号杯子里面,然后对一号杯子重新排序。你会发现当你第二次对一号杯子进行排序的时候,所找出来的那个最大数字其实就是原来一号杯子所有数字的第二大数字。而第三次对一号杯子排序则找出来的是原有序列的第三大的数字。
算法思想:
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
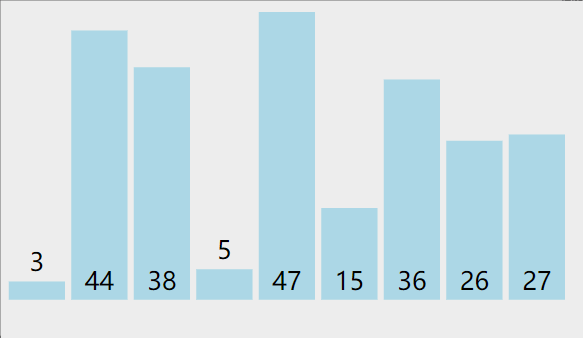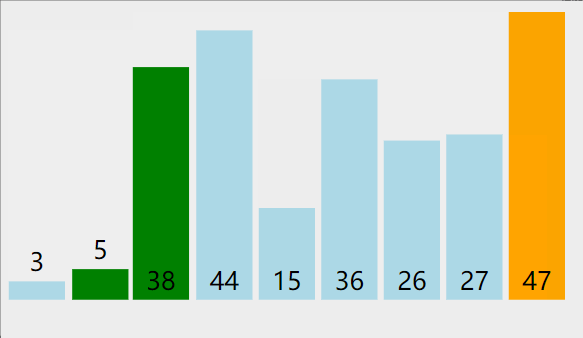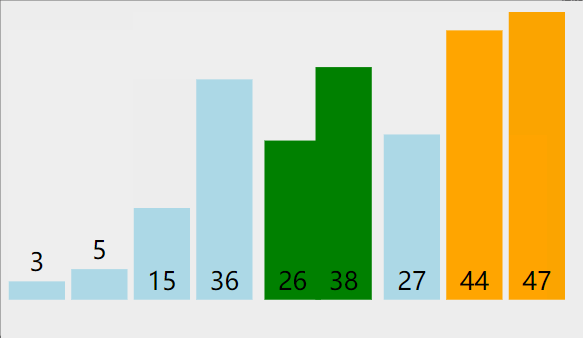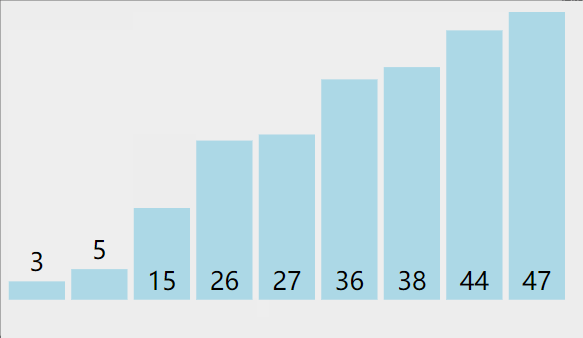
冒泡排序动图演示
代码:
void bubbleSort(int a[], int n)
{
for(int i =0 ; i< n-1; ++i)
{
for(int j = 0; j < n-i-1; ++j)
{
if(a[j] > a[j+1])
{
int tmp = a[j] ; //交换
a[j] = a[j+1] ;
a[j+1] = tmp;
}
}
}
}