本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记，详细视频参考
【电子科技大学】离散数学（上） 王丽杰
【电子科技大学】离散数学（下） 王丽杰
latex的离散数学写法参考： 离散数学与组合数学-01

离散数学公式
!符号 代码 含义
$\wedge$ \wedge 且
$\vee$ \vee 或
$\cap$ \cap 交
$\cup$ \cup 并
$\subseteq$ \subseteq 子集
$⊈$ \nsubseteq 不是子集
$\subset$ \subset 真子集
$\not\subset$ \not\subset 不是真子集
$\in$ \in 属于
$\notin$ \not\in 不属于
$\leftrightarrow$ \leftrightarrow 等价
$\iff$ \Leftrightarrow 等值
$\neg$ \neg或\lnot 非
$\mathbb{R}$ \mathbb{R} 实数集
$\mathbb{Z}$ \mathbb{Z} 整数集
$\varnothing$ \varnothing 空集
$\forall$ \forall 对任意的
$\exists$ \exists 存在
$\ge$ \geq大于等于
$\le$ \leq 小于等于

下标的输入命令是：$x_{内容}$ x_{内容}
上标的输入命令式：$x^2$ x^2
空格 \quad

$R/$ R\mkern-10.5mu/ 数值越大，斜杆越往字母左侧移动

离散数学与组合数学-03函数

3.1 函数基本概念

函数是数学中的一个基本概念, 它非常古老, 这个词出现于十七世纪下半叶,比关系理论早两个多世纪, 由伟大的数学家莱布尼兹提出, 他也与牛顿各自独立的发现了微积分的基本定理.
在高等数学中, 函数一般是在实数集的基础上来研究, 通常是连续或间断连续的函数. 在这里, 我们将函数看作是一种特殊的二元关系, 从离散量的角度讨论函数的定义, 运算和性质.
函数的概念在日常生活和计算机科学中非常重要. 例如, 各种高级程序语言中都大量的使用了函数。实际上, 计算机的任何输出都可看成是某些输入的函数.

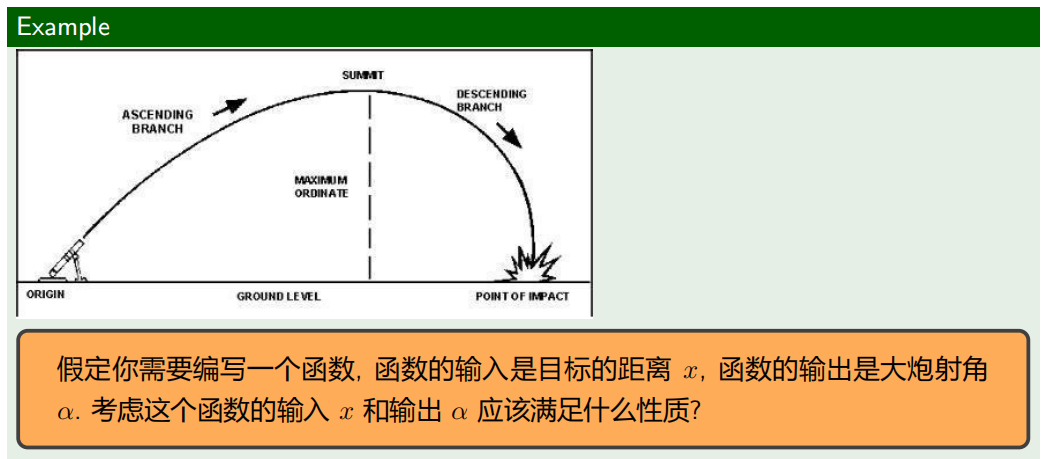
3.1.1 函数的定义

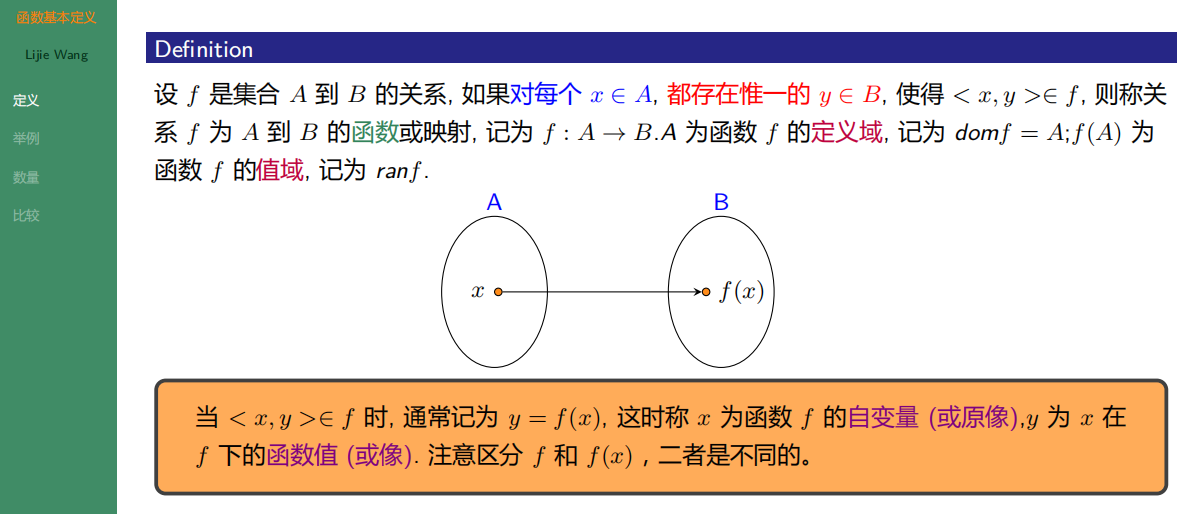
3.1.2 函数举例

3.1.3 函数的数量

3.1.4 关系与函数的差别

当 A 和 B 都是有限集合时, 函数和一般关系具有如下差别:
关系和函数的数量不同: 从 A 到 B 的不同关系有 $2^{|A|\times |B|}$ 个,
从 A 到 B 的不同函数却仅有 $|B{|}^{|A|}$ 个;
关系和函数的基数不同: 每一个关系的基数可以从零一直到 |A| × |B|, 每一个函数的基数都为 |A| 个;
关系和函数的第一元素存在差别: 关系的第一个元素可以相同, 函数的第一元素一定是互不相同的

3.2函数的类型

3.2.1 函数类型

设 f 是从集合 A 到 B 的函数,对任意 x1, x2 ∈ A, 如果 $x1=/x2$, 都有 $f(x1)=/f(x2)$, 则称 f 为从 A 到 B 的单射;
如果 ranf = B, 则称 f 为从 A 到 B 的满射;
如果 f 既是单射又是满射, 则称 f 为从 A 到 B 的双射.

3.2.2 函数类型的必要条件

3.2.3 函数类型的数学化描述

3.2.4 函数类型的证明

3.3 函数的运算

3.3.1 函数的复合运算

3.3.2 函数运算的保守性

3.3.3 函数的逆