【数据结构】二叉搜索树的实现

news2024/9/23 17:20:02

目录

一、二叉搜索树的概念

二、二叉搜索树的中序遍历用于排序+去重

三、二叉搜索树的查找

1、查找的非递归写法

2、查找的递归写法

四、二叉搜索树的插入

1、插入的非递归写法

2、插入的递归写法

五、二叉搜索树的删除

1、删除的非递归写法

2、删除的递归写法

六、二叉搜索树的使用场景

1、key搜索模型（节点存key）

2、key搜索模型整体代码

3、key/value搜索模型（节点既存key又存value）

4、key/value搜索模型整体代码

一、二叉搜索树的概念

二叉搜索树又称二叉排序树。

空树是二叉搜索树，如果一棵树不是空树，需要满足如下情况便可称其为二叉搜索树：

1、左子树上每一个键值均小于根节点；

2、右子树上每一个键值均大于根节点；

3、左右子树均为二叉搜索树。

template <class K>
struct BSTreeNode//用于生成二叉搜索树的节点
{
    BSTreeNode(const K& key)
    :_left(nullptr)
    ,_right(nullptr)
    ,_key(key)
    {}
    BSTreeNode<K>* _left;
    BSTreeNode<K>* _right;
    K _key;
};
template <class K>
struct BSTree//表示整颗二叉搜索树
{
    typedef BSTreeNode<K> Node;
    BSTree()
    :_root(nullptr)
    {}
private:
	Node* _root;
};

二、二叉搜索树的中序遍历用于排序+去重

通过上面那张图不难发现，用二叉搜索树走个中序，就是升序+去重排序，这也是二叉搜索树又被称为二叉排序树的原因。

使用InOrder调用_InOrder的原因是类外面传参传不了私有的_root，所以采用多套一层的方法。

//中序遍历
void _InOrder(Node* _root)
{
    if (_root == nullptr)
    {
        return;
    }
    _InOrder(_root->_left);
    std::cout << _root->_key << " ";
    _InOrder(_root->_right);
}
void InOrder()//因为外部取不到_root,所以这里套了一层调用函数
{
    _InOrder(_root);
    std::cout << std::endl;
}

三、二叉搜索树的查找

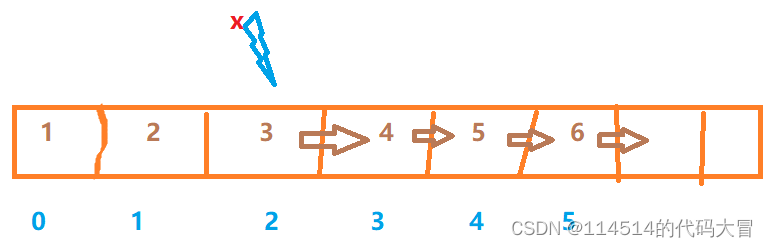
对于任意一颗二叉搜索树，最坏的查找次数是数的高度次，时间复杂度O(N)。

如果全国14亿人的身份证号按照完全二叉搜索树进行排列，2^(30)<14亿<2^(31)

，也就是说，在14亿人口中，我找到你最坏的情况下仅需要找31次。

可以看到，二叉搜索树针对满二叉树、完全二叉树这种结构平衡的树时，查找效率为O（logN），但是二叉搜索树如果处理有序或接近有序的数据，可能出现上图单子树的情况，大大降低了查找效率，所以它并不是一个很成熟的数据结构，需要平衡二叉树和红黑树对该缺陷进行弥补。（手撕平衡二叉树和红黑树博客尽量一个月左右补上）

1、查找的非递归写法

bool Find(const K& key)
{
    Node* cur = _root;
    while (cur)
    {
        if (cur->_key < key)
        {
            cur = cur->_right;
        }
        else if (cur->_key > key)
        {
            cur = cur->_left;
        }
        else//说明找到了
            return true;
    }
	return false;
}

根据二叉搜索树的性质，左树均小于根，右树均大于根，进行查找。

2、查找的递归写法

Node* _FindR(Node* root,const K& key)
{
    if (root == nullptr)
        return nullptr;
    if (root->_key < key)
    {
        return _FindR(root->_right, key);
    }
    else if (root->_key > key)
    {
        return _FindR(root->_left, key);
    }
    else
        return root;
}
bool FindR(const K& key)
{
    return _FindR(_root, key) == nullptr ? false : true;
}

四、二叉搜索树的插入

二叉搜索树的插入需要考虑插入后，需要维持二叉搜索树的形态。

1、插入的非递归写法

bool Insert(const K& key)
{
    if (_root == nullptr)
    {
        _root = new Node(key);//BSTreeNode对象中存放key值，构造一个二叉搜索树节点 
    }
    else
    {
        Node* parent = nullptr;
        Node* cur = _root;
        //cur一直走，走到要插入的位置
        while (cur)
        {
            parent = cur;
            if (cur->_key < key)
            {
                cur = cur->_right;
            }
            else if (cur->_key > key)
            {
                cur = cur->_left;
            }
            else//说明数字重复，插入失败
                return false;
        }
        cur = new Node(key);
        //判断插入节点放在parent节点的左子树还是右子树
        if (parent->_key < key)
        {
            parent->_right = cur;
        }
        else
        {
            parent->_left = cur;
        }
    }
    return true;
}

1、如果根是空，插入的节点就是新的根；

2、如果根不为空，就先根据二叉搜索树的性质找到该节点要插入的位置，如果路上遇到相同的数，插入失败；

3、再判断一下，是要插入父亲的左边还是右边即可。

2、插入的递归写法

bool _InsertR(Node*& root, const K& key)//形参是root的引用
{
    if (root == nullptr)
    {
        root = new Node(key);//因为root是父节点左/右孩子的别名，直接修改别名，链接关系存在，不用考虑父子节点连接关系
        return true;
    }
    if (root->_key < key)
        return _InsertR(root->_right, key);//看到这个root->_right没，它是下一层root的别名
    else if (root->_key > key)
        return _InsertR(root->_left, key);//看到这个root->_left没，它是下一层root的别名
    else//说明相等，插入失败
        return false;
}
bool InsertR(const K& key)
{
    return _InsertR(_root, key);
}

递归写法巧就巧在形参是指针的引用，例如我现在要插入9，下层的root是上一层root->_left的别名， 下层root = new Node(key);即为上一层root->_left=new Node(key);这样插入节点就自动和父节点连接上了。

五、二叉搜索树的删除

二叉搜索树的节点进行删除后，同样需要维持二叉搜索树的形态。

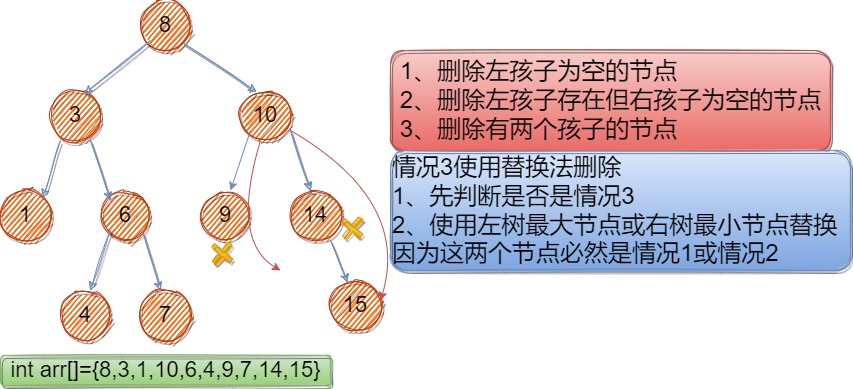
二叉搜索树的删除无非是三种情况：

1、删除的非递归写法

bool Erase(const K& key)
{
    Node* parent = nullptr;
    Node* cur = _root;
    //找到要删除的节点
    while (cur)
    {
        if (cur->_key < key)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_key > key)
        {
            parent = cur;
            cur = cur->_left;
        }
        else//说明找到要删除的节点了
        {
            //开始分析三种情况
            if (cur->_left == nullptr)//被删除节点左孩子为空。
            {
                if (cur == _root)//需要判断cur等于根节点的情况，否则else中parent空指针解引用了
                {
                    _root = _root->_right;
                }
                else
                {
                    if (parent->_left == cur)//确定cur是parent的左还是右，再进行“托孤”
                        parent->_left = cur->_right;
                    else
                        parent->_right = cur->_right;
                }	
                delete cur;
            }
            else if (cur->_right == nullptr)//被删除节点左孩子不为空,右孩子为空
            {
                if (cur == _root)
                {
                    _root = _root->_left;
                }
                else
                {
                    if (parent->_left == cur)
                        parent->_left = cur->_left;
                    else
                        parent->_right = cur->_left;
                }	
                delete cur;
            }
            else//被删除节点左右孩子均不为空
            {
                //左右孩子均不为空，就需要左子树的最大值或右子树的最小值选出来当新根（对被删除节点进行替换）
                Node* rightMin = cur->_right;//这里选用右树的最小值进行更换
                Node* rightMinParent = cur;
                while (rightMin->_left!=nullptr)//因为找最小值，不停找左树即可
                {
                    rightMinParent = rightMin;
                    rightMin = rightMin->_left;
                }
                //std::swap(cur->_key, rightMin->key);//用std的交换对自定义类型可能比较慢
                cur->_key = rightMin->_key;//还是用赋值好一点，即使是自定义类型，肯定有写赋值重载
                //rightMin的左节点必为空，判断父节点的链接方式即可
                if (rightMinParent->_left == rightMin)//两种情况，第一种如上方图删除8，实际干掉9位置，需要将10的左连至9的右
                    rightMinParent->_left = rightMin->_right;
                else if (rightMinParent->_right == rightMin)//第二种如上方图删除10，实际干掉14，需要将10的右连至14的右
                    rightMinParent->_right = rightMin->_right;
                delete rightMin;
            }
            return true;
        }
    }
    return false;
}

1、先通过二叉搜索树的性质找到要删除的节点；

2、找到需要删除的节点后，分三种情况进行讨论：

一、被删除节点的左孩子为空，除了cur等于根节点情况下，其他情况下，父节点的孩子指针由指向被删除节点转为指向被删除节点的右孩子。（如图删除9和14）

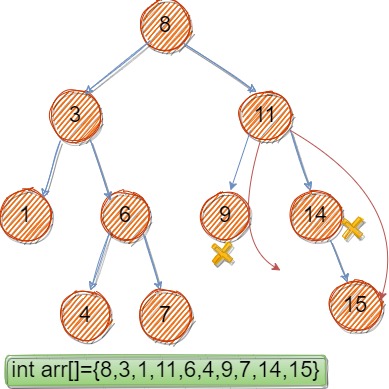
二、被删除节点的左孩子存在但右孩子为空，除了cur等于根节点情况下，其他情况下，父节点的孩子指针由指向被删除节点转为指向被删除节点的左孩子。（如图删除9）

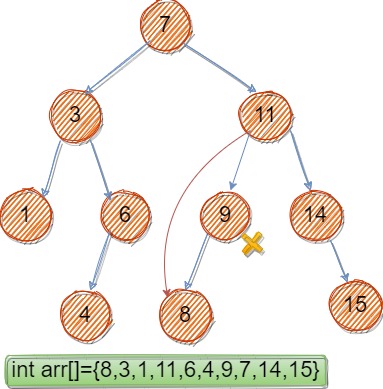
三、被删除的节点均不为空，可以选用左树最大节点或者右树最小节点对被删除节点进行值替换，问题转化为第一种或第二种情况。（详见代码注释）

2、删除的递归写法

bool _EarseR(Node*& root, const K& key)//形参给了引用，意义同插入的递归写法
{
    if (root == nullptr)
    {
        return false;
    }
    if (root->_key < key)
        return _EarseR(root->_right, key);
    else if (root->_key > key)
        return _EarseR(root->_left, key);
    else//说明找到了要删除的节点,无需考虑root的父亲为空
    {
        Node* del = root;
        if (root->_left == nullptr)//被删除节点的左为空
            root = root->_right;//让root连接root的右树，因为是引用，所以父节点和root是连接的
        else if (root->_right == nullptr)//被删除节点左不为空但右为空
            root = root->_left;
        else//root左右子树均不为空
        {
            Node* rightMin = root->_right;
            while (rightMin->_left!=nullptr)//找到被删除节点的右树最小节点 
            {
                rightMin = rightMin->_left;
            }
            root->_key = rightMin->_key;//找到了交换key
            //对子树进行递归删除
            return _EarseR(root->_right, rightMin->_key);//return表示子树进行删除，结束掉递归
        }
        delete del;
        return true;
    }
}
bool EraseR(const K& key)
{
    return _EarseR(_root, key);
}

找到节点后，同样需要分三种情况讨论。

1、被删除节点左树为空；

2、被删除节点左树不为空但右树为空；

3、被删除节点左右子树均不为空。

六、二叉搜索树的使用场景

1、key搜索模型（节点存key）

key搜索模型只用key作关键码，结构中只需存key，key即为需要搜索到的值。

例如对英语单词拼写的检查，可以将词库中的所有单词存入二叉搜索树，通过二叉搜索树中检索单词是否存在，达到拼写报错目的。

2、key搜索模型整体代码

template <class K>
struct BSTreeNode
{
	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;
};
template <class K>
struct BSTree
{
	typedef BSTreeNode<K> Node;
	BSTree()
		:_root(nullptr)
	{}
	//插入节点
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);//BSTreeNode对象中存放key值 
		}
		else
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				parent = cur;
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else//说明数字重复
					return false;
			}
			cur = new Node(key);
			//判断插入节点放在parent节点的左子树还是右子树
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
		}
		return true;
	}
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}
	//中序遍历
	void InOrder()//因为外部取不到_root,所以这里套了一层调用函数
	{
		_InOrder(_root);
		std::cout << std::endl;
	}
	//查找
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
				return true;
		}
		return false;
	}
	bool FindR(const K& key)
	{
		return _FindR(_root, key) == nullptr ? false : true;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		//找到要删除的节点
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else//说明找到要删除的节点了
			{
				//开始分析三种情况
				if (cur->_left == nullptr)//被删除节点左孩子为空。
				{
					if (cur == _root)//需要判断cur等于根节点的情况，否则else中parent空指针解引用了
					{
						_root = _root->_right;
					}
					else
					{
						if (parent->_left == cur)//确定cur是parent的左还是右，再进行“托孤”
							parent->_left = cur->_right;
						else
							parent->_right = cur->_right;
					}	
					delete cur;
				}
				else if (cur->_right == nullptr)//被删除节点左孩子不为空,右孩子为空
				{
					if (cur == _root)
					{
						_root = _root->_left;
					}
					else
					{
						if (parent->_left == cur)
							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}	
					delete cur;
				}
				else//被删除节点左右孩子均不为空
				{
					//左右孩子均不为空，就需要左子树的最大值或右子树的最小值选出来当新根
					Node* rightMin = cur->_right;//这里选用右树的最小值进行更换
					Node* rightMinParent = cur;
					while (rightMin->_left!=nullptr)
					{
						rightMinParent = rightMin;
						rightMin = rightMin->_left;
					}
					//std::swap(cur->_key, rightMin->key);//用std的交换对自定义类型可能比较慢
					cur->_key = rightMin->_key;//还是用赋值好一点，即使是自定义类型，肯定有写赋值重载
					if (rightMinParent->_left == rightMin)//两种情况，第一种如图删除8，实际干掉9位置，需要将10的左连至9的右
						rightMinParent->_left = rightMin->_right;
					else if (rightMinParent->_right == rightMin)//第二种如图删除10，实际干掉14，需要将10的右连至14的右
						rightMinParent->_right = rightMin->_right;
					delete rightMin;
				}
				return true;
			}
		}
		return false;
	}
	bool EraseR(const K& key)
	{
		return _EarseR(_root, key);
	}
private:
	Node* _root;
	void _InOrder(Node* _root)
	{
		if (_root == nullptr)
		{
			return;
		}
		_InOrder(_root->_left);
		std::cout << _root->_key << " ";
		_InOrder(_root->_right);
	}
	Node* _FindR(Node* root,const K& key)
	{
		if (root == nullptr)
			return nullptr;
		if (root->_key < key)
		{
			return _FindR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _FindR(root->_left, key);
		}
		else
			return root;
	}
	bool _InsertR(Node*& root, const K& key)//形参是root的引用
	{
		if (root == nullptr)
		{
			root = new Node(key);//因为root是父节点左/右孩子的别名，直接修改别名，链接关系存在，不用考虑父子节点连接关系
			return true;
		}
		if (root->_key < key)
			return _InsertR(root->_right, key);
		else if (root->_key > key)
			return _InsertR(root->_left, key);
		else
			return false;
	}
	bool _EarseR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			return false;
		}
		if (root->_key < key)
			return _EarseR(root->_right, key);
		else if (root->_key > key)
			return _EarseR(root->_left, key);
		else//说明找到了要删除的节点,无需考虑root的父亲为空
		{
			Node* del = root;
			if (root->_left == nullptr)
				root = root->_right;
			else if (root->_right == nullptr)
				root = root->_left;
			else//root左右子树均不为空
			{
				Node* rightMin = root->_right;
				while (rightMin->_left!=nullptr)//找到右树最小节点 
				{
					rightMin = rightMin->_left;
				}
				root->_key = rightMin->_key;
				return _EarseR(root->_right, rightMin->_key);//return表示子树进行删除，结束掉递归
			}
			delete del;
			return true;
		}
	}
};

3、key/value搜索模型（节点既存key又存value）

key/value搜索模型指每一个key值，都有与之对应的value值，例如英汉互译，一个英文单词可以对应一个翻译字符串。该模型还可以用于统计相同内容出现次数。（举例代码见下方测试函数。）

4、key/value搜索模型整体代码

namespace KV
{
	template <class K,class V>
	struct BSTreeNode
	{
		BSTreeNode(const K& key,const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			,_value(value)
		{}
		BSTreeNode<K,V>* _left;
		BSTreeNode<K,V>* _right;
		K _key;
		V _value;
	};
	template <class K,class V>
	struct BSTree
	{
		typedef BSTreeNode<K,V> Node;
		BSTree()
			:_root(nullptr)
		{}
		//插入节点
		bool Insert(const K& key,const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key,value);//BSTreeNode对象中存放key值 
			}
			else
			{
				Node* parent = nullptr;
				Node* cur = _root;
				while (cur)
				{
					parent = cur;
					if (cur->_key < key)
					{
						cur = cur->_right;
					}
					else if (cur->_key > key)
					{
						cur = cur->_left;
					}
					else//说明数字重复
						return false;
				}
				cur = new Node(key, value);
				//判断插入节点放在parent节点的左子树还是右子树
				if (parent->_key < key)
				{
					parent->_right = cur;
				}
				else
				{
					parent->_left = cur;
				}
			}
			return true;
		}
		bool InsertR(const K& key,const V& value)
		{
			return _InsertR(_root, key, value);
		}
		//中序遍历
		void InOrder()//因为外部取不到_root,所以这里套了一层调用函数
		{
			_InOrder(_root);
			std::cout << std::endl;
		}
		//查找
		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
					return cur;
			}
			return nullptr;
		}
		Node* FindR(const K& key)
		{
			return _FindR(_root, key);
		}
		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			//找到要删除的节点
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else//说明找到要删除的节点了
				{
					//开始分析三种情况
					if (cur->_left == nullptr)//被删除节点左孩子为空。
					{
						if (cur == _root)//需要判断cur等于根节点的情况，否则else中parent空指针解引用了
						{
							_root = _root->_right;
						}
						else
						{
							if (parent->_left == cur)//确定cur是parent的左还是右，再进行“托孤”
								parent->_left = cur->_right;
							else
								parent->_right = cur->_right;
						}
						delete cur;
					}
					else if (cur->_right == nullptr)//被删除节点左孩子不为空,右孩子为空
					{
						if (cur == _root)
						{
							_root = _root->_left;
						}
						else
						{
							if (parent->_left == cur)
								parent->_left = cur->_left;
							else
								parent->_right = cur->_left;
						}
						delete cur;
					}
					else//被删除节点左右孩子均不为空
					{
						//左右孩子均不为空，就需要左子树的最大值或右子树的最小值选出来当新根
						Node* rightMin = cur->_right;//这里选用右树的最小值进行更换
						Node* rightMinParent = cur;
						while (rightMin->_left != nullptr)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						//std::swap(cur->_key, rightMin->key);//用std的交换对自定义类型可能比较慢
						cur->_key = rightMin->_key;//还是用赋值好一点，即使是自定义类型，肯定有写赋值重载
						cur->_value = rightMin->_value;
						if (rightMinParent->_left == rightMin)//两种情况，第一种如图删除8，实际干掉9位置，需要将10的左连至9的右
							rightMinParent->_left = rightMin->_right;
						else if (rightMinParent->_right == rightMin)//第二种如图删除10，实际干掉14，需要将10的右连至14的右
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
					}
					return true;
				}
			}
			return false;
		}
		bool EraseR(const K& key)
		{
			return _EarseR(_root, key);
		}
	private:
		Node* _root;
		void _InOrder(Node* _root)
		{
			if (_root == nullptr)
			{
				return;
			}
			_InOrder(_root->_left);
			std::cout << _root->_key << " "<<_root->_value;
			_InOrder(_root->_right);
		}
		Node* _FindR(Node* root, const K& key)
		{
			if (root == nullptr)
				return nullptr;
			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
				return root;
		}
		bool _InsertR(Node*& root, const K& key, const V& value)//形参是root的引用
		{
			if (root == nullptr)
			{
				root = new Node(key,value);//因为root是父节点左/右孩子的别名，直接修改别名，链接关系存在，不用考虑父子节点连接关系
				return true;
			}
			if (root->_key < key)
				return _InsertR(root->_right, key，value);
			else if (root->_key > key)
				return _InsertR(root->_left, key，value);
			else
				return false;
		}
		bool _EarseR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}
			if (root->_key < key)
				return _EarseR(root->_right, key);
			else if (root->_key > key)
				return _EarseR(root->_left, key);
			else//说明找到了要删除的节点,无需考虑root的父亲为空
			{
				Node* del = root;
				if (root->_left == nullptr)
					root = root->_right;
				else if (root->_right == nullptr)
					root = root->_left;
				else//root左右子树均不为空
				{
					Node* rightMin = root->_right;
					while (rightMin->_left != nullptr)//找到右树最小节点 
					{
						rightMin = rightMin->_left;
					}
					root->_key = rightMin->_key;
					root->_value = rightMin->_value;
					return _EarseR(root->_right, rightMin->_key);//return表示子树进行删除，结束掉递归
				}
				delete del;
				return true;
			}
		}
	};
}
void testKV1()//中英互译
{
	KV::BSTree<std::string, std::string> dic;
	dic.Insert("data", "数据");
	dic.Insert("algorithm", "算法");
	dic.Insert("map", "地图、映射");
	dic.Insert("Linux", "一款开源免费的操作系统");
	std::string str;
	while (std::cin >> str)
	{
		KV::BSTreeNode<std::string, std::string>* ret = dic.Find(str);
		if (ret != nullptr)
		{
			std::cout << "中文翻译：" << ret->_value << std::endl;
		}
		else
			std::cout << "查找失败！" << std::endl;
	}
}
void testKV2()//用于统计次数
{
	std::string arr[] = { "数学", "语文", "数学", "语文", "数学", 
		"数学", "英语","数学", "英语", "数学", "英语" };
	KV::BSTree<std::string, int> count;
	for (auto& e : arr)
	{
		KV::BSTreeNode<std::string, int>* ret = count.Find(e);
		if (ret != nullptr)
		{
			ret->_value++;
		}
		else
		{
			count.Insert(e,1);
		}
	}
	count.InOrder();
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/176672.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

autojs模仿QQ长按弹窗菜单(二)

autojs模仿QQ长按弹窗菜单(二)

牙叔教程 简单易懂 上一节讲了列表和长按事件 autojs模仿QQ长按弹窗菜单 今天讲弹窗菜单 由粗到细, 自顶向下的写代码 我们现在要修改的文件是showMenuWindow.js function showMenuWindow(view) {let popMenuWindow ui.inflateXml(view.getContext(),<column><bu…
阅读更多...
基于双层优化的微电网系统规划设计方法（Matlab代码实现）

基于双层优化的微电网系统规划设计方法（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
机制设计原理与应用(一)机制设计基础

机制设计原理与应用(一)机制设计基础

什么是机制设计&#xff1f; 微观经济学和CS /EE的交叉学科。它采用了一种工程方法来设计激励机制&#xff0c;以实现战略环境中不完全信息的预期目标。机制设计具有广泛的应用,特别是在资源管理方面。 文章目录1 机制设计的基础1.1 简介1.2 机制设计与博弈及优化的关系1.3 机…
阅读更多...
手撕Pytorch源码#4.Dataset类 part4

手撕Pytorch源码#4.Dataset类 part4

写在前面手撕Pytorch源码系列目的&#xff1a;通过手撕源码复习了解高级python语法熟悉对pytorch框架的掌握在每一类完成源码分析后&#xff0c;会与常规深度学习训练脚本进行对照本系列预计先手撕python层源码&#xff0c;再进一步手撕c源码版本信息python&#xff1a;3.6.13p…
阅读更多...
大数据之HBase集群搭建

大数据之HBase集群搭建

文章目录前言一、上传并解压HBase安装包二、修改HBase配置文件&#xff08;一&#xff09;hbase-env.sh&#xff08;二&#xff09;hbase-site.xml三、配置环境变量四、复制jar包到lib文件夹五、修改regionservers文件六、分发安装包和配置文件七、启动Hbase八、验证HBase是否启…
阅读更多...
尚硅谷前端ES6-ES11

尚硅谷前端ES6-ES11

ECMAScript 是由 Ecma 国际通过 ECMA-262 标准化得脚本程序设计语言。 1.let变量声明以及变量声明特性 <body><script>//let的声明let a , b10;//特性1&#xff1a;变量不能重复声明&#xff0c;避免命名污染// let star "罗翔"// let star "张…
阅读更多...
Java | 浅谈多态中的向上转型与向下转型

Java | 浅谈多态中的向上转型与向下转型

文章目录&#x1f333;向上转型&#x1f4d5;概念明细&#x1f4aa;使用场景1&#xff1a;直接赋值&#x1f4aa;使用场景2&#xff1a;方法传参&#x1f4aa;使用场景3&#xff1a;方法返回&#x1f4aa;向上转型的优缺点&#x1f333;向下转型&#x1f529;向下转型解决【调用…
阅读更多...
程序员拯救了一次地球

程序员拯救了一次地球

流浪地球2&#xff1a;程序员拯救了一次地球 顺便给我们讲了一个道理&#xff1a; 人类会谋划未来&#xff0c; 但关键的一步是靠勇气迈出去的 趣讲大白话&#xff1a;算得好不如胆量好 *********** 电影工业的皇冠是特效 国产电影的特效进步不小 时时刻刻&#xff0c;分分秒秒…
阅读更多...
用户画像计算更新

用户画像计算更新

3.1 用户画像计算更新 目标 目标 知道用户画像建立的流程应用 无 3.1.1 为什么要进行用户画像 要做精准推送同样可以使用多种推荐算法&#xff0c;例如&#xff1a;基于用户协同推荐、基于内容协同的推荐等其他的推荐方式&#xff0c;但是以上方式多是基于相似进行推荐。而构…
阅读更多...
ROS移动机器人——ROS基础知识与编程

ROS移动机器人——ROS基础知识与编程

此文章基于冰达机器人进行笔记整理&#xff0c;使用的环境为其配套环境&#xff0c;可结合之前的ROS&#xff0c;赵虚左老师的文章结合进行观看&#xff0c;后期也会进行整合 1. ROS安装 &#xff08;1&#xff09;配置ubuntu的软件和更新&#xff0c;允许安装不经认证的软件…
阅读更多...
JS手动触发PWA安装窗口

JS手动触发PWA安装窗口

✅作者简介&#xff1a;人工智能专业本科在读&#xff0c;喜欢计算机与编程&#xff0c;写博客记录自己的学习历程。 &#x1f34e;个人主页&#xff1a;小嗷犬的博客 &#x1f34a;个人信条&#xff1a;为天地立心&#xff0c;为生民立命&#xff0c;为往圣继绝学&#xff0c;…
阅读更多...
仿写Dubbo-初识Dubbo

仿写Dubbo-初识Dubbo

概念 Dubbo 在Dubbo官网介绍到&#xff0c;Apache Dubbo 是一款 RPC 服务开发框架&#xff0c;用于解决微服务架构下的服务治理与通信问题。 RPC RPC&#xff08;Remote Procedure Call&#xff09;远程过程调用协议&#xff0c;一种通过网络从远程计算机上请求服务&#xff0c…
阅读更多...
【Android】手机安装Termux运行nodejs学习Javascript编程入门

【Android】手机安装Termux运行nodejs学习Javascript编程入门

Termux 是运行在Android手机上的一个 Linux 终端模拟器&#xff0c;干什么都要输入命令执行&#xff0c;不像 Windows 操作系统桌面用鼠标点点点&#xff0c;这里主要介绍用它来学习Javascript编程入门&#xff0c;当然&#xff0c;这和小时候学过的C语言编程课入门一样的&…
阅读更多...
C语言之程序设计概述

C语言之程序设计概述

1.1.1 程序的概念 程序&#xff1a;算法 数据结构 程序设计方法 语言工具和环境数据结构&#xff1a;数据的类型和数据的组织方式算法&#xff1a;对数据操作的方法和步骤 1.1.2 程序设计语言的种类 第一代语言&#xff08;机器语言&#xff09;&#xff1a;执行效率高、…
阅读更多...
【Leetcode每日一题】35.搜素插入位置|二分查找数组下标

【Leetcode每日一题】35.搜素插入位置|二分查找数组下标

&#x1f331;博主简介&#xff1a;大一计科生&#xff0c;努力学习Java中!热爱写博客~预备程序媛 &#x1f4dc;所属专栏&#xff1a;LeetCode每日一题–进击大厂 ✈往期博文回顾: 【JavaSE】保姆级教程|1万字10张图学会类与对象–建议收藏 &#x1f575;️‍♂️近期目标&…
阅读更多...
【题解】2023牛客寒假算法基础集训营2

【题解】2023牛客寒假算法基础集训营2

目录A. Tokitsukaze and abn (easy)思路B. Tokitsukaze and abn (medium)思路Tokitsukaze and abn (hard)思路D. Tokitsukaze and Energy Tree思路bfsdfsE. Tokitsukaze and Energy Tree思维F. Tokitsukaze and Gold Coins (easy)思路G. Tokitsukaze and Gold Coins (hard)H. T…
阅读更多...
高效团队的gitlab flow最佳实践

高效团队的gitlab flow最佳实践

当前git是大部分开发团队的首选版本管理工具&#xff0c;一个好的流程规范可以让大家有效地合作&#xff0c;像流水线一样有条不紊地进行团队协作。 业界包含三种flow&#xff1a; Git flowGithub flowGitlab flow 下面我们先来分析&#xff0c;然后再基于gitlab flow来设计一…
阅读更多...
19、Javaweb案例-登录功能

19、Javaweb案例-登录功能

项目导入 选择travel项目的pom.xml文件&#xff0c;点击ok&#xff0c;完成项目导入。需要等待一小会&#xff0c;项目初始化完成。 启动项目 方式一&#xff1a; 方式二&#xff1a;配置maven快捷启动 技术选型 Web层 Servlet&#xff1a;前端控制器html&#xff1a;视图Fi…
阅读更多...
【c语言】数据结构-顺序表

【c语言】数据结构-顺序表

主页&#xff1a;114514的代码大冒险 qq:2188956112&#xff08;欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ &#xff09; Gitee&#xff1a;庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 文章目录 目录 文章目录 前言 一、顺序表是什么&#xff1f; 二、项目功能的逐一实现&#xff08;基本&a…
阅读更多...
Python-Flask-2023.1.22

Python-Flask-2023.1.22

1、WSGIweb server gateway interface一个框架定义的简单通用的接口Web服务器网关接口&#xff08;Python Web Server Gateway Interface&#xff0c;缩写为WSGI&#xff09;是为Python语言定义的Web服务器和Web应用程序或框架之间的一种简单而通用的接口。flask框架内有默认的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023