什么是机制设计?
微观经济学和CS /EE的交叉学科。它采用了一种工程方法来设计激励机制,以实现战略环境中不完全信息的预期目标。机制设计具有广泛的应用,特别是在资源管理方面。
文章目录
- 1 机制设计的基础
- 1.1 简介
- 1.2 机制设计与博弈及优化的关系
- 1.3 机制设计的定义
- 1.4 机制设计的基础知识
- 1.5 拍卖机制的类别
- 1.6 设计目标
- 1.7 希望的属性限制条件
- 1.8 反向拍卖
1 机制设计的基础
1.1 简介
例1:通过拍卖出售房屋
假设你要通过拍卖出售你的房子。
- 要求每个买家送来一个密封的最终出价,然后做出决定。
- 允许买家分几轮出价,在每一轮中,他们都被告知最高出价,然后被要求修改他们的出价。
问题:(机制设计旨在解决)你应该选择哪种形式的拍卖?如何设计一个拍卖,使最高价格的交易能够达成?
例2:D2D内容共享
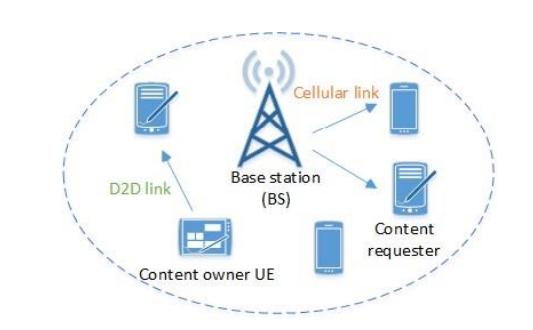
考虑一个简单的设备对设备(D2D)的内容共享模式。
- 每个UE向BS声明一个内容请求,BS决定是否为其提供服务,并选择建立蜂窝状链接或请求拥有该内容的另一个UE通过D2D链接分享该内容。
- 由于D2D消耗传输功率,如果不能得到奖励,内容所有者UE可能不愿意参与内容共享。
由于蜂窝网络有严格的容量限制,BS可以采用一种机制来鼓励D2D内容共享,以减少蜂窝流量。
- BS首先收集所有的内容请求。
- 内容所有者UE在D2D传输中竞标其成本。
- BS决定链路和功率分配,并给予奖励。
问题:(机制设计的目的是解决)如何确定最佳的资源分配和奖励?如何确保智能UE将报告其实际成本?
1.2 机制设计与博弈及优化的关系
与传统的优化问题不同。机制设计是基于个人的私人信息。机制设计关心的是个人的战略和效用。
与传统的博弈问题不同。机制设计通常有一个集中的目标。机制设计要求个人遵守规则。
机制设计与优化和博弈有一些共同的想法。因此,在解决机制设计问题时可以应用一些优化和游戏技术/算法。
1.3 机制设计的定义
机制设计的重点是设计能够产生某种预期结果的游戏。机制设计理论也被称为反向博弈理论。
机制设计的一个关键特征是,最佳分配的确定取决于代理人私下拥有的信息。
- 这种私人信息必须从代理人那里引出。
- 智能代理可能误报他们的私人信息。
- 设计一种信息交互机制, 即使代理人的行为具有战略性,结果也是最优的。
定义:机制设计可以被认为是对规则的设计,以保证完全战略代理中的理想结果。
1.4 机制设计的基础知识
拍卖是最典型的基于定价的机制之一。
一个资源分配和价格发现的过程。可以描述为:
1.问题:确定拍卖的分配和定价规则。可以允许哪些出价或如何出价?
- 应如何分配资源?
- 需要收取什么价格,或者是什么是锤子价格?
2.目标: 达到某些目标 (例如,收人最大化或者社会福利最大化)
3.基本要素:
- 买方:想购买商品的人。
- 卖家:拥有商品并愿意出售商品的人。
- 拍卖者:一个控制者(或卖方/买方本身)
- 商品:计算资源、能源、时间长度、渠道等。
- 价格:投标/要价,落锤价(最终付款)
4.术语:
- 私人信息(Private information):个人的私人偏好。
- 价值(Value):对买方需求的货币评估;价值可以是私人的。
- 竞价(Bid):基于私人信息的策略。
- 结果Outcomes(包括支付和分配,payment and allocation):根据出价决定。
- 买方的效用函数(Buyer’s utility function):价值和支付之间的差异,买方能从这次拍卖中获得的。
- 卖方的收入(Seller’s revenue):来自买方的总付款。
- 社会福利(Social welfare):所有用户(包括买家和卖家)的效用之和。
5.拍卖机制的时间线:
- 进行招标过程
- 确定最终结果
1.5 拍卖机制的类别
正向或反向:买家或卖家方面的竞争。
单边或双边:单方面或双方的竞争。
单物品或多物品:需求提供单物品或多物品的商品。
离线或在线:静态或动态(即时)。
福利或收入最大化:不同的目标。
1.6 设计目标
社会福利最大化
收入最大化
举例如下:一个拍卖机制(Q,P).
U
i
=
v
i
⋅
Q
i
(
b
i
)
−
P
i
(
b
i
,
Q
i
(
b
i
)
)
;
U
s
=
∑
i
∈
B
P
i
(
b
i
,
Q
i
(
b
i
)
)
U_i = v_i \cdot Q_i(b_i) - P_i(b_i, Q_i(b_i)) ; U_s = \sum_{i \in B} P_i(b_i, Q_i(b_i))
Ui=vi⋅Qi(bi)−Pi(bi,Qi(bi));Us=i∈B∑Pi(bi,Qi(bi))
福利最大化:
m
a
x
∑
i
∈
B
U
i
+
U
s
max \sum_{i \in B} U_i + U_s
maxi∈B∑Ui+Us
收入最大化:
m
a
x
R
s
=
U
s
=
∑
i
∈
B
P
i
(
b
i
,
Q
i
(
b
i
)
)
max R_s = U_s = \sum_{i \in B} P_i(b_i, Q_i(b_i))
maxRs=Us=i∈B∑Pi(bi,Qi(bi))
1.7 希望的属性限制条件
基本(必须包括)
- 激励相容性/真实性/战略防范性(Incentive compatibility/truthfulness/strategy-proofness,IC):没有一个买家 i 可以通过虚假出价 b i ≠ v i b_i \neq v_i bi=vi 来提高自己的效用 U i U_i Ui ,而不考虑其他买家。真实性是一种弱优势策略;纳什均衡。
- 个人合理性(Individual rationality,IR):每个真实的买方 i 在拍卖后都能获得一个非负的效用 U i U_i Ui。
- 计算效率:不是制约因素而是一种要求。
更高级的要求:
- 预算可行性
- 帕累托最优
- 抗共谋性
其他的一些分配约束(与实际应用相关)
1.8 反向拍卖
卖家方面的竞争,多个卖方竞争一个买家。
卖家的出价:反映提供商品的私人成本。例如,中继站作为卖家为源节点提供中继服务;他们的出价反映了他们在中继传输中的成本(如电力)。
目标:
- 社会成本最小化
- 支付最小化
希望的属性:
- 真实性:没有卖家可以通过虚报成本来提高其效用。
- 个人理性:每个卖家都能获得非负的效用。