Java二叉树OJ题

- 1. 检查两颗树是否相同
- 2. 另一颗树的子树
- 3. 翻转二叉树
- 4. 判断一颗二叉树是否是平衡二叉树
- - 4.1 时间复杂度为O(n*n)【从上而下递归】
  - 4.2 时间复杂度为O(n)【从下而上递归】
- 5. 对称二叉树
- 6. 二叉树的构建及遍历
- 7. 二叉树创建字符串
- 8. 两个指定节点的最近公共祖先
- - 8.1 指定结点位置分情况讨论（递归）
  - 8.2 求根到指定结点的路径（栈）
- 9. 前序与中序构造二叉树
- 10. 中序与后序构造二叉树

1. 检查两颗树是否相同

力扣100. 相同的树
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

思路：①如果p和q都为空，那么则两个结点相同（都为空，不存在有孩子）
②如果p和q中只有一个为空，那么说明两个结点不同
③如果p和q中存储的值val不相等，则说明两个结点不同
④如果值相同也不能说明两个结点相同，还要继续依照①②③对其左子树和右子树进行递归判断。

代码：

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null && q != null || p != null && q == null) {
            return false;
        }
        if (p.val != q.val) {
            return false;
        }

        return isSameTree(p.left,q.left) && isSameTree(p.right, q.right);
    }
}

2. 另一颗树的子树

力扣572. 另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

思路：结合判断两棵树是否相同，调用isSame函数。
①首先看两颗树是否是完全相同的树，传入root和subRoot，如果返回为真那么两棵树就是一模一样的树；
②排除第一种一模一样的情况，那么就递归分别判断root的左子树和右子树，一旦遇到返回值为true，就直接返回true，并且结束程序，说明是子树的关系。
代码：

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null || subRoot == null) {
            return false;
        }
        boolean flag1 = isSame(root,subRoot);
        if(flag1 == true) {
            return true;
        }
        boolean flag2 = isSubtree(root.left,subRoot);
        if(flag2 == true) {
            return true;
        }
         boolean flag3 =isSubtree(root.right,subRoot);
        if(flag3 == true) {
            return true;
        }
        return false;
    
    }
    public boolean isSame(TreeNode p, TreeNode q) {
        if(p == null && q == null) {
            return true;
        }
        if(p == null && q != null || p != null && q == null) {
            return false;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSame(p.left, q.left) && isSame(p.right, q.right);
    }
}

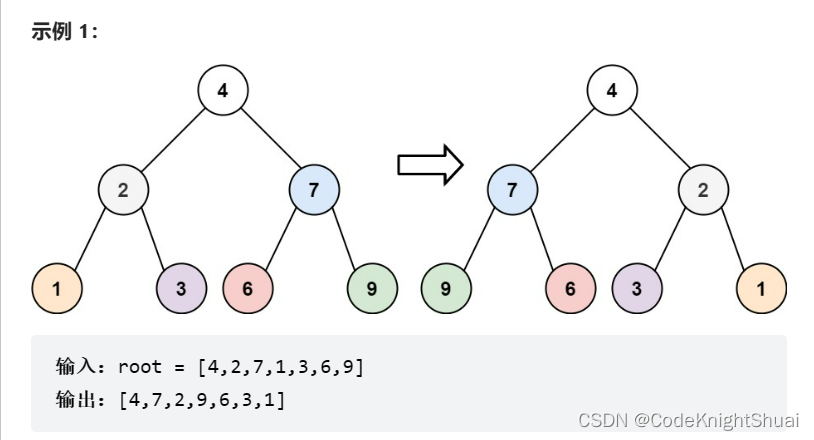
3. 翻转二叉树

力扣226. 翻转二叉树
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

思路：①如果树为空，则返回空②递归得到树的左节点，递归得到树的右结点，进行交换
代码：

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) {
            return null;
        }
        TreeNode rotl = invertTree(root.left);
        TreeNode rotr = invertTree(root.right);
        root.left = rotr;
        root.right = rotl;
        return root;
    }
}

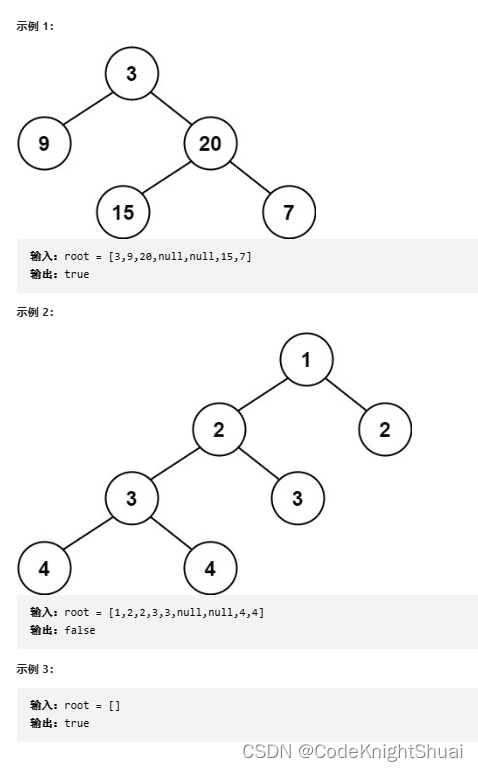
4. 判断一颗二叉树是否是平衡二叉树

力扣110. 平衡二叉树
给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

4.1 时间复杂度为O(n*n)【从上而下递归】

思路：得到每个结点的左右子树高度，利用Math库中的abs方法求差值绝对值，①绝对值小于2②左子树上的结点也满足绝对值小于2③右子树上的结点也满足绝对值小于2，则为平衡二叉树。
时间复杂度：算高度的时间复杂度是O(n)，一共有n个结点要算高度，那么时间复杂度为O(n*n)。【从上往下每个结点都算了高度，时间复杂度很高】

代码：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftHigh = getHigh(root.left);
        int rightHigh = getHigh(root.right);
        
        return Math.abs(leftHigh - rightHigh) < 2 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int getHigh(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHigh = getHigh(root.left);
        int rightHigh = getHigh(root.right);
        return leftHigh > rightHigh? leftHigh+1 : rightHigh+1;
    }
}

4.2 时间复杂度为O(n)【从下而上递归】

思路：在求高度的过程中就判断是否平衡，如果不满足平衡就返回-1。因为求根的高度的时候，实际上子树的每个结点都已经求过高度了。最后直接调用求高度的方法，传入的参数为根结点，判断是否大于等于0。

代码：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }

        return getHigh(root) >= 0;
    }

    public int getHigh(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHigh = getHigh(root.left);
        int rightHigh = getHigh(root.right);
        if (leftHigh >= 0 && rightHigh >= 0 && Math.abs(leftHigh - rightHigh) < 2) {
            return Math.max(leftHigh,rightHigh) + 1;
        }else {
            return -1;
        }
    }
}

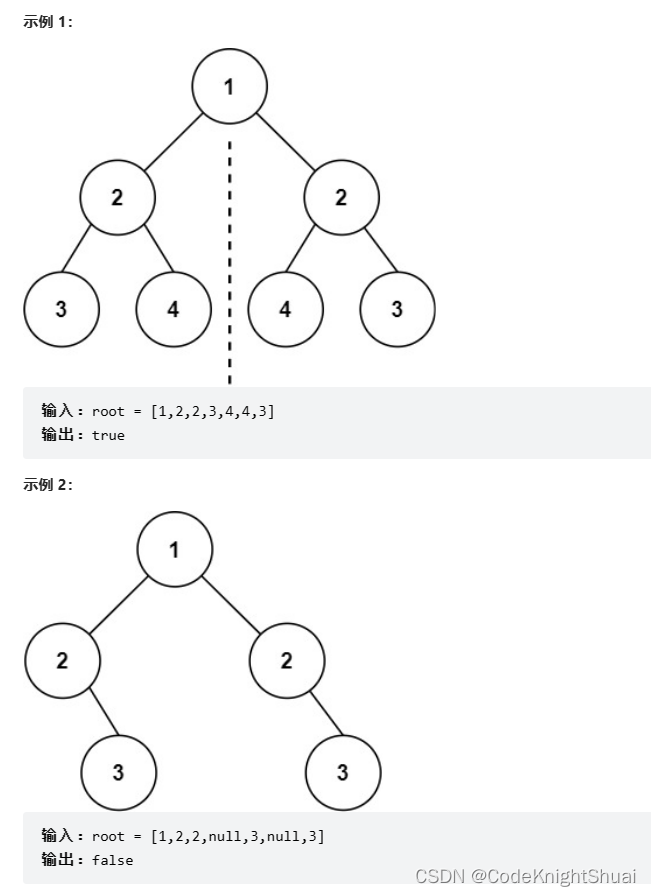
5. 对称二叉树

力扣101. 对称二叉树
给你一个二叉树的根节点 root ，检查它是否轴对称。

思路：写一个判断2个结点是否相同的方法，①如果2个结点都为空那么是相同②如果有且只有一个为空，那么2个结点不相同③如果两个结点的值不相同，则2个两点不相同；依次递归判断结点A的左子树与结点B的右子树，结点A的右子树与结点B的左子树。
代码：

    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return isSym(root.left,root.right);
    }

    public boolean isSym(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null && q != null || p != null && q == null) {
            return false;
        }
        if (p.val != q.val) {
            return false;
        }
        return isSym(p.left,q.right) && isSym(p.right,q.left);
    }

6. 二叉树的构建及遍历

牛客KY11 二叉树遍历
编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。
示例1
输入：
abc##de#g##f###
输出：
c b e g d f a

思路：
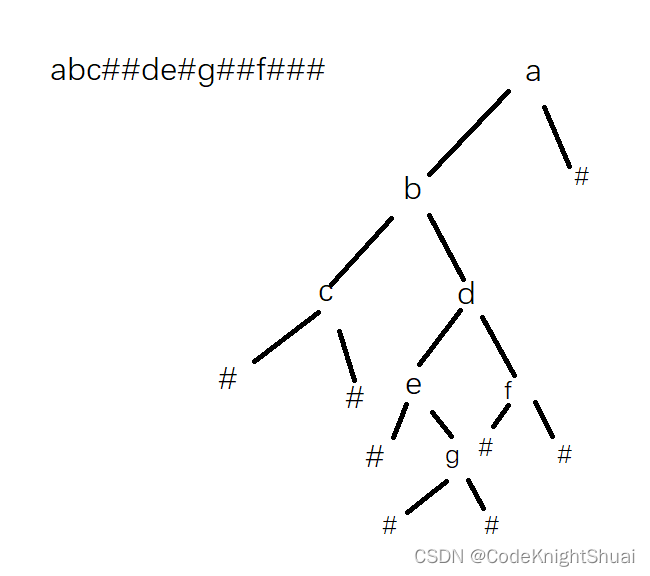
在这里插入图片描述
接受输入的字符串，一个一个遍历字符串中的字符，如果字符不是#，那么就递归建立左子树，如果遇见#那就跳过这个字符，进行下一次的递归，左走完了就走右。
代码：

import java.util.Scanner;

class BinaryTreeNode {
    char val;
    BinaryTreeNode left;
    BinaryTreeNode right;

    public BinaryTreeNode(char val) {
        this.val = val;
    }
}

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextLine()) {
            String s = scanner.nextLine();
            BinaryTreeNode root = createNode(s);
            inOrder(root);
        }
    }
    public static int i = 0;
    private static BinaryTreeNode createNode(String s) {
        BinaryTreeNode root = null;
        if (s.charAt(i) != '#') {
            root = new BinaryTreeNode(s.charAt(i));
            i++;
            root.left = createNode(s);
            root.right = createNode(s);
        }else {
            i++;
        }
        return root;
    }
    public static void inOrder(BinaryTreeNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }
}

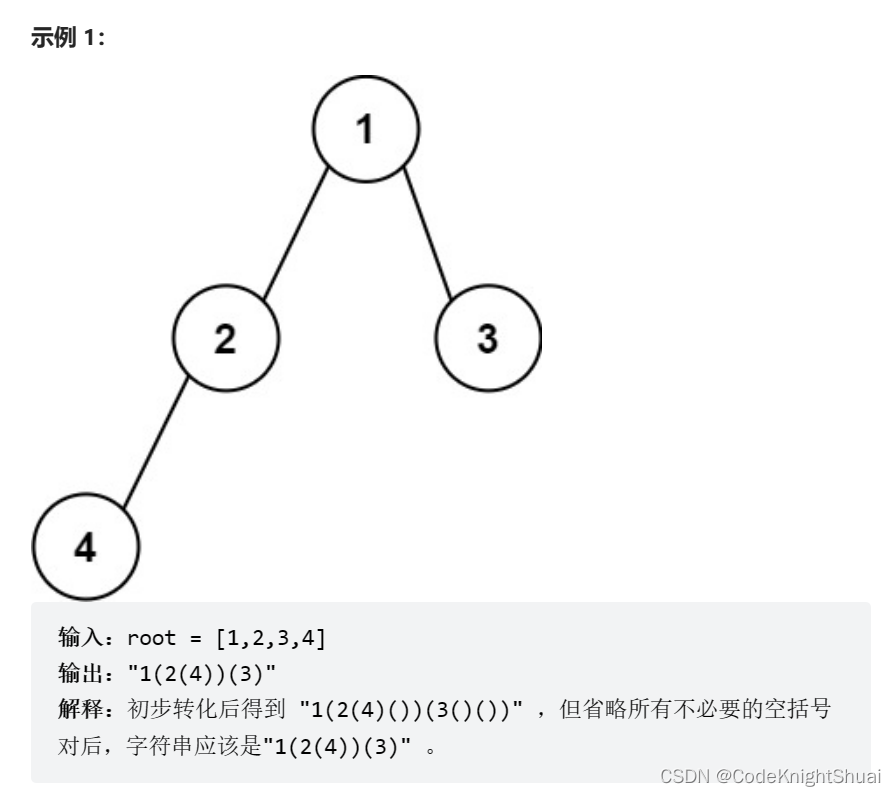
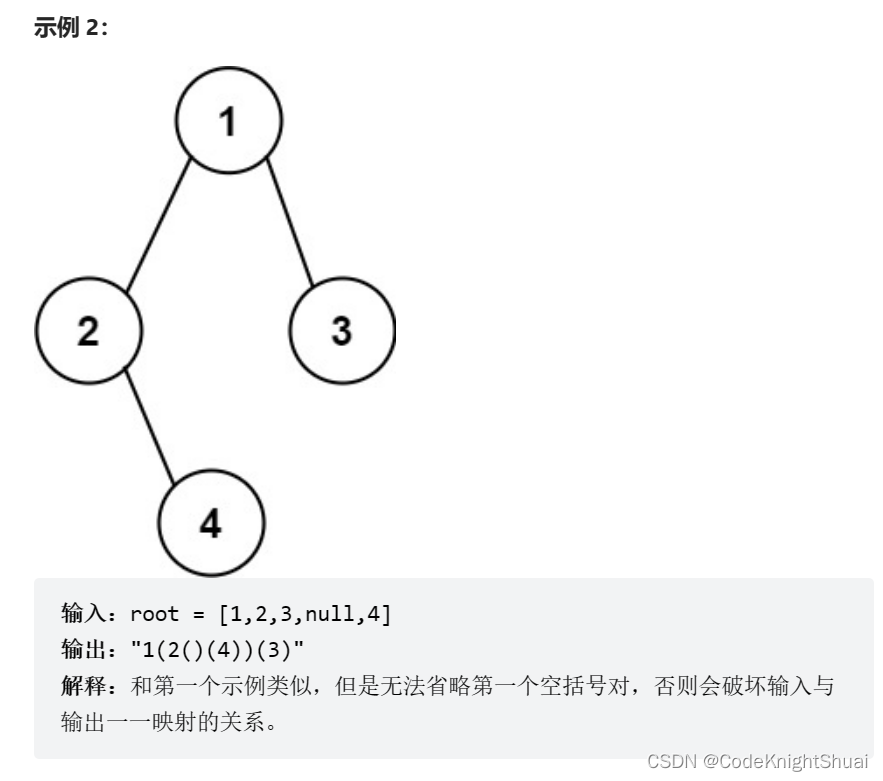
7. 二叉树创建字符串

力扣606. 根据二叉树创建字符串
给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。
空节点使用一对空括号对 “()” 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

思路：实例化一个StringBuilder对象，并实现treeStr完成二叉树转字符串的方法。
①如果二叉树的左节点不为空，则需要“（” + 递归左结点 + “）”
②如果二叉树的左节点为空，Ⅰ：右结点也为空，则直接返回；Ⅱ：右节点不为空，则需要给左节点为空的那个位置加上括号“（” “）”，执行下面的另起分支的右节点的情况
③如果二叉树的右结点为空，则什么都不操作
④如果二叉树的右节点不为空，则需要“（” + 递归右结点 + “）”

代码：

    public String tree2str(TreeNode root) {
        StringBuilder stringBuilder = new StringBuilder();
        treeStr(root,stringBuilder);
        return stringBuilder.toString();
    }
    public void treeStr(TreeNode root, StringBuilder stringBuilder) {
        if (root == null) {
            return;
        }
        stringBuilder.append(root.val);
        if (root.left != null) {
            stringBuilder.append("(");
            treeStr(root.left,stringBuilder);
            stringBuilder.append(")");
        }else {
            if (root.right == null) {
                return;
            }else {
                stringBuilder.append("()");
            }
        }
        if (root.right == null) {
            return;
        }else {
            stringBuilder.append("(");
            treeStr(root.right,stringBuilder);
            stringBuilder.append(")");
        }
    }

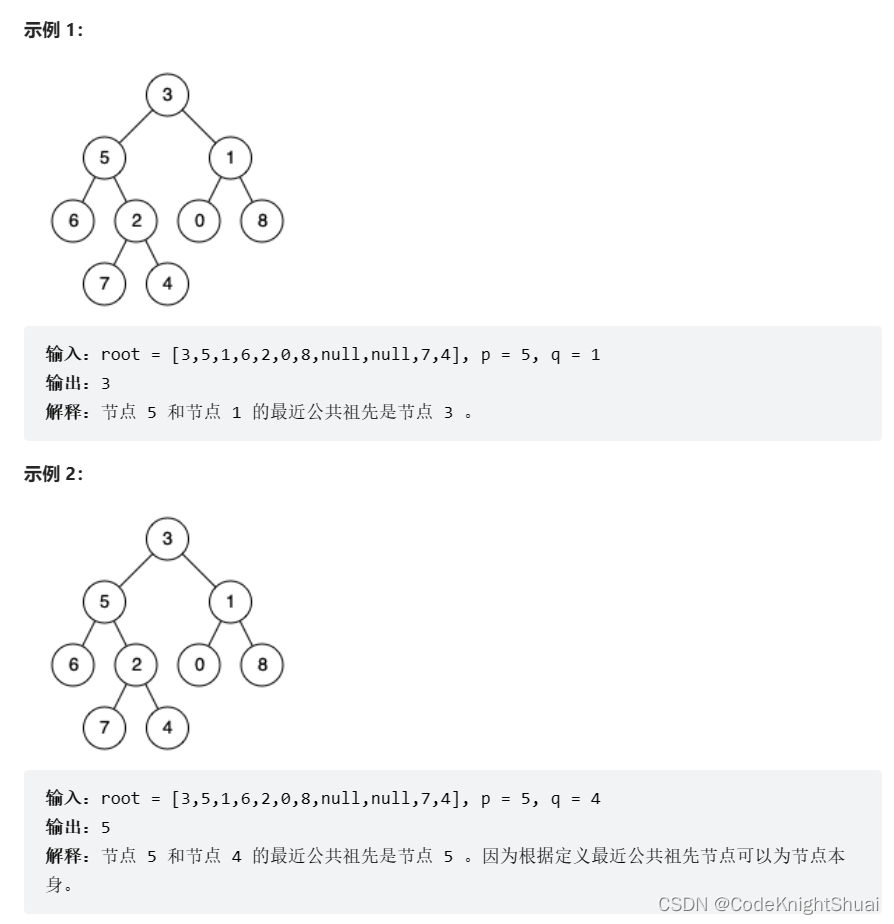
8. 两个指定节点的最近公共祖先

力扣236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

8.1 指定结点位置分情况讨论（递归）

思路：存在以下3种情况
在这里插入图片描述

代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == p || root == q) {
            return root;
        }
        if(root == null) {
            return null;
        }
        TreeNode leftNode = lowestCommonAncestor(root.left,p,q);
        TreeNode rightNode = lowestCommonAncestor(root.right,p,q);
        if(leftNode != null && rightNode != null) {
            return root;
        }else if(leftNode != null) {
            return leftNode;
        }else if(rightNode != null) {
            return rightNode;
        }
        return null;
    }
}

8.2 求根到指定结点的路径（栈）

【难点：如何把根结点到指定结点路上的所有结点找到放到栈里面】
思路：把根结点到指定结点的路径存到栈中，其方法的具体实现是如果递归找到了目标结点就返回真，如果走错路径了就弹出栈重新递归。最后得到2个栈，让栈元素多的那个不断出栈直至2个栈元素个数相等，再依次弹出判断是否有结点相同。
代码：

class Solution {
    private boolean getPath(TreeNode root, TreeNode g, Stack<TreeNode> stack) {
        if (root == null || g == null) {
            return false;
        }
        stack.push(root);
        if (root == g) {
            return true;
        }
        boolean leftFlag = getPath(root.left,g,stack);
        if (leftFlag == true) {
            return true;
        }
        boolean rightFlag = getPath(root.right,g,stack);
        if (rightFlag == true) {
            return true;
        }
        stack.pop();
        return false;
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //分别获取root到p和root到q的路径存储到栈中
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();
        getPath(root,p,stack1);
        getPath(root,q,stack2);
        int size1 = stack1.size();
        int size2 = stack2.size();
        if (size1 > size2) {
            int size = size1 - size2;
            while (size > 0) {
                stack1.pop();
                size--;
            }
        }else {
            int size = size2 - size1;
            while (size > 0) {
                stack2.pop();
                size--;
            }
        }
        //相等了
        while (!stack1.isEmpty()) {
            TreeNode t1 = stack1.pop();
            TreeNode t2 = stack2.pop();

            if (t1.val == t2.val) {
                return t1;
            }
        }
        return null;
    }
}

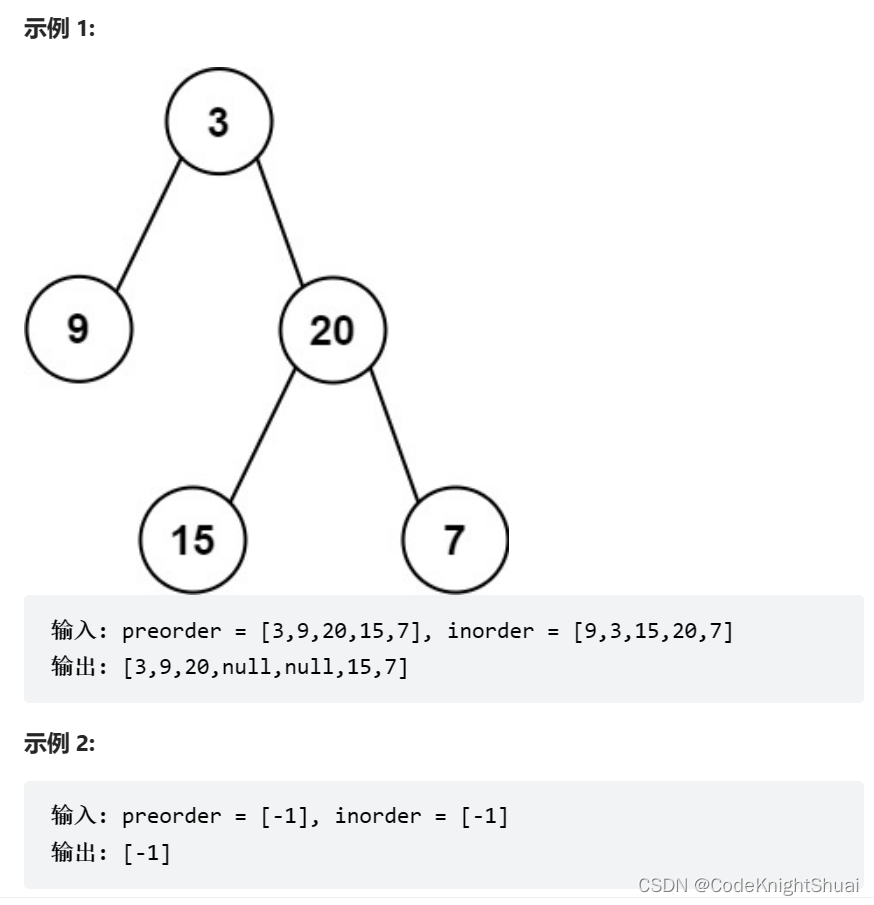
9. 前序与中序构造二叉树

力扣105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思路：前序遍历得到根，中序遍历可以区分根的左子树和右子树，再在前序遍历中得到左子树的根，以此类推递归下去。

代码：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        TreeNode ret = createTree(preorder,inorder,0,inorder.length-1);
        return ret;
    }
    public int i = 0;
    public TreeNode createTree(int[] preorder, int[] inorder, int ib, int ie) {
        if (ib > ie) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[i]);
        int index = findRoot(inorder,preorder[i]);
        i++;
        root.left = createTree(preorder,inorder,ib,index - 1);
        root.right =createTree(preorder,inorder,index+1,ie);
        return root;
    }
    private int findRoot(int[] inorder, int x) {
        for (int j = 0; j < inorder.length; j++) {
            if (inorder[j] == x) {
                return j;
            }
        }
        return -1;
    }
}

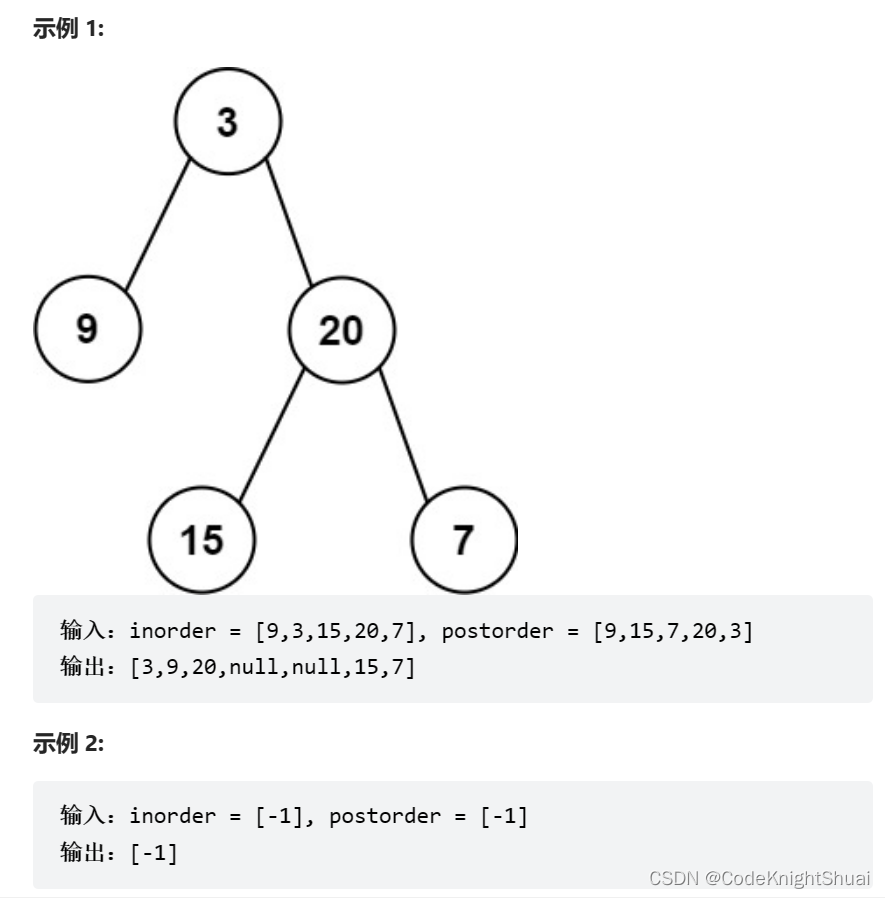
10. 中序与后序构造二叉树

力扣106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

思路：后序遍历的最后一个结点是根，中序遍历可以区分根的左子树和右子树，依次类推，但是要注意后序遍历序列根的前面是右子树的根，因此要先创建右子树。

代码：

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        i = postorder.length - 1;
        return createTree(inorder,postorder,0,inorder.length-1);
    }
    public int i = 0;
    private TreeNode createTree(int[] inorder, int[] postorder, int ib, int ie) {
        if (ib > ie) {
            return null;
        }
        TreeNode root = new TreeNode(postorder[i]);
        int index = findRoot(inorder,postorder[i]);
        i--;
        root.right = createTree(inorder,postorder,index+1,ie);
        root.left = createTree(inorder,postorder,ib,index - 1);
        return root;
    }
        private int findRoot(int[] inorder, int x) {
        for (int j = 0; j < inorder.length; j++) {
            if (inorder[j] == x) {
                return j;
            }
        }
        return -1;
    }
}