写在前面:矩阵连乘的要点
1、最优解数组的含义--A[1:n]的最少数乘次数
2、数组的填写方向--斜着填
3、递推方程含义
今天开始动态规划的学习,动态规划与分治法类似,基本思想就是将待求解的问题分成若干子问题,先求解子问题,再结合这些子问题,得到源问题的解。
与分治法不同的是,动态规划求解的问题往往不是相互独立的,分治法来求解这些问题,子问题数目会很多,有些子问题会被重复计算很多次,如果能够保存已经解决的问题的答案,就可以避免大量重复计算。
动态规划适用于求解最优化问题,通常有4个步骤
1、找出最优解的性质,刻画其结构特征
2、递归的定义最优值
3、以自底向下的方式计算最优值
4、根据计算最优值时得到的信息,构造最优解
问题描述
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
乘法次数可以理解为:A矩阵的规模为p × q ,B矩阵的规模为q × r,C=AB,则C矩阵的规模为p×r,每个位置上的元素需要q次乘法然后相加得到,一共需要p×q×r次数乘。例如,给定三个连乘矩阵{A1,A2,A3}的维数分别是10*100,100*5和5*50,采用(A1A2)A3,乘法次数为10*100*5+10*5*50=7500次,而采用A1(A2A3),乘法次数为100*5*50+10*100*50=75000次乘法,显然,最好的次序是(A1A2)A3,乘法次数为7500次。
分析:
矩阵链乘法问题描述:
给定由n个矩阵构成的序列{A1,A2,...,An},对乘积A1A2...An,找到最小化乘法次数的加括号方法。简记为:A[1:n]
1)寻找最优子结构
此问题最难的地方在于找到最优子结构。对乘积A1A2...An的任意加括号方法都会将序列在某个地方分成两部分,也就是最后一次乘法计算的地方,我们将这个位置记为k,也就是说首先计算A1...Ak和Ak+1...An,然后再将这两部分的结果相乘。简记为:A[1:k] 和A[k+1,n]
最优子结构如下:假设A1A2...An的一个最优加括号把乘积在Ak和Ak+1间分开,则前缀子链A[1:k]的加括号方式必定为A1...Ak的一个最优加括号,如果计算A[1:k]的次序需要更少的计算量,那么更新最优值之后,得到的A[1:n]的计算量也将是最优的,后缀子链同理。
一开始并不知道k的确切位置,需要遍历所有位置以保证找到合适的k来分割乘积。
2)构造递归解
设m[i,j]为矩阵链Ai...Aj的最优解的代价,则

当i=j时,A[i:j]=Ai是单一矩阵无需计算,因此,m[i,i]=0,i=1,2,…,n
当i<j时,计算的A[ i : j ]在k处断开,则![]()
这里的 k 有 j-i 种可能。需要用一个新的循环来遍历k的值,k是这 j-i 个位置中使得乘法计算量最小的那个位置。把所有k的位置保存起来,记为S[i][j],在计算出最后的M[i][j]后,可以递归的还原k然后构造最优解。
3)构建辅助表,解决重叠子问题
对于一组矩阵:A1(30x35),A2(35x15),A3(15x5),A4(5x10),A5(10x20),A6(20x25) 个数N为6
那么p数组保存它们的行数和列数:p={30,35,15,5,10,20,25}共有N+1即7个元素
p[0],p[1]代表第一个矩阵的行数和列数,p[1],p[2]代表第二个矩阵的行数和列数......p[5],p[6]代表第六个矩阵的行数和列数

辅助表m: m[i][j]代表从矩阵Ai,Ai+1,Ai+2......直到矩阵Aj最小的相乘次数,比如A[2][5]代表A2A3A4A5最小的相乘次数,即最优的乘积代价。从矩阵A2到A5有三种断链方式:A2{A3A4A5}、{A2A3}{A4A5}、{A2A3A4}A5,这三种断链方式会影响最终矩阵相乘的计算次数,我们分别算出来,然后选一个最小的,就是m[2][5]的值,同时保留断开的位置k在s数组中。
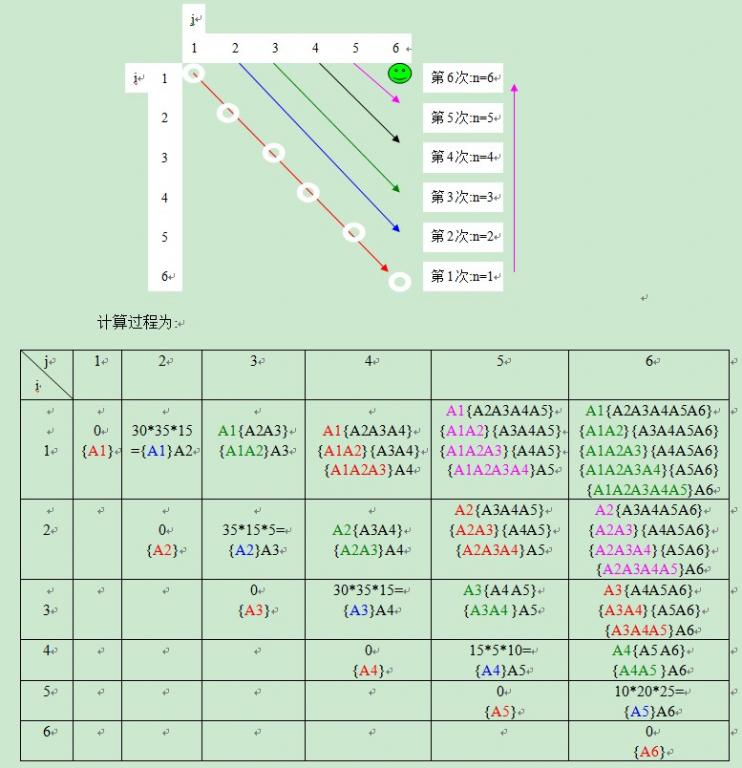
斜着填表,for循环的控制要写对!
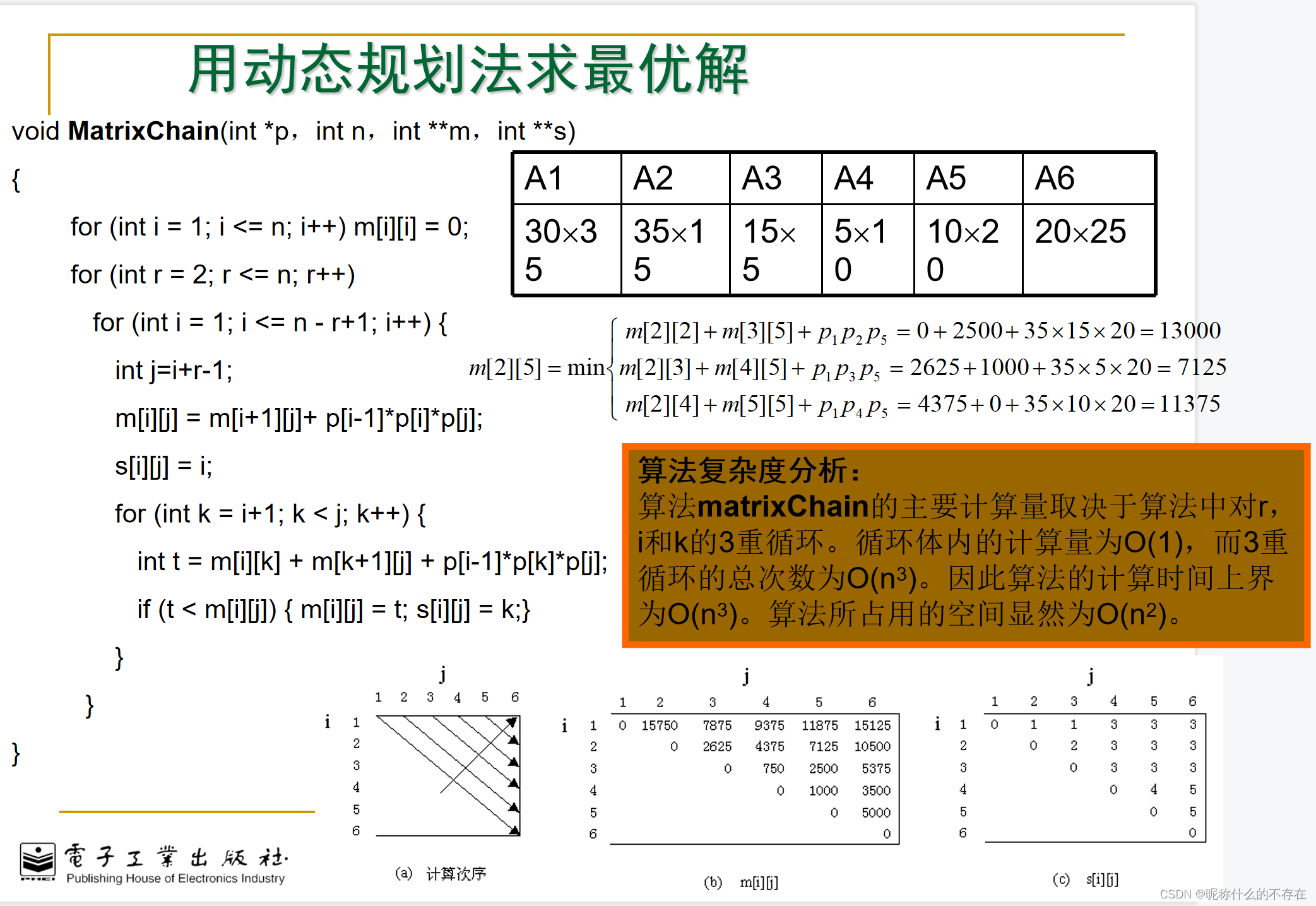
r表示问题规模,从2开始,因为1是单个矩阵不需要计算直接都填0
i表示行号,一行一行遍历,j表示列号,斜着填写,根据问题规模来,行号+问题规模-1(下标问题),m[i][j]是递推方程,k需要遍历j-i次,才能找到最优的那个位置。
#include<iostream>
using namespace std;
const int N=7;
//p为矩阵链,p[0],p[1]代表第一个矩阵的行数和列数,p[1],p[2]代表第二个矩阵的行数和列数......length为p的长度
//所以如果有六个矩阵,length=7,m为存储最优结果的二维矩阵,s为存储选择最优结果路线的
//二维矩阵
void MatrixChainOrder(int *p,int m[N][N],int s[N][N],int length)
{
int n=length-1;
int l,i,j,k,q=0;
//m[i][i]只有一个矩阵,所以相乘次数为0,即m[i][i]=0;
for(i=1;i<length;i++)
{
m[i][i]=0;
}
//l表示矩阵链的长度
// l=2时,计算 m[i,i+1],i=1,2,...,n-1 (长度l=2的链的最小代价)
for(l=2;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1; //以i为起始位置,j为长度为l的链的末位,
m[i][j]=0x7fffffff;
//k从i到j-1,以k为位置划分
for(k=i;k<=j-1;k++)
{
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
}
}
}
cout << m[1][N-1] << endl;
}
void PrintAnswer(int s[N][N],int i,int j)
{
if(i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PrintAnswer(s,i,s[i][j]);
PrintAnswer(s,s[i][j]+1,j);
cout<<")";
}
}
int main()
{
int p[N]={30,35,15,5,10,20,25};
int m[N][N],s[N][N];
MatrixChainOrder(p,m,s,N);
PrintAnswer(s,1,N-1);
return 0;
}•利用问题的最优子结构性质,以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。