《啊哈算法第四章之bfs》（17张图解）

news2024/9/25 1:20:24

源自《啊哈算法》 

目录

bfs正文

题目

思路 

完整代码1

完整代码2 

再解炸弹人

题目

思路

完整代码1

完整代码2

总结

bfs正文

第四章--深度优先搜索中，我们用dfs找到了寻找小哈的最短路径

接下来，我们要用bfs（Breadth First Search）找到最短路径，并输出最少的步数

 

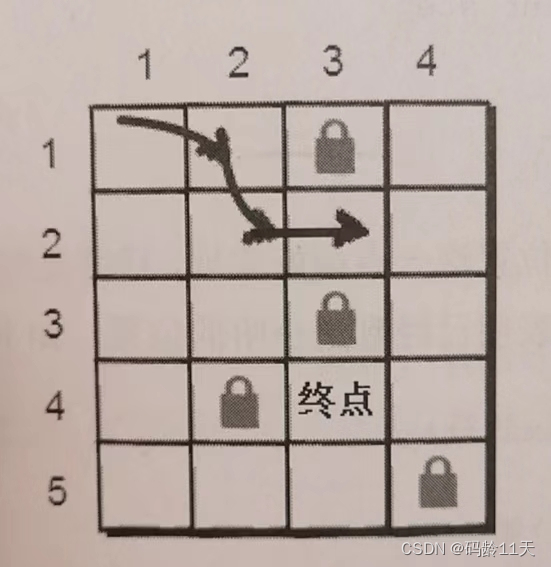
题目

1，有一天，我的女朋友一个人去玩迷宫，因为方向感很差，迷路了，我得知后马上去解救她

2，迷宫由m行n列的单元格组成（m和n都小于100），每个单元格要么是空地，要么是障碍

3，我的任务是帮助女朋友找到一条从迷宫起点通向女朋友位置的最短路径

4，注意障碍是不能走的，也不能走到迷宫外

思路 

本题中，bfs通过寻找一步以内（相对起点）可以到达的点，两步以内可以到达的点，三步以内....直到找到终点（目标点），或是把所有点都加入队列里

 最开始小哼在（1，1）处，上一节dfs中我们的方法是，先让小哼往任意一个可行方向走，然后一直尝试下去，直到走不通就返回这里，这时深度优先，通过递归实现

本节我们通过“一层一层”扩展的方法找到小哈，扩展时每发现一个点，就将这个点加入到队列中，直至走到小哈的位置（p, q）为止 

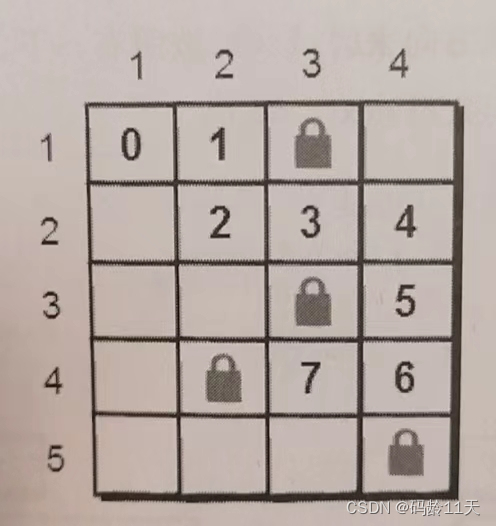
最开始小哼在入口（1，1）处，一步之内（距离入口）可以到达的点有（1，2）和（2，1）

但小哈不在这两个点上，小哼只能通过（1，2）和（2，1）这两点继续往下走

当小哼走到（1，2），两步之内可以到达的点有（2，2）；

当小哼走到（2，1）， 两步之内可以到达的点有（2，2）和（3，1）

这时我们发现（2，2）这个点可以通过（1，2）到达，也可以通过（2，1）到达，此时需要一个数组标记某个点是否被访问过 

当然我们可以不需要，可以通过存储迷宫的二维数组直接操作，具体优化代码后面会有

同理，我们找到三步之内可以到达的点有（2，3），（3，2），（4，1）

但是依然没有到达小哈所在点，我们需要重复上述步骤，直到发现小哈

回顾刚才的算法，我们用结构体实现队列来模拟这个过程 

struct note
{
    int x; //横坐标
    int y; //纵坐标
    int s; //步数
};
struct note que[2501]; //地图大小不超过50*50，队列扩展在2500个以内
int head, tail;
int a[51][51] = {0}; //存储迷宫地图
int book[51][51] = {0}; //标记走过的点，防止被重复扩展

//初始化队列
head = 1;
tail = 1;
//先将（1，1）加入队列，并标记
que[tail].x = 1;
que[tail].y = 1;
que[tail].s = 0;
tail++;
book[1][1] = 1;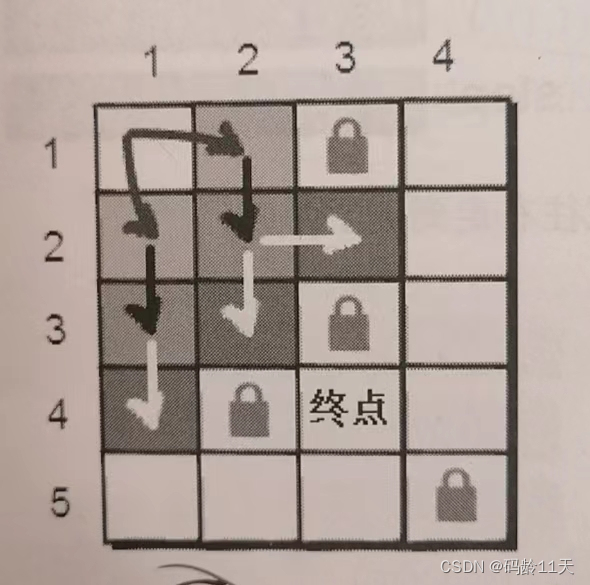

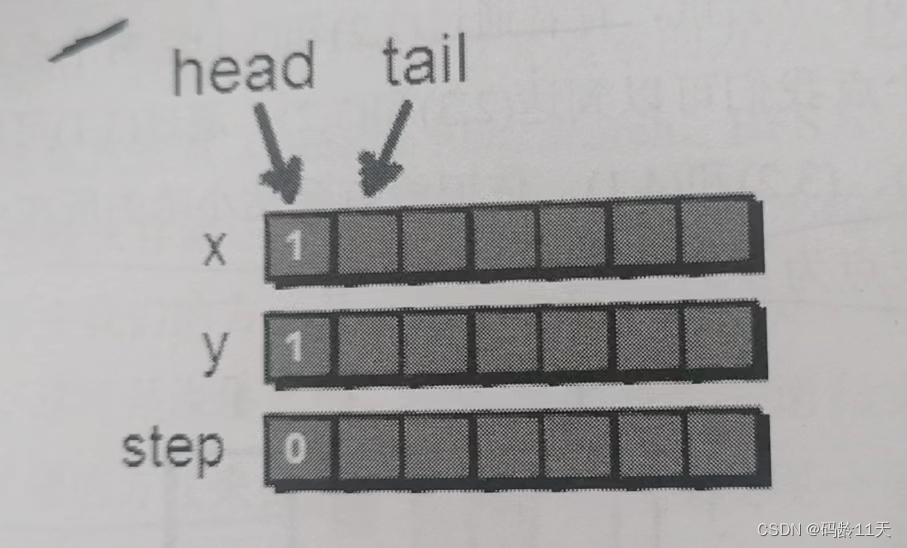
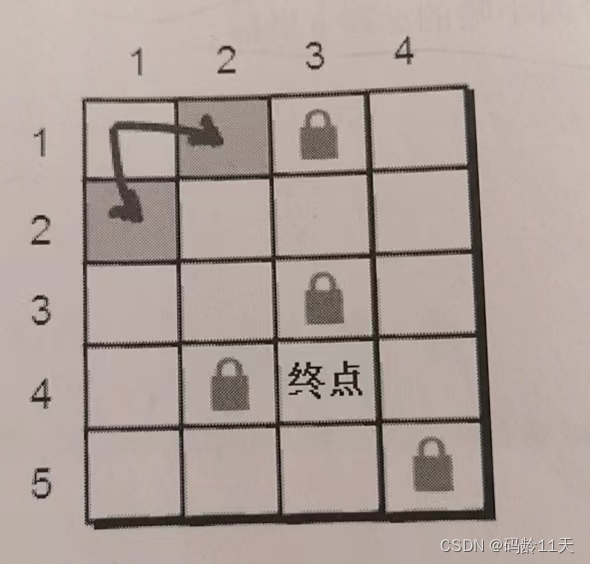
然后从(1,1)开始,先尝试往右走到达了(1,2)

tx = que[head].x;
ty = que[head].y + 1; //tx, ty为临时变量

需要判断(1,2)是否越界

if(tx < 1 || ty < 1 || tx > m || ty > m)
    continue;

再判断(1,2)是否为障碍或是否走过

if(a[tx][ty] == 0 && book[tx][ty] == 0)

 如果满足上面的条件,将(1,2)入队,并标记该点已经走过

book[tx][ty] = 1;
//注意bfs每个点只入队一次,不需要将book数组取消标记

//插入新的点到队列中
que[tail].x = tx;
que[tail].y = ty;
que[tail].s = que[head].s + 1; //步数是父亲步数 + 1
tail++;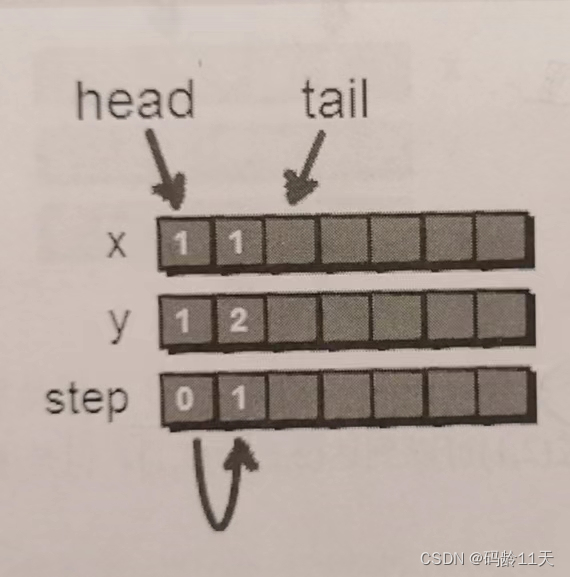

 

 接下来尝试往其他方向走,从(1,1)也可以到达(2,1),所以将(2,1)也加入队列,代码实现与上述一样

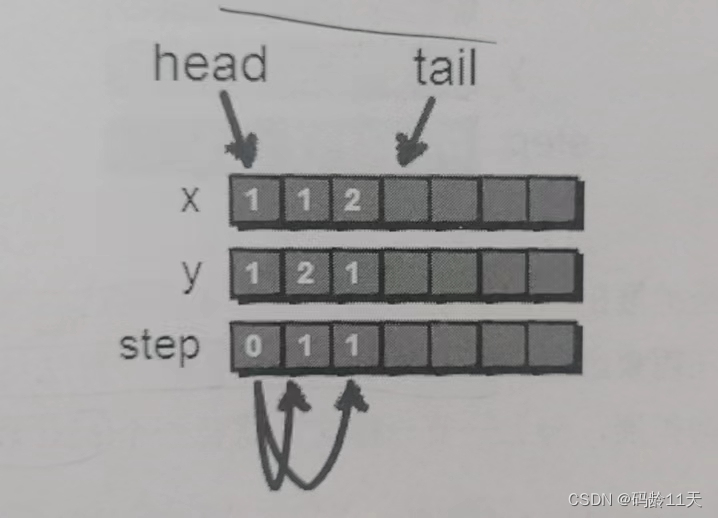
 对(1,1)扩展完后,(1,1)就没用了,此时将(1,1)出队,出队操作如下

head++;

 接下来在新扩展出的(1,2)和(2,1)上往下探索,目前为止已扩展出从起点出发,一步以内可以到达的所有点,因为未到达女朋友的位置,所以继续

(1,1)出队后,队列中head指向(1,2),我们需要通过(1,2)继续扩展,通过(1,2)可到达(2,2),将(2,2)也加入队列 

(1,2)扩展完毕,也没用了,就将(1,2)出队. (1,2)出队后,head指向(2,1)这个点. 通过(2,1)可以到达(2,2)和(3,1),但因为(2,2)已经在队列中,因此只将(3,1)入队

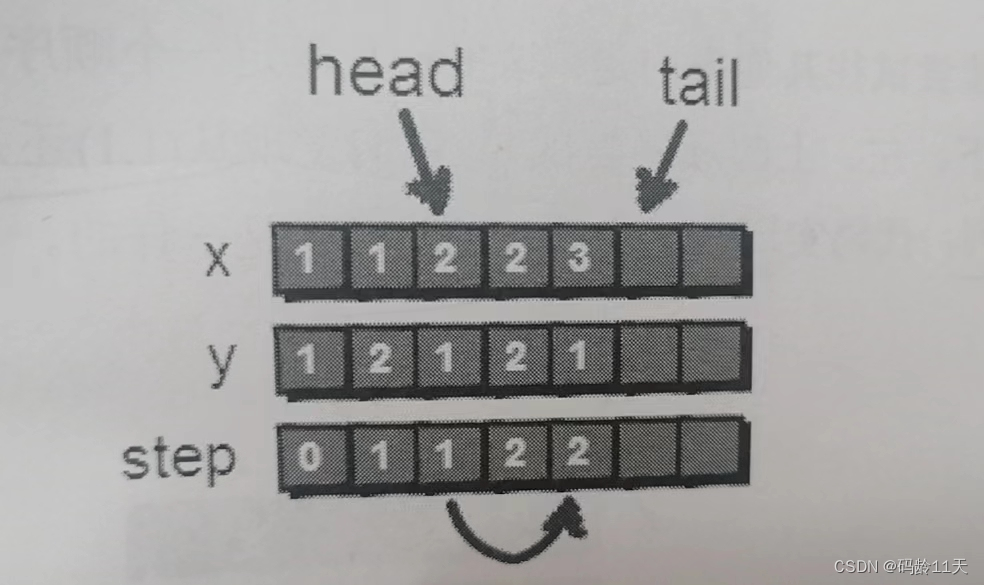
截至目前,我们已经扩展出从起点出发两步以内可以到达的所有点,可依旧没到达女朋友的位置,因此继续重复上述步骤,知道遇到小哈,算法结束.

为了方便向四个方向扩展,我们需要一个next数组 

int next[4][2] = {{-1, 0},//上
                  {1, 0}, //下
                  {0, -1},//左
                  {0, 1}};//右

完整代码1

#include<cstdio> //scanf(), printf()
struct note
{
    int x; //横坐标
    int y; //纵坐标
    int f; //父坐标，本题不要求输出路径，不需要
    int s; //步数
};
int main()
{
    struct note que[2501]; //50*50地图，队列扩展不超2500

    int a[51][51] = {0}, book[51][51] = {0};
    int next[4][2] = {{-1, 0}, //上
                      {1, 0},  //下
                      {0, -1}, //左
                      {0, 1}}; //右
    int head, tail;
    int i, j, k, n, m, startx, starty, p, q, tx, ty, flag;

    scanf("%d %d", &n, &m);
    for(i = 1; i <= n; ++i)
        for(j = 1; j <= m; ++j)
            scanf("%d", &a[i][j]);
    scanf("%d %d %d %d", &startx, &starty, &p, &q);

    //队列初始化
    head = 1;
    tail = 1;
    //往队列插入迷宫入口坐标
    que[tail].x = startx;
    que[tail].y = starty;
    que[tail].s = 0;
    que[tail].f = 0;
    tail++;
    book[startx][starty] = 1;

    flag = 0; //标记是否到达目标点，1表示已到达
    //当队列不为空时
    while(head < tail) {
        //枚举四个方向
        for(k = 0; k <= 3; ++k) {
            tx = que[head].x + next[k][0];
            ty = que[head].y + next[k][1];
            //判断越界
            if(tx < 1 || ty < 1 || tx > n || ty > m)
                continue;
            //判断不为障碍且未走过
            if(a[tx][ty] == 0 && book[tx][ty] == 0) {
                //bfs每个点只入队一次
                book[tx][ty] = 1;
                //插入新的点到队列中
                que[tail].x = tx;
                que[tail].y = ty;
                que[tail].f = head; //本题不用
                que[tail].s = que[head].s + 1; //上一步的基础上+1
                tail++; //放最后
            }
            //若达目标点，停止扩展，退出循环
            if(tx == p && ty == q) {
                flag = 1;
                break;
            }
        }
        if(flag) break;
        head++; //继续后续点的扩展
    }
    //tail指向队尾的下一位，所以减1
    printf("%d", que[tail - 1].s);
    return 0;
}

5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
7

下面是关于去掉book数组的优化,只需在原迷宫数组基础上,把去过的点赋值为-1就好

完整代码2 

#include<cstdio> //scanf(), printf()
struct note
{
    int x; //横坐标
    int y; //纵坐标
    int f; //父坐标，本题不要求输出路径，不需要
    int s; //步数
};
int main()
{
    struct note que[2501]; //50*50地图，队列扩展不超2500

    int a[51][51] = {0};
    int next[4][2] = {{-1, 0}, //上
                      {1, 0},  //下
                      {0, -1}, //左
                      {0, 1}}; //右
    int head, tail;
    int i, j, k, n, m, startx, starty, p, q, tx, ty, flag;

    scanf("%d %d", &n, &m);
    for(i = 1; i <= n; ++i)
        for(j = 1; j <= m; ++j)
            scanf("%d", &a[i][j]);
    scanf("%d %d %d %d", &startx, &starty, &p, &q);

    //队列初始化
    head = 1;
    tail = 1;
    //往队列插入迷宫入口坐标
    que[tail].x = startx;
    que[tail].y = starty;
    que[tail].s = 0;
    que[tail].f = 0;
    tail++;
    a[startx][starty] = -1;

    flag = 0; //标记是否到达目标点，1表示已到达
    //当队列不为空时
    while(head < tail) {
        //枚举四个方向
        for(k = 0; k <= 3; ++k) {
            tx = que[head].x + next[k][0];
            ty = que[head].y + next[k][1];
            //判断越界
            if(tx < 1 || ty < 1 || tx > n || ty > m)
                continue;
            //判断不为障碍且未走过
            if(a[tx][ty] == 0) {
                //bfs每个点只入队一次
                a[tx][ty] = -1;
                //插入新的点到队列中
                que[tail].x = tx;
                que[tail].y = ty;
                que[tail].f = head; //本题不用
                que[tail].s = que[head].s + 1; //上一步的基础上+1
                tail++; //放最后
            }
            //若达目标点，停止扩展，退出循环
            if(tx == p && ty == q) {
                flag = 1;
                break;
            }
        }
        if(flag) break;
        head++; //继续后续点的扩展
    }
    //tail指向队尾的下一位，所以减1
    printf("%d", que[tail - 1].s);
    return 0;
}

输出是一样的,只是把book数组删去,在对应位置上补上a[tx][ty] = 1即可 

再解炸弹人

分别用bfs和dfs解决问题

题目

 还记得小霸王游戏机上的“炸弹人”吗，用放置炸弹的方法来消灭敌人

炸弹的爆炸方向沿上下左右四个方向

问在哪里放置炸弹可以消灭最多的敌人，已知两种墙，一种可以被炸掉

由于现在只有一枚炸弹，所以墙都用"#"表示（一枚炸弹可以炸掉这种墙，但也会被挡住）

敌人用"G"表示，空地用"."表示，只有空地才能放置炸弹

要求：统计炸弹放在哪个空地上，消灭的敌人最多（上下左右四个方向敌人个数的和）

输出消灭敌人最多的坐标，以及消灭的人数

思路

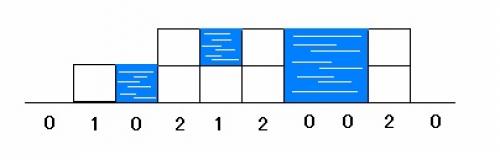
按照枚举的办法，炸弹放在（1，11）处，最多可消灭11个敌人，注意是从（0，0）开始计算，但小人无法走到（1，11），所以正确答案是放在（7，11）处，可消灭10个敌人

我们使用bfs或dfs（搜索）来枚举出所有小人可以到达的点，然后在这些点分别统计消灭的人数

 

（ 先用bfs）

1，起点

小人从点（3，3）开始扩展，先将（3，3）入队，计算出该点可消灭的敌人数量

2，一步以内

通过（3，3）扩展出（2，3），（4，3），（3，2），（3，4），并将这些点入队，再分别计算每个点消灭人数

3，两步以内......

接下来，再通过（2，3）开始扩展......

4，直至所有点扩展完毕，bfs结束，最后输出扩展出的点里，消灭敌人最多的坐标和敌人数量

采用结构体实现队列，需要x, y记录坐标 

struct note
{
    int x, y; //横，纵坐标
};
struct note que[401]; //地图最大20*20，队列扩展最多400
int head, tail;
char a[20][20]; //存储地图

 初始化队列，设置为空（head == tail）

head = 1;
tail = 1;

 队列中插入起始坐标(startx, starty)，并标记已在队列中 

que[tail].x = startx;
que[tail].y = starty;
tail++;
a[startx][starty] = -1; //标记已在队列中

 统计炸弹在该点消灭的敌人数量，方法与《啊哈算法》第三章一样《啊哈算法》第三章--枚举很暴力_码龄11天的博客-CSDN博客

此处将某点（i，j）放置炸弹消灭的人数，写成一个函数，函数名为getnum，方便后续调用

sum = getnum(i, j);

 还需要一个next数组便于往四个方向扩展

int next[4][2] = {{-1, 0}, //上
                  {1, 0},  //下
                  {0, -1}, //左
                  {0, 1}}; //右

 接下来开始扩展，也是bfs的核心部分

while(head < tail) {
    //枚举四个方向
    for(k = 0; k < 4; ++k) {
        tx = que[head].x + next[k][0];
        ty = que[head].y + next[k][1];

        //判断越界
        if(tx < 0 || ty < 0 || tx > n - 1 || ty > m - 1)
            continue; //换另一个方向
    
        //未走过的空地
        if(a[tx][ty] == '.') {
            //每个点只入队一次
            a[tx][ty] = -1;
            //插入新扩展的点到队列中
            que[tail].x = tx;
            que[tail].y = ty;
            tail++;
            
            //统计新扩展的点，消灭敌人人数
            sum = getnum(tx, ty);
            //更新max值
            if(sum > max) {
                max = sum;
                mx = tx;
                my = ty;
            }
        }
    }
    head++; //一个点扩展结束后，head++才能对后续点扩展
}

以上就是bfs基本实现过程 

如果换dfs的话，从起点开始，每走到一个新点就统计该点消灭的人数，并从该点继续往后尝试，直到无路可走返回，再尝试其他没走过的方向，直到所有点都访问一遍

void dfs(int x, int y)
{
    int k, sum, tx, ty;
    //计算人数
    sum = getnum(x, y);
    //更新值和坐标
    if(sum > Max)
    { Max = sum; mx = x; my = y; }
    //方向数组
    int next[4][2] = {{-1, 0},{1, 0},{0, -1},{0, 1}};
    //枚举四个方向
    for(k = 0; k < 4; ++k) {
        //下一节点坐标
        tx = x + next[k][0];
        ty = y + next[k][1];
        //判断越界
        if(tx<0 || ty<0 || tx>n-1 || ty>m-1)
            continue;
        //未走过的空地
        if(a[tx][ty] == '.') {
            a[tx][ty] = 'B'; //标记走过
            dfs(tx, ty); //递归
            a[tx][ty] = '.'; //取消标记
        }
    }
    return; //可去掉
}

完整代码1

bfs解题

#include<iostream>
#include<cstdio> //printf()
using namespace std;
struct note
{
    int x, y; //横纵坐标
};
char a[20][20]; //存储地图
int getnum(int i, int j) //统计四个方向的敌人
{
    int sum, x, y;
    sum = 0; //消灭敌人数
    x = i; y = j; //x,y临时变量
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            x--; //向上
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            x++; //向下
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            y--; //向左
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            y++; //向右
    }
    return sum;
}
int main()
{
    struct note que[401]; //20*20地图，队列扩展小于401
    int head, tail;
    int i, j, k, sum, Max = 0, mx, my, n, m, startx, starty, tx, ty;

    //定义方向数组
    int next[4][2] = {{-1,0}, {1,0}, {0,-1},{0,1}};
    cin>>n>>m>>startx>>starty; //n行m列
    for(i = 0; i < n; ++i) cin>>a[i];//读入n行字符

    //队列初始化
    head = 1; tail = 1;
    //插入起始坐标
    que[tail].x = startx;
    que[tail].y = starty;
    tail++;
    a[startx][starty] = 'B'; //标记走过
    Max = getnum(startx, starty); //起点消灭敌人数
    mx = startx; my = starty;
    //当队列不为空
    while(head < tail) {
        //枚举四个方向
        for(k = 0; k < 4; ++k) {
            tx = que[head].x + next[k][0];
            ty = que[head].y + next[k][1];
            //判断越界
            if(tx<0 || ty<0 || tx>n-1 || ty > m-1)
                continue;
            //判断未走过的平地
            if(a[tx][ty] == '.') {
                //每个点只入队一次
                a[tx][ty] = 'B'; //标记走过
                //新扩展的点插入队列
                que[tail].x = tx;
                que[tail].y = ty;
                tail++;
                //统计可消灭人数
                sum = getnum(tx, ty);
                //更新Max
                if(sum > Max) {
                    Max = sum;
                    mx = tx;
                    my = ty;
                }
            }
        }
        head++; //继续后面点的扩展
    }
    printf("将炸弹放在(%d, %d)处，可以消灭%d个敌人", mx,my,Max);
    return 0;
}

13 13 3 3
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.#.#
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
将炸弹放在(7, 11)处，可以消灭10个敌人

完整代码2

dfs解题

#include<iostream>
#include<cstdio> //scanf(),printf()
using namespace std;
char a[20][20]; //存储地图
int Max, mx, my, n, m; //声明为全局变量
int getnum(int i, int j) //统计四个方向的敌人
{
    int sum, x, y;
    sum = 0; //消灭敌人数
    x = i; y = j; //x,y临时变量
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            x--; //向上
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            x++; //向下
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            y--; //向左
    }
    x = i; y = j;
    while(a[x][y] != '#') {//不是墙
        if(a[x][y] == 'G') //是敌人
            sum++;
            y++; //向右
    }
    return sum;
}
void dfs(int x, int y)
{
    int k, sum, tx, ty;
    //计算人数
    sum = getnum(x, y);
    //更新值和坐标
    if(sum > Max)
    { Max = sum; mx = x; my = y; }
    //方向数组
    int next[4][2] = {{-1, 0},{1, 0},{0, -1},{0, 1}};
    //枚举四个方向
    for(k = 0; k < 4; ++k) {
        //下一节点坐标
        tx = x + next[k][0];
        ty = y + next[k][1];
        //判断越界
        if(tx<0 || ty<0 || tx>n-1 || ty>m-1)
            continue;
        //未走过的空地
        if(a[tx][ty] == '.') {
            a[tx][ty] = 'B'; //标记走过
            dfs(tx, ty); //递归
            a[tx][ty] = '.'; //取消标记
        }
    }
    return; //可去掉
}
int main()
{
    int i, startx, starty;
    cin>>n>>m>>startx>>starty; //n行m列
    for(i = 0; i < n; ++i) cin>>a[i];//读入n行字符

    a[startx][starty] = 'B';
    Max = getnum(startx, starty);
    mx = startx;
    my = starty;
    dfs(startx, starty);
    printf("炸弹放在(%d, %d),最多消灭%d个敌人",mx,my,Max);
    return 0;
}

输出同上 

总结

bfs核心是扩展，dfs核心是递归

仔细对比，其实本题中，bfs和dfs代码

相同点

1，方向数组next[4][2]        2,getnum()函数得到的消灭人数

区别

bfs构造完getnum()后，直接进入主函数，通过队列和开头的while(head < tail)得到答案

dfs构造完getnum()后，还要构造dfs()，这才进入主函数，然后调用函数得到答案 

bfs的主体是在主函数里通过队列实现的，dfs主体在主函数外通过递归实现 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/176134.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

04 |「链表」简析

04 |「链表」简析

前言 前言&#xff1a;研究一个数据结构的时候&#xff0c;首先讲的是增删改查。 文章目录前言一、链表简介1. 含义2. 节点组成3. 存储方式1&#xff09;数据在内存中的存储方式2&#xff09;单链表在内存中的存储方式3&#xff09;双链表在内存中的存储方式4&#xff09;循环链…
阅读更多...
python-38-降低内存开销的python迭代器

python-38-降低内存开销的python迭代器

【进阶Python】第五讲&#xff1a;迭代器与生成器 python 迭代器和生成器 迭代是Python中常用且非常强大的一个功能&#xff0c;它可以用于访问集合、列表、字符串、字典等数据结构的元素。 我们经常使用循环和条件语句&#xff0c;我们也清楚哪些是可以迭代访问&#xff0c;但…
阅读更多...
结构型模式-代理模式

结构型模式-代理模式

1.概述 由于某些原因需要给某对象提供一个代理以控制对该对象的访问。这时&#xff0c;访问对象不适合或者不能直接引用目标对象&#xff0c;代理对象作为访问对象和目标对象之间的中介。 Java中的代理按照代理类生成时机不同又分为静态代理和动态代理。静态代理代理类在编译…
阅读更多...
Nacos 配置中心源码讲解

Nacos 配置中心源码讲解

目录 1. 配置中心的优点 2. 配置模型结构 3. 配置中心 Server 端实现原理 3.1 新建配置 / 发布配置 3.2 查询配置 4. 配置中心 Client 端实现原理 4.1 发布配置 4.2 查询配置 4.3 监听机制 Listener 1. 配置中心的优点 运行时动态修改系统参数配置&#xff0c;不用重启…
阅读更多...
排序算法解析：快排，归并 （全）

排序算法解析：快排，归并 （全）

一、快排原始快排 算法思想&#xff1a;ps&#xff1a;排序的效果其实就是使一个数列中的每个数都满足左边数比它小、右边数比它大&#xff08;假设升序&#xff09;。接下来我们来了解快排&#xff1a;多次递归遍历&#xff0c;每单次遍历&#xff0c;设定一个限定值&#xff…
阅读更多...
02 |「数据结构、逻辑结构、物理结构」基本概念简析

02 |「数据结构、逻辑结构、物理结构」基本概念简析

前言 前言&#xff1a;简析数据结构、逻辑结构、物理结构。 文章目录前言一、数据结构1. 简介2. 数据3. 结构4. 分析5. 分类1&#xff09;线性结构&#xff08;线性表&#xff09;2&#xff09;树结构3&#xff09;图结构二、逻辑结构与物理结构1. 为什么要有逻辑结构和物理结构…
阅读更多...
SpringBoot+Vue--前端搭建-笔记1

SpringBoot+Vue--前端搭建-笔记1

前端搭建 首先安装node.js(百度) 官网下载地址&#xff1a;http://nodejs.cn/download 以前写的关于npm 后端了解的npm_biubiubiu0706的博客-CSDN博客 安装Node.js淘宝镜像加速器(cnpm) npm install cnpm -g(可以不安装) #建议使用如下语句解决npm速度慢的问题 好比设置仓…
阅读更多...
代码随想录算法训练营三期 day 24 - 回溯 (1) (补)

代码随想录算法训练营三期 day 24 - 回溯 (1) (补)

回溯算法理论基础 什么是回溯法 回溯法也可以叫做回溯搜索法&#xff0c;它是一种搜索的方式。回溯是递归的副产品&#xff0c;只要有递归就会有回溯。所以以下讲解中&#xff0c;回溯函数也就是递归函数&#xff0c;指的都是一个函数。 回溯法的效率 回溯的本质是穷举&…
阅读更多...
【手把手教你学51单片机】中断的优先级

【手把手教你学51单片机】中断的优先级

注&#xff1a;本文章转载自《手把手教你学习51单片机》&#xff01;因转载需要原文链接&#xff0c;故无法选择转载&#xff01; 如若侵权&#xff0c;请联系我进行删除&#xff01;上传至网络博客目的为了记录自己学习的过程的同时&#xff0c;同时能够帮助其他一同学习的小伙…
阅读更多...
第四十三章 动态规划——最长单调序列模型

第四十三章 动态规划——最长单调序列模型

第四十三章 动态规划——最长单调序列模型一、最长单调序列模型1、模型母题2、思路分析&#xff08;两种方法&#xff1a;DP&#xff0c;贪心&#xff09;二、模型的应用1、AcWing 1017. 怪盗基德的滑翔翼&#xff08;1&#xff09;问题&#xff08;2&#xff09;分析&#xff…
阅读更多...
C规范编辑笔记(十四)

C规范编辑笔记(十四)

往期文章&#xff1a; C规范编辑笔记(一) C规范编辑笔记(二) C规范编辑笔记(三) C规范编辑笔记(四) C规范编辑笔记(五) C规范编辑笔记(六) C规范编辑笔记(七) C规范编辑笔记(八) C规范编辑笔记(九) C规则编辑笔记(十) C规范编辑笔记(十一) C规范编辑笔记(十二) C规范编辑笔记(…
阅读更多...
Linux进程学习【一】

Linux进程学习【一】

✨个人主页&#xff1a; Yohifo &#x1f389;所属专栏&#xff1a; Linux学习之旅 &#x1f38a;每篇一句&#xff1a; 图片来源 &#x1f383;操作环境&#xff1a; CentOS 7.6 阿里云远程服务器 Perseverance is not a long race; it is many short races one after another…
阅读更多...
Linux基本功系列之rename命令实战

Linux基本功系列之rename命令实战

文章目录一. rename 命令介绍二. 语法格式及常用选项三. 参考案例3.1 将当前目录下所有.cfg的文件&#xff0c;替换为.txt结尾3.2 将所有出现mufeng的部分都替换为mufeng13.3 将mufeng0开头都变成mufeng00开头3.4 rename支持正则表示式总结前言&#x1f680;&#x1f680;&…
阅读更多...
2023-1-22 刷题情况

2023-1-22 刷题情况

积水面积 先祝大家新年快乐&#xff0c;新的一年&#xff0c;万事如意。 题目描述 一组正整数&#xff0c;分别表示由正方体叠起的柱子的高度。若某高度值为 xxx&#xff0c;表示由 xxx 个正立方的方块叠起&#xff08;如下图&#xff0c;0≤x≤50000 \le x \le 50000≤x≤5…
阅读更多...
卷积神经网络进阶--基础知识

卷积神经网络进阶--基础知识

卷积神经网络进阶 b站课程链接碳基生物都能学会的神经网络&#xff08;跳着看的&#xff09; 因为我用的是pytorch&#xff0c;而该课程是用tenserflow的&#xff0c;所以主要记了一下理论 为什么要讲不同的网络结构 不同的网络结构解决的问题不同不同的网络结构使用的技巧不同…
阅读更多...
【人工智能原理自学】卷积神经网络：打破图像识别的瓶颈

【人工智能原理自学】卷积神经网络：打破图像识别的瓶颈

&#x1f60a;你好&#xff0c;我是小航&#xff0c;一个正在变秃、变强的文艺倾年。 &#x1f514;本文讲解卷积神经网络&#xff1a;打破图像识别的瓶颈&#xff0c;一起卷起来叭&#xff01; 目录一、手写体识别二、“炼丹”一、手写体识别 在机器学习、神经网络领域&#…
阅读更多...
【数据分析】(task4)数据可视化

【数据分析】(task4)数据可视化

note matplotlib的四个容器&#xff1a; Figure&#xff1a;顶层级&#xff0c;用来容纳子 Axes&#xff0c;一组具体绘图元素和画布&#xff08;canvas&#xff09;。 画板。Axes&#xff1a;matplotlib宇宙的核心&#xff0c;容纳了大量元素用来构造一幅幅子图&#xff0c;一…
阅读更多...
【QT5.9】与MFC对比学习笔记-感悟篇【2023.01.22】

【QT5.9】与MFC对比学习笔记-感悟篇【2023.01.22】

简介 在公司从事MFC的程序维护一年两个月&#xff0c;期间因为公司被QT告侵权对QT产生了抵触的心情。现在无奈要用到&#xff0c;需要抓紧学习了。 正文 1.数据模型 先说下刚用到的模型&#xff0c;模型也叫数据模型&#xff0c;也就是耳熟的MVC架构中的M&#xff08;Model…
阅读更多...
我用笨办法啃下了一个开源项目的源码！

我用笨办法啃下了一个开源项目的源码！

目录 1、从最简单的源码开始&#xff1a;别幻想一步登天 2、循序渐进&#xff1a;先搞定底层依赖的技术 3、一定要以Hello World作为入口来阅读 4、抓大放小&#xff0c;边写注释边画图 5、反复三遍&#xff0c;真正理解源码 6、借力打力&#xff0c;参考源码分析书籍及博客 7…
阅读更多...
研一寒假C++复习笔记--引用的使用

研一寒假C++复习笔记--引用的使用

​​​​​​​ 目录 1--引用的基本语法 2--引用的注意事项 3--在函数参数中使用引用 4--引用作函数的返回值 5--引用的本质 6--常量引用 1--引用的基本语法 引用相当于给变量起别名&#xff0c;其基本语法如下&#xff1a; 数据类型 &别名 原名 # include <…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023