最少侧跳次数

难度：中等

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

• 比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

• 比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。

这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意： 点 0 处和点 n 处的任一跑道都不会有障碍。

示例 1：

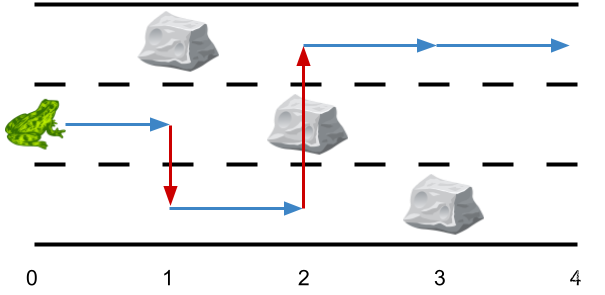
输入：obstacles = [0,1,2,3,0]
输出：2 
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

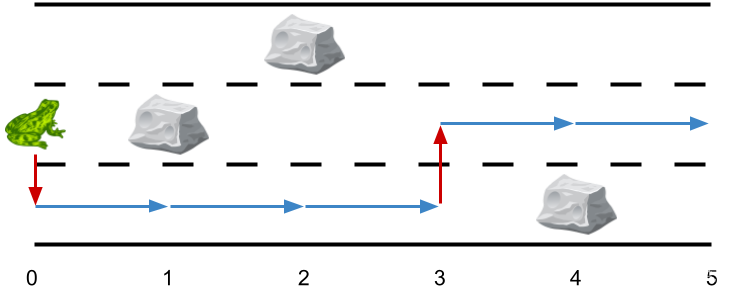
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

贪心

思路：

1. 基于贪心的思想，当前赛道里面一直往前跑，直到遇到障碍物停下来。
2. 其他两个赛道也基于贪心的思想，比较一下可以跑的最远距离，选择可以跑得最远的那个赛道。
3. 循环1和2步骤，一直到达终点结束程序。

复杂度分析：

• 时间复杂度： $O(n)$， 最坏的情况，每两次跳一次，每次查询只会查询2个长度，也就是 $O(n+2n)$，所以最终时间复杂度是$O(n)$。
• 空间复杂度： $O(1)$， 使用常数个变量。

class Solution:
    def minSideJumps(self, obstacles) -> int:
        track, length, res = 2, 0, 0
        while length < len(obstacles) - 1:
        	# 遇到障碍物停下来抉择
            if obstacles[length + 1] == track:
            	# 可能跳的另外两个赛道
                track_1 = (track + 1) % 3 if track + 1 > 3 else track + 1
                track_2 = (track + 2) % 3 if track + 2 > 3 else track + 2
                index, track = length, track_1
                # 选择可以跑得最远的那个赛道
                while index < len(obstacles):
                    if obstacles[index] == track_1:
                        track = track_2
                        break
                    elif obstacles[index] == track_2:
                        break
                    index += 1
                res += 1
            length += 1
        return res

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-sideway-jumps