目录

一、希尔伯特（Hilbert）矩阵

二、托普利兹（Toeplitz）矩阵

三、0～1间均匀分布的随机矩阵

四、标准正态分布随机矩阵

五、魔方矩阵

六、帕斯卡矩阵

七、范德蒙（Vandermonde）矩阵

---

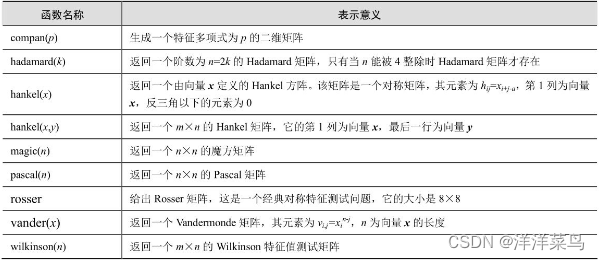
MATLAB中生成特殊矩阵的部分函数：

一、希尔伯特（Hilbert）矩阵

希尔伯特（Hilbert）矩阵，也称H阵，其元素为Hij=1/(i+j-1)。由于它是一个条件数差的矩阵，所以将它用来作为试验矩阵。

关于希尔伯特矩阵的指令函数如下：

1. hilb(n)：用于生成一个n×n的希尔伯特矩阵。
2. invhilb(n)：用于生成一个n×n的希尔伯特矩阵的逆矩阵整数矩阵。

示例1：生成3*3希尔伯特矩阵

A=hilb(3) %3*3希尔伯特矩阵

运行结果：

示例2：生成3*3希尔伯特矩阵的逆矩阵整数矩阵

B=invhilb(3) %希尔伯特矩阵的逆矩阵整数矩阵

运行结果：

二、托普利兹（Toeplitz）矩阵

托普利兹（Toeplitz）矩阵由两个向量定义，一个行向量和一个列向量。对称的托普利兹矩阵由单一向量来定义。

关于托普利兹矩阵的指令函数如下：

1. toeplitz(k,r)：用于生成非对称托普利兹矩阵，第1列为k，第1行为r，其余元素等于其左上角元素。
2. toeplitz(c)：用于用向量c生成一个对称的托普利兹矩阵。

示例3：生成托普利兹矩阵

C=toeplitz(2:5,2:2:8)

运行结果：

三、0～1间均匀分布的随机矩阵

在MATLAB中常用rand()函数产生0～1间均匀分布的随机矩阵，其调用格式如下：

1. r = rand(n)：产生维数为n×n的0～1间均匀分布的随机矩阵。
2. r = rand(m,n)：产生维数为n×m的0～1间均匀分布的随机矩阵。
3. r = rand(m,n,p,...)：产生维数为n×m×p的0～1间均匀分布的随机矩阵。
4. r = rand(size(A))：产生维数为n×m×p与矩阵A相同的0～1间均匀分布的随机矩阵。

示例4：生成0～1间均匀分布的随机矩阵

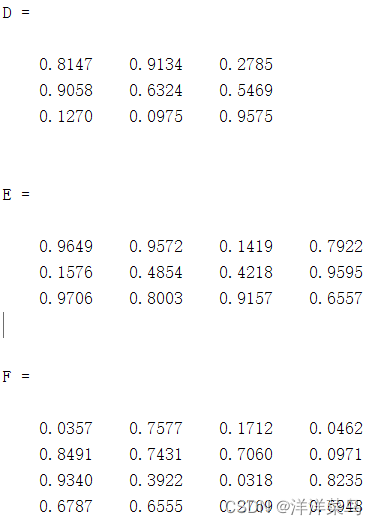
D=rand(3)

E=rand([3,4])

F=rand(size(C))

运行结果：

四、标准正态分布随机矩阵

在MATLAB中常用randn()函数产生均值为0、方差为1的随机矩阵，其调用格式如下：

1. r = randn(n)。
2. r = randn(m,n)。
3. r = randn(m,n,p,...)。
4. r = randn([m,n,p,...])。
5. r = randn(size(A))。
6. 其格式可参考上述rand()函数。

示例5：生成标准正态分布随机矩阵

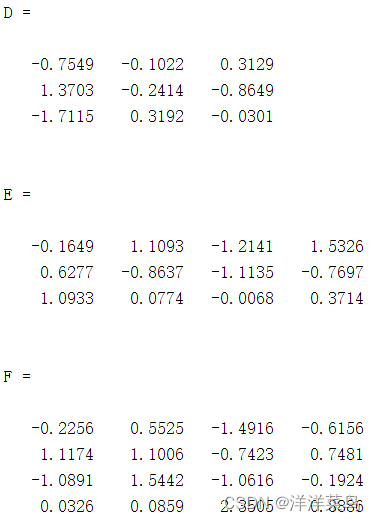
D=randn(3)

E=randn([3,4])

F=randn(size(C))

运行结果：

五、魔方矩阵

在MATLAB中常用magic()函数产生魔方矩阵。魔方矩阵中每行、列和两条对角线上的元素和相等，其调用格式如下：

1. M= magic(n)。

示例6：生成魔方矩阵

A=magic(3)

B=magic(4)

C=magic(5)

D=sum(A)

E=sum(A')

运行结果：

六、帕斯卡矩阵

在MATLAB中常用pascal()函数产生帕斯卡矩阵，其调用格式如下：

1. A=pascal(n) ：返回n阶的对称正定Pascal矩阵，其中的元素是由Pascal三角组成的，其逆矩阵的元素都是整数。
2. A = pascal(n,1)：返回由下三角的Cholesky因子组成的Pascal矩阵，它是对称的，所以它是自己的逆。
3. A = pascal(n,2)：返回pascal(n,1)的转置和交换形式。A是单位矩阵的立方根。

示例7：生成帕斯卡矩阵

A=pascal(4)

B=pascal(3,2)

运行结果：

七、范德蒙（Vandermonde）矩阵

在MATLAB中常用vander()函数产生范德蒙矩阵，其调用格式如下：

1. A = vander(v)：生成范德蒙矩阵，矩阵的列是向量v的幂，即A(i,j)=v(i)^(n-j)，其中n=length (v)。

示例8：生成范德蒙（Vandermonde）矩阵

A=vander([1 2 3 4])

B=vander([1;2;3;4])

C=vander(1:.5:3)

运行结果：

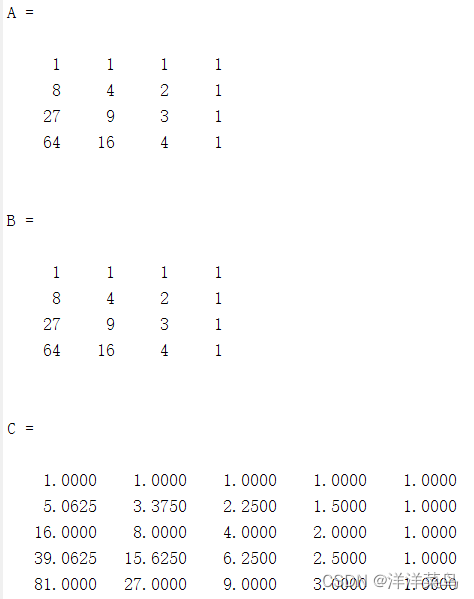
注意：vander()函数产生范德蒙矩阵，输入向量可以使行向量或列向量。