今年是农历腊月二十九，提前祝大家新春快乐。这是我壬寅虎年最后一篇文章，感谢大家的阅读。祝大家兔年吉祥，身体健康、阖家幸福、学业有成、事业如意、财源滚滚！

前置说明

本文中所有用到的二叉树及二叉树节点，都是由下面的代码定义创建的：

typedef int BTDataType;  //二叉树存储的数据类型

//二叉树节点
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;   //左子树
	struct BinaryTreeNode* right;  //右子树
}BTNode;  //将二叉树节点结构体类型重定义为BTNode

将二叉树中存储的数据的类型重定义为BTDataType，二叉树节点定义为结构体类型数据，结构体成员包括：存储的数据data、指向其左孩子节点的指针left、指向其右孩子节点的指针right，将二叉树节点结构体类型重定义为BTNode。

问题1. 统计二叉树节点个数

1.1 问题描述

设计函数int BinaryTreeSize(BTNode* root)，统计一颗二叉树中有几个节点，其中函数的参数root为指向根节点的指针，函数二叉树返回节点个数。

如图1.1所示二叉树，节点个数为6。

1.2 解题思路

本题采用递归的思想来解决（见图1.2）

1. 判断传入函数的根节点指针是否为NULL，如果是，则函数返回0。
2. 如果根节点指针不是NULL，则将root的左孩子节点和右孩子节点作为参数传给函数BinaryTreeSize递归调用，函数返回1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right)，即：左子树节点数 + 右子树节点数 + 1。

1.3 函数代码

//统计二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (NULL == root)
		return 0;

	//计入root节点。然后再递归调用函数计算左右子树的节点个数
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

问题2. 统计二叉树中叶子节点的个数

2.1 问题描述

设计函数int BinaryTreeLeafSize(BTNode* root)，统计一颗二叉树中叶子结点的个数。叶子节点就是左孩子节点和右孩子节点均为空的节点。

如图1.1所示的二叉树，其叶子节点为D、E、F，叶子节点个数为3。

2.2 解题思路

通过递归的思想解决问题（见图2.1）

1. 判断传入函数的根节点root是否为NULL，如果是，则表示树为空，函数返回NULL。
2. 在root不为空的前提下，判断root的左孩子节点和右孩子节点是否均为NULL，如果均为NULL，则证明root表示的节点为叶子节点，函数返回1。
3. 若root既不是NULL也不是叶子节点，则统计以root为根节点的左右子树共有几个叶子节点，函数返回BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right)。

2.3 函数代码

//统计二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (NULL == root)
		return 0;

	//如果root的左孩子节点和右孩子节点均为NULL，则root为叶子结点
	if (root->left == NULL && root->right == NULL)
		return 1;

	//root不是NULL也不是叶子节点
	//统计root的左子树中叶子节点个数和右子树中叶子节点个数并相加
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

问题3. 统计二叉树中第k层节点个数 

3.1 问题描述

以根节点为二叉树的第一层，设计函数int BinaryTreeLevelKSize(BTNode* root, int k)，统计第k层有几个节点，如图3.1所示的二叉树，其第1、2、3层的节点个数为分别为1、2、3。

3.2 解题思路

统计二叉树中第k层节点数，可以转化为统计二叉树的左子树和右子树第k-1层的节点个数之和，并最终转换为计算第k-1层所有节点的孩子节点个数之和。通过递归的思想来解决问题（见图3.2）。

1. 判断root是否为空，如果为空，则函数返回NULL。
2. 判断root是否为第k层的节点（k==1是否成立），如果是，则函数返回1。
3. 如果root既不为空也不是第k层的节点，则统计其左子树和右子树第k-1层节点的个数之和，即函数返回BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root -> right, k-1)。

3.3 函数代码

//统计二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BinaryTreeLevelKSize(root->left, k - 1) 
		+ BinaryTreeLevelKSize(root->right, k - 1);
}

问题4. 查找二叉树中值为x的节点

4.1 问题描述

设计函数BTNode* BinaryTreeFind(BTNode* root, BTDataType x)，在一颗二叉树中查找值为x的节点。如果查找到了这样的一个节点，就返回指向这个节点的指针，如果没有找到，函数返回NULL。

4.2 解题思路

采用递归的思想，按照前序遍历的方法，依次将每一个节点的值与x比较，如果相同，就返回该节点的地址，具体步骤为：

1. 判断root是否为NULL，如果是，则返回NULL。
2. 判断根节点root的数据是否为x，如果是，返回root。
3. 若干root既不是NULL，其节点值也不是x，将root->left作为第一个参数传给BinaryTreeFind函数递归调用，查找其左子树中是否存在x，如果存在，函数返回值为x的节点，函数不再走步骤4。
4. 如果左子树中未找到x，那么再将root->right作为第一个参数传给函数BinaryTreeFind递归调用，查找右子树中是否存在x。如果存在，函数返回值为x节点的地址，如果不存在，则表明二叉树中没有x，函数返回NULL。

4.3 函数代码

//查找二叉树中值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	//根节点值为x，直接返回根节点地址
	if (root->data == x)
	{
		return root;
	}

	//根节点值不为x，去左子树查找
	BTNode* LeftFind = BinaryTreeFind(root->left, x);
	if (LeftFind)
	{
		return LeftFind;
	}

	//根节点值不为x且左子树中没有x，查找右子树
	BTNode* RightFind = BinaryTreeFind(root->right, x);
	if (RightFind)
	{
		return RightFind;
	}

	return NULL;
}

问题5. 判断一颗二叉树是否为单值二叉树

5.1 问题描述

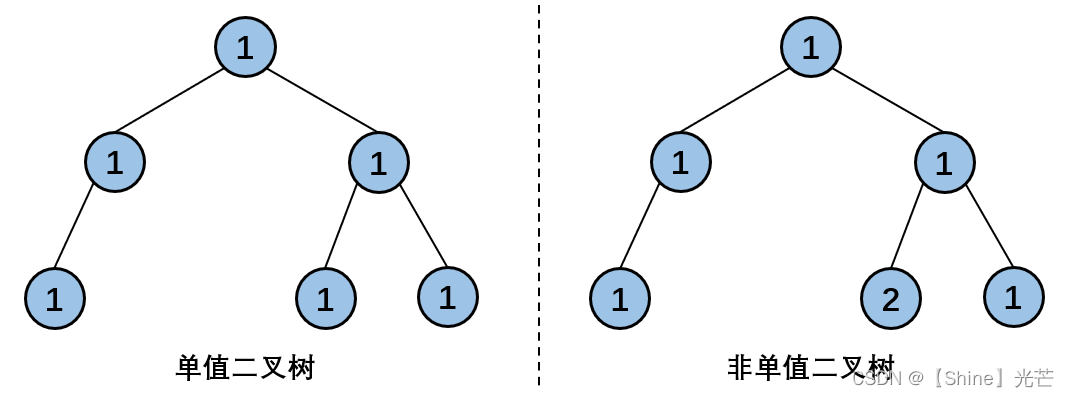
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树，如图5.1，图中左边二叉树是单值二叉树，右边二叉树不是单值二叉树。设计函数bool isUnivalTree(struct TreeNode* root)，判断一颗二叉树是否为单值二叉树。

5.2 解题思路 

本题采用递归的思想，对于作为参数传给函数的根节点，依次比较其左孩子节点的值和右孩子节点的值是否与根节点值相等，如果一颗二叉树所有非叶子节点的左右孩子节点的值都与节点本身值相等，则该二叉树为单值二叉树。

1. 判断root是否为NULL，如果是，函数返回true。
2. 如果root的左孩子节点root->left不为空且其值与root的值不同，函数返回false。
3. 如果root的右孩子节点root->right不为空且其值与root的值不同，函数返回false。
4. 如果函数走到这一步，说明root的左右孩子节点都存在且值都与root的值相同，则通过递归判断root的左子树和右子树是否为单值二叉树，如果root的左右子树都是单值二叉树，则整颗二叉树为单值二叉树，函数返回true，否则返回false。

5.3 函数代码

bool isUnivalTree(struct TreeNode* root)
{
    if(NULL == root)
    {
        return true;
    }

    //左孩子不为空且值与根节点不同
    if(root->left && root->left->val != root->val)
    {
        return false;
    }

    //右孩子不为空且值与根节点不同
    if(root->right && root->right->val != root->val)
    {
        return false;
    }

    //递归，判断左右子树是否均为单值二叉树
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

问题6. 判断两颗二叉树是否相同

6.1 问题描述

设计函bool isSameTree(struct TreeNode* p, struct TreeNode* q)，判断两颗二叉树是否相同，p和q为两颗二叉树的根节点。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。图6.1和图6.2分别展示了两颗相同的二叉树和两颗不同的二叉树。

6.2 解题思路

按照前序遍历，依次比较两颗二叉树的每一个节点，两颗二叉树的结构和每个节点值均相同，则两个二叉树相同。这里采用递归的思想，先比较两颗二叉树的根节点是否相同，如果相同，在先后比较这两个二叉树的左子树和右子树是否相同，如果两颗二叉树的左右子树均相同，则这两颗二叉树相同。

1. 判断p和q是否均为空，如果均为空，返回true。
2. 判断两颗二叉树结构是否相同，即：判断p和q是否一个为空另一个不为空。如果一个为空另一个不为空，则两颗二叉树结构不同，函数返回false。
3. 判断p节点和q节点值是否相同，如果不同，函数返回false。
4. 比较两个数的左右子树是否相同，函数返回isSameTree(p->left, q->left) && isSameTree(p->right, q->right)，即：两颗左右子树如果分别相同，则两个二叉树相同，函数返回true，否则两颗二叉树不同，函数返回false。

6.3 函数代码

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    //p和q都为空，返回真
    if(p == NULL && q == NULL)
    {
        return true;
    }

    //p和q一个为空一个不为空，返回假
    if(p == NULL || q == NULL)
    {
        return false;
    }

    //p和q都不为空，但值不一样，返回假
    if(p->val != q->val)
    {
        return false;
    }

    //递归调用，比较左右子树是否相同
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

问题7. 判断一颗二叉树是否为对称二叉树

7.1 问题描述

给定二叉树根节点root，设计函数bool isSymmetric(struct TreeNode* root)，判断二叉树是否为对称二叉树，图7.1展示了对称二叉树和非对称二叉树。

7.2 解题思路

如果一颗二叉树是对称二叉树，那么它应该满足下面的条件：

• 两棵树的根节点值相同
• 每棵树的右子树都与另一颗树的左子树镜像对称

综上，本题可以采用递归的思想，定义两个二叉树节点指针root1和root2，当root1向其左子树方向移动时，root2向其右子树方向移动，当root1向其右子树方向移动时，root2向其左子树方向移动。每次检查当前root1和root2节点的值是否相等，如果相等再判断左右子树是否对称。

为此，应当再定义一个子函数bool check_val(struct TreeNode* root1, struct TreeNode* root2)，用于检查节点root1和root2节点值是否相等，然后检查root1的左子树与root2的右子树是否镜像对称，root1的右子树与root2的左子树是否镜像对称。

7.3 函数代码

//定义两个节点root1和root2
//root1左移，root2就右移；root1右移，root2就左移
//检查p和q的值是否相同
bool check_val(struct TreeNode* root1, struct TreeNode* root2)
{
    //两节点都为NULL，返回true
    if(root1 == NULL && root2 == NULL)
    {
        return true;
    }

    //一个节点是NULL另一个节点不是，不对称，返回false
    if(root1 == NULL || root2 == NULL)
    {
        return false;
    }

    //检查两节点值是否相同以及左右子树的镜像对称情况
    return (root1->val == root2->val) 
            && check_val(root1->left, root2->right)
            && check_val(root1->right, root2->left);
}

bool isSymmetric(struct TreeNode* root)
{
    if(NULL == root)
    {
        return true;
    }

    //检查左右子树是否镜像对称
    return check_val(root->left, root->right);  //值检查函数
}

问题8. 判断一颗二叉树是否为另一颗二叉树的子树

8.1 问题描述

给定两棵二叉树root和subRoot，设计函数bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)，判断二叉树root中是否存在子树subRoot，二叉树的一棵子树包括的某个节点和这个节点的所有后代节点。图8.1中二叉树subRoot为二叉树root的一颗子树。

8.2 解题思路

• 思路：转化为子树是否相等的问题

通过前序遍历遍历二叉树的每一个节点，当root的值与subRoot的值相同时，调用函数isSameTree，判断以root节点为根节点的子树与subRoot是否为相同的二叉树，如果是相同的二叉树，函数返回true，如果不是相同的二叉树，继续比较二叉树root的剩余节点的值与subRoot的根节点值是否相同以寻找子树subRoot，直到二叉树root的所有节点均被遍历或找到子树subRoot为止。

8.3 函数代码

isSameTree函数的代码见6.3节。

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    //根和子根均为空，返回true
    if(!root && !subRoot)
    {
        return true;
    }

    //两者之一为空返回假
    if(!root || !subRoot)
    {
        return false;
    }

    //树和子树根节点值相同，检查两树是否相同
    if(root->val == subRoot->val)
    {
        bool ret = isSameTree(root, subRoot);
        if(ret)
        {
            return ret;
        }
    }

    //检查左子树和右子树是否与subRoot相同
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

问题9. 二叉树的销毁

9.1 问题描述

设计函数void BinaryTreeDestory(BTNode** root)，释放创建二叉树时，为二叉树每一个节点动态申请的内存空间，并将指向根节点的指针置为NULL。

9.2 解题思路

通过后序遍历释放依次释放一颗二叉树的左子树节点、右子树节点和根节点，最后通过对二级指针root的解引用，将指向根节点的指针置为NULL。

这里采用后序遍历销毁二叉树时为了避免根节点释放后无法找到其左孩子节点和右孩子节点的问题。

9.3 函数代码

//二叉树销毁函数
void BinaryTreeDestory(BTNode** root)
{
	if (NULL == *root)
		return;

	//销毁左子树
	BinaryTreeDestory(&(*root)->left);
	//销毁右子树
	BinaryTreeDestory(&(*root)->right);
	//销毁根节点
	free(*root);

	*root = NULL;
}

问题10. 判断一颗二叉树是否为完全二叉树

10.1 问题描述

给定一个二叉树根节点root，设计函数bool BinaryTreeComplete(BTNode* root)，判断该二叉树是否为完全二叉树，如果是函数返回true，否则函数返回false。

完全二叉树概念：对于一颗深度为h的二叉树，其前h-1层节点个数均达到最大值，第h层节点个数可能没有达到最大值，但从左到右是连续的。

10.2 解题思路

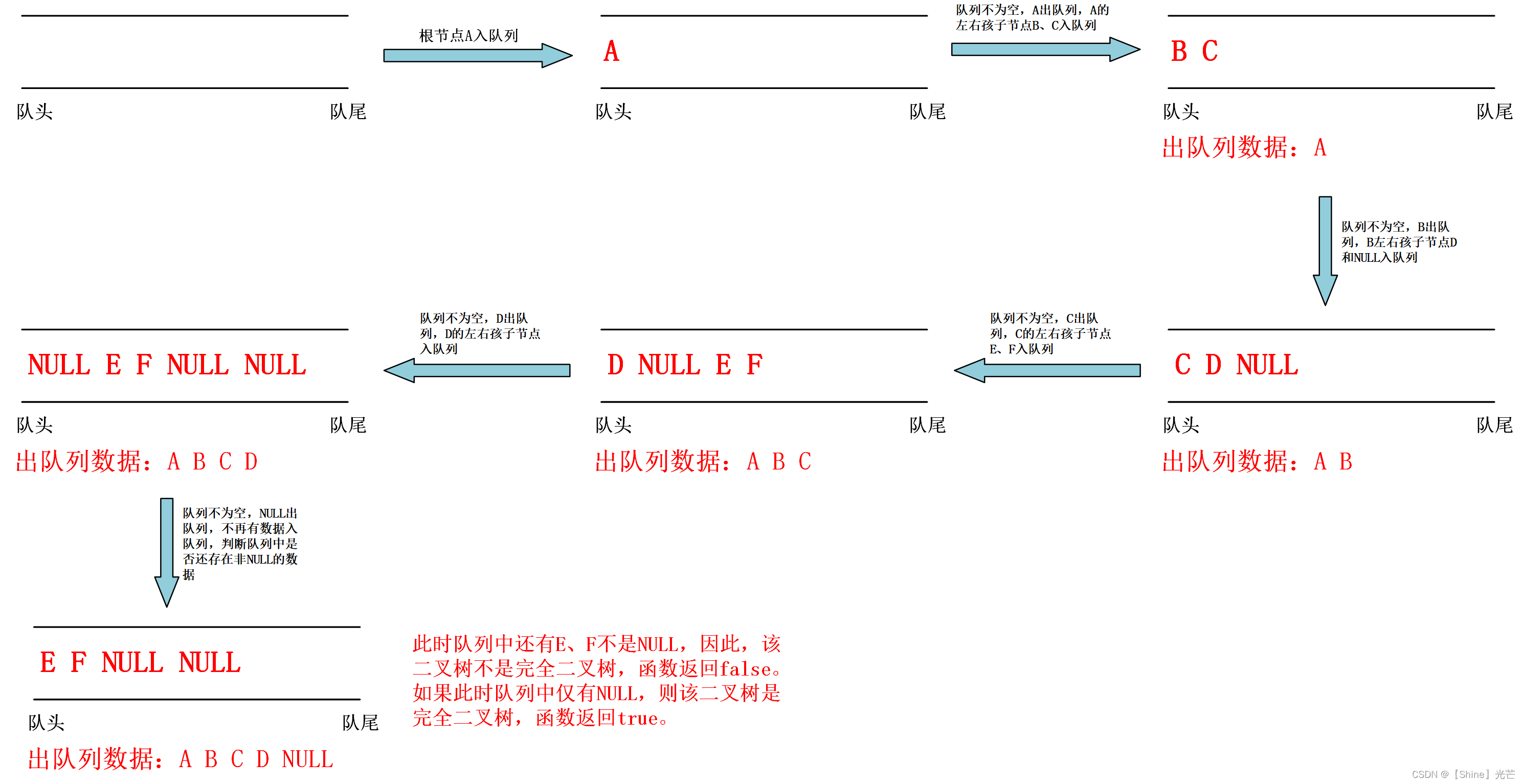
判断完全二叉树的解题思路与层序遍历类似，均需要借助队列来实现目的。

1. 创建队列，让根节点入队列。
2. 当队列不为空时，提取队列队首数据。如果队首为NULL，则检查队列中是否还存在不为NULL的数据，如果存在，那么该二叉树不是完全二叉树如果不存在，则是完全二叉树。
3. 如果队首不是NULL，则让队首数据节点的左孩子节点和右孩子节点先后入队列。注意：对于层序遍历，孩子节点不为空才入队列，对于判断完全二叉树的问题，无论孩子节点是否为NULL，都要入队列。

10.3 函数代码

bool BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;

	Queue q;  //创建队列
	QueueInit(&q);  //初始化队列
	QueuePush(&q, root);  //根节点入队列

	while (!QueueEmpty(&q))  //队列不为空
	{
		BTNode* front = QueueFront(&q);  //提取队首数据
		QueuePop(&q);  //删除队首数据

		if (front == NULL)
		{
			//队首为空，终止循环
			break;
		}
		else
		{
			//front的左右孩子节点无论是否为NULL，均入队列
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	//队首遇到空，判断队列中是否还存在不为NULL的数据
	//1.如果存在，表明不是完全二叉树
	//2.如果不存在，表明是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}