链表的算法题

news2024/10/5 21:14:16

目录

题型一、克隆含有rand指针的链表

笔试：哈希表

面试：不用容器，模拟哈希表的功能

题型二、给一个单链表头节点Head，判断是否构成回文

题型三、将单链表按某值划分为左边小，中间相等，右边大

6个变量，不用容器，还能保证稳定性

题型四、找到两条链表的第一个相交节点

1、先找到两个链表的入环节点

2、接下来分情况讨论

题型五、不给头节点，要求删一个给定的节点 ？

 1、小聪明法：借尸还魂

对于笔试：不用太在乎空间复杂度，一切为了时间复杂度。

对于面试：时间复杂度依然放在第一位，但一定要找到空间最省的办法。

题型一、克隆含有rand指针的链表

 

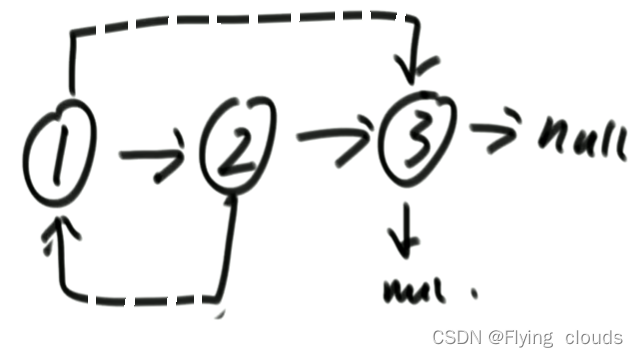
笔试：哈希表

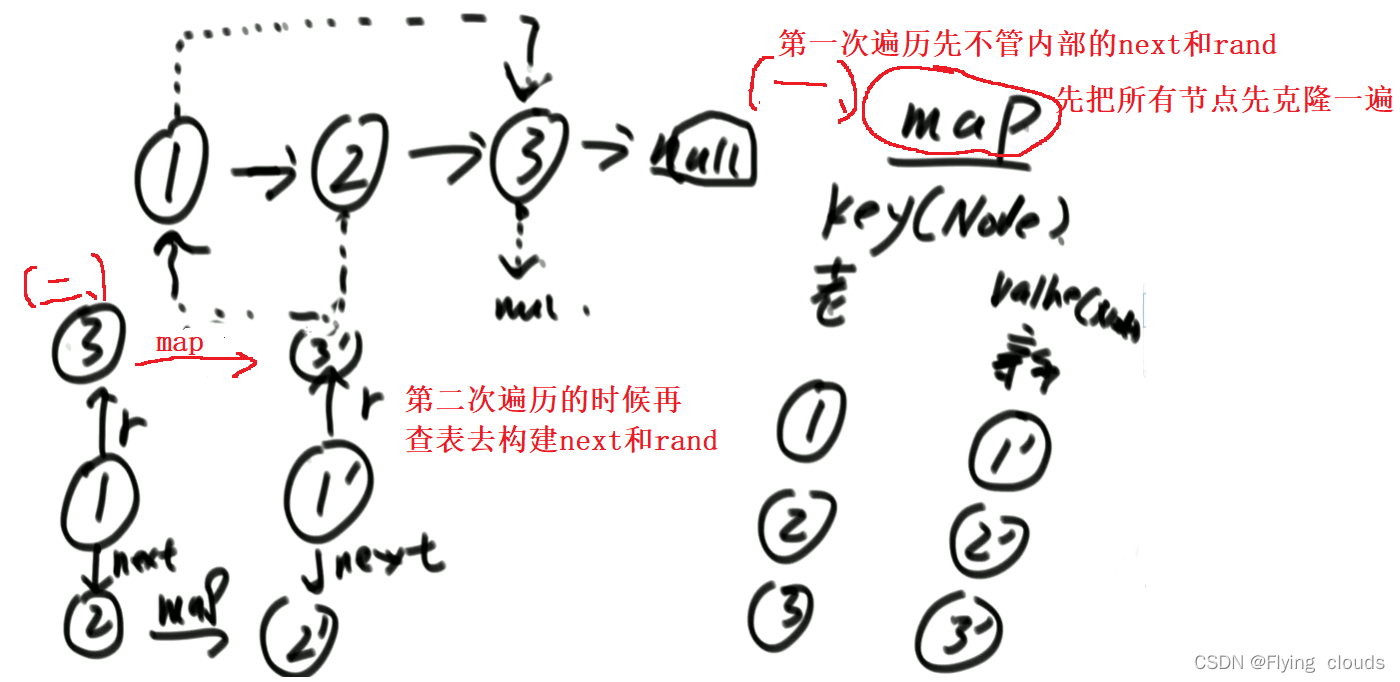
 代码：

	Node* Hashfunc(Node* head)
	{
		unordered_map<Node*,Node*> Node_map;
		Node* cur = head;
		while (cur!= nullptr)
		{
			Node* new_cur = new Node(cur->value);
			
			Node_map.insert(make_pair(cur, new_cur));
			cur = cur->next;
		}
		cur = head;
		while (cur != nullptr)
		{
			Node_map.find(cur)->second->next = cur->next;
			Node_map.find(cur)->second->rand = cur->rand;
			cur = cur->next;
		}
		return Node_map.find(head)->second;
	}

面试：不用容器，模拟哈希表的功能

	Node* copyRandomList2(Node* head) {
		if (head == nullptr) {
			return nullptr;
		}
		Node* cur = head;
		Node* next = nullptr;
		// 1 -> 2 -> 3 -> nullptr
		// 1 -> 1' -> 2 -> 2' -> 3 -> 3'
		while (cur != nullptr) {
			next = cur->next;
			cur->next = new Node(cur->value);
			cur->next->next = next;
			cur = next;
		}
		cur = head;
		Node* copy = nullptr;
		// 1 1' 2 2' 3 3'
		// 依次设置 1' 2' 3' random指针
		while (cur != nullptr) {
			next = cur->next->next;
			copy = cur->next;
			copy->rand = cur->rand != nullptr ? cur->rand->next : nullptr;
			cur = next;
		}
		Node* res = head->next;
		cur = head;
		// 老 新 混在一起，next方向上，random正确
		// next方向上，把新老链表分离
		while (cur != nullptr) {
			next = cur->next->next;
			copy = cur->next;
			cur->next = next;
			copy->next = next != nullptr ? next->next : nullptr;
			cur = next;
		}
		return res;
	}

题型二、给一个单链表头节点Head，判断是否构成回文

笔试：

依次遍历，放于栈中，然后再弹出去对比

面试：

1.先通过快慢指针找到中间的节点，中间节点的next指向null

2.然后再把后半部分给逆序一下，并保存最后一个节点，

3.逆序以后再从L和R依次遍历比较，有不相同的就返回

4.不管满足不满足回文，最后一定要记得把链表的结构给恢复原状

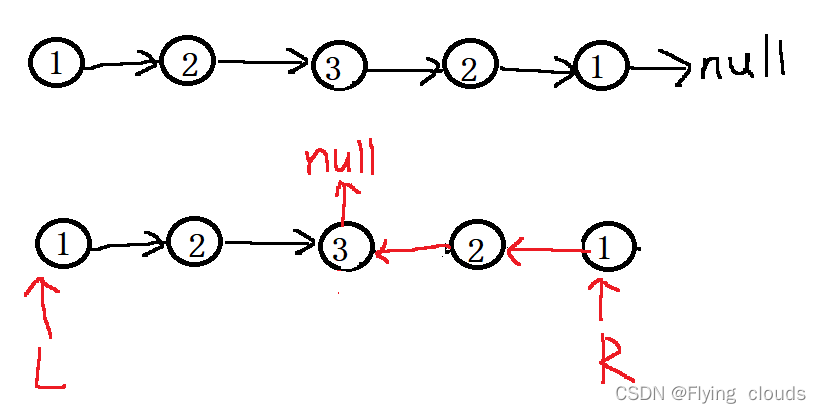
 代码实现：

class FindLink_Mid;
class Node
{
	friend class FindLink_Mid;
public:
	Node(int v)
	{
		value = v;
	}
private:
	int value;	
	Node* next;
};

class FindLink_Mid
{

public:
	//奇数返回中点偶数返回上中点
	Node* midOrUpMidNode(Node* head) 
	{
		if (head == nullptr || head->next == nullptr || head->next->next == nullptr) {
			return head;
		}
		// 链表有3个点或以上
		Node* slow = head->next;
		Node* fast = head->next->next;
		while (fast->next != nullptr && fast->next->next != nullptr) 
		{
			slow = slow->next;
			fast = fast->next->next;
		}
		return slow;
	}
	//奇数返回中点，偶数返回下中点
	Node* midOrDownMidNode(Node* head) 
	{
		if (head == nullptr || head->next == nullptr) 
		{
			return head;
		}
		Node* slow = head->next;
		Node* fast = head->next;
		while (fast->next != nullptr && fast->next->next != nullptr)
		{
			slow = slow->next;
			fast = fast->next->next;
		}
		return slow;
	}
	//奇数返回中点前一个，偶数返回上中点前一个
	Node* midOrUpMidPreNode(Node* head) {
		if (head == nullptr || head->next == nullptr || head->next->next == nullptr)
		{
			return nullptr;
		}
		Node* slow = head;
		Node* fast = head->next->next;
		while (fast->next != nullptr && fast->next->next != nullptr)
		{
			slow = slow->next;
			fast = fast->next->next;
		}
	}

	//奇数返回中点前一个，偶数返回下中点前一个
	Node* midOrDownMidPreNode(Node* head) 
	{
		if (head == nullptr || head->next == nullptr)
		{
			return head;
		}
		if (head->next->next == nullptr)
		{
			return head;
		}
		Node* slow = head;
		Node* fast = head->next;
		while (fast->next != nullptr && fast->next->next != nullptr) {
			slow = slow->next;
			fast = fast->next->next;
		}
		return slow;
	}

};

题型三、将单链表按某值划分为左边小，中间相等，右边大

笔试：

把链表放在数组中，然后再去partition

面试：

6个变量，不用容器，还能保证稳定性

流程示意图：

我们要先构造三个区域，然后再把三个区域给串起来

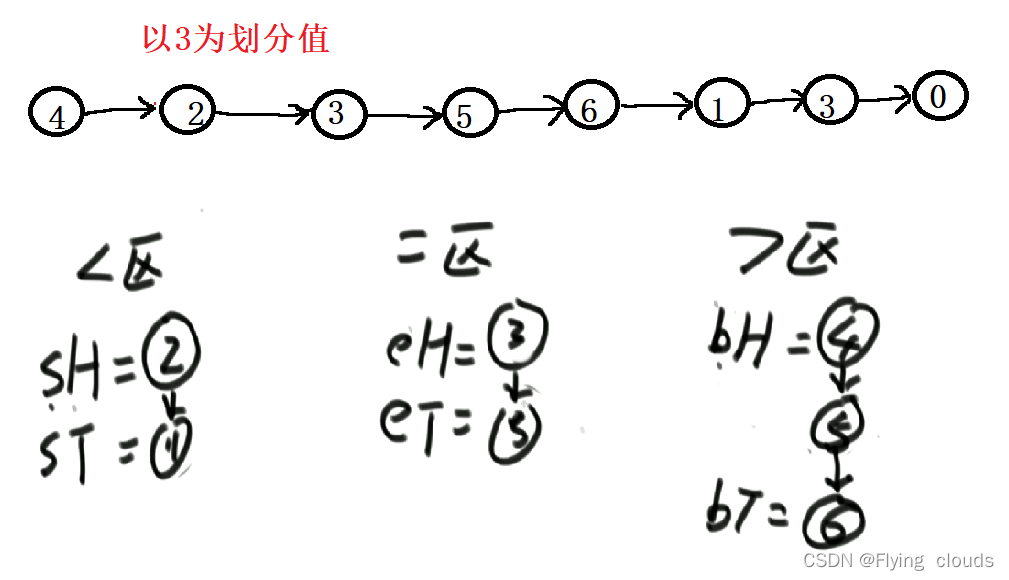
代码实现：

class SmallerEqualBigger
{
public:
	Node* listPartition2(Node* head, int pivot) 
	{
		Node* sH = nullptr; // small head
		Node* sT = nullptr; // small tail
		Node* eH = nullptr; // equal head
		Node* eT = nullptr; // equal tail
		Node* mH = nullptr; // big head
		Node* mT = nullptr; // big tail
		Node* next = nullptr; // save next node
		// every node distributed to three lists
		while (head != nullptr)
		{
			next = head->next;
			head->next = nullptr;
			if (head->value < pivot) 
			{
				if (sH == nullptr) 
				{
					sH = head;
					sT = head;
				}
				else 
				{
					sT->next = head;
					sT = head;
				}
			}
			else if (head->value == pivot) 
			{
				if (eH == nullptr) 
				{
					eH = head;
					eT = head;
				}
				else {
					eT->next = head;
					eT = head;
				}
			}
			else {
				if (mH == nullptr) 
				{
					mH = head;
					mT = head;
				}
				else {
					mT->next = head;
					mT = head;
				}
			}
			head = next;
		}
		// 小于区域的尾巴，连等于区域的头，等于区域的尾巴连大于区域的头
		if (sT != nullptr) 
		{ // 如果有小于区域
			sT->next = eH;
			eT = eT == nullptr ? sT : eT; // 下一步，谁去连大于区域的头，谁就变成eT
		}
		// 下一步，一定是需要用eT 去接 大于区域的头
		// 有等于区域，eT -> 等于区域的尾结点
		// 无等于区域，eT -> 小于区域的尾结点
		// eT 尽量不为空的尾巴节点
		if (eT != nullptr) 
		{ // 如果小于区域和等于区域，不是都没有
			eT->next = mH;
		}
		//return sH != nullptr ? sH : (eH != nullptr ? eH : mH);
		return sH;
	}
public:
	void printList(Node* node)
	{
		cout<<"Linked List: ";
		while (node != nullptr) 
		{
			cout<<node->value <<" ";
			node = node->next;
		}
		cout << endl;
	}

题型四、找到两条链表的第一个相交节点

这个题和约瑟夫环问题并称链表的两大噩梦

1、先找到两个链表的入环节点

1.利用set直接就能找到入环节点

 

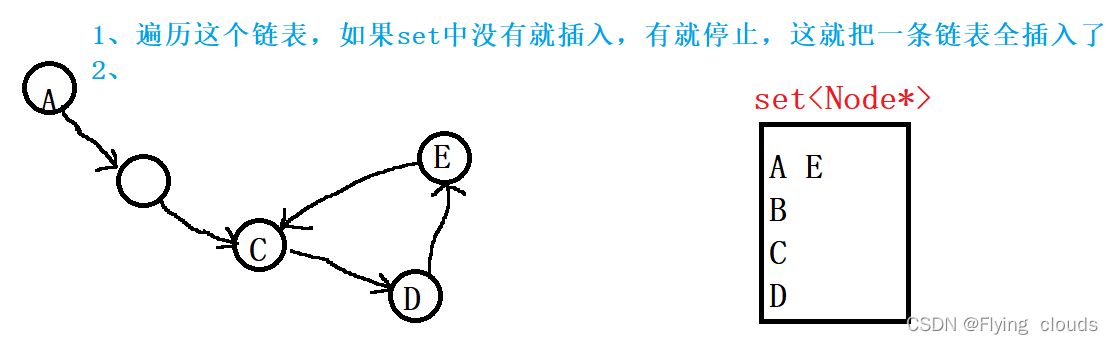
2.利用快慢指针

写一个函数实现这个功能

// 找到链表第一个入环节点，如果无环，返回nullptr
Node* GetLoopNode(Node* head)
{
	if (head == nullptr || head->next == nullptr || head->next->next == nullptr)
	{
		return nullptr;
	}
	// 快慢指针
	Node* slow = head->next; 
	Node* fast = head->next->next; 
	while (slow != fast)
	{
		if (fast->next == nullptr || fast->next->next == nullptr)
			return nullptr;//说明这个链表就没有环

		slow = slow->next;
		fast = fast->next->next;
	}
	//这时候是找到了第一个相遇的位置
	fast = head;
	while (slow != fast)//第二次是两个指针都一次走一步
	{
		slow = slow->next;
		fast = fast->next;
	}
	return fast;
}

2、接下来分情况讨论

我们已经有了能找到第一个入环节点的函数，head1 对应 loop1，head是loop2

2.1、loop1==nullptr && loop2==nullptr

 1.可以使用hash表去查第一个相交的部分

把一个链表全放入set中，然后第二个链表遍历去查在不在set中

2.也可以不用容器

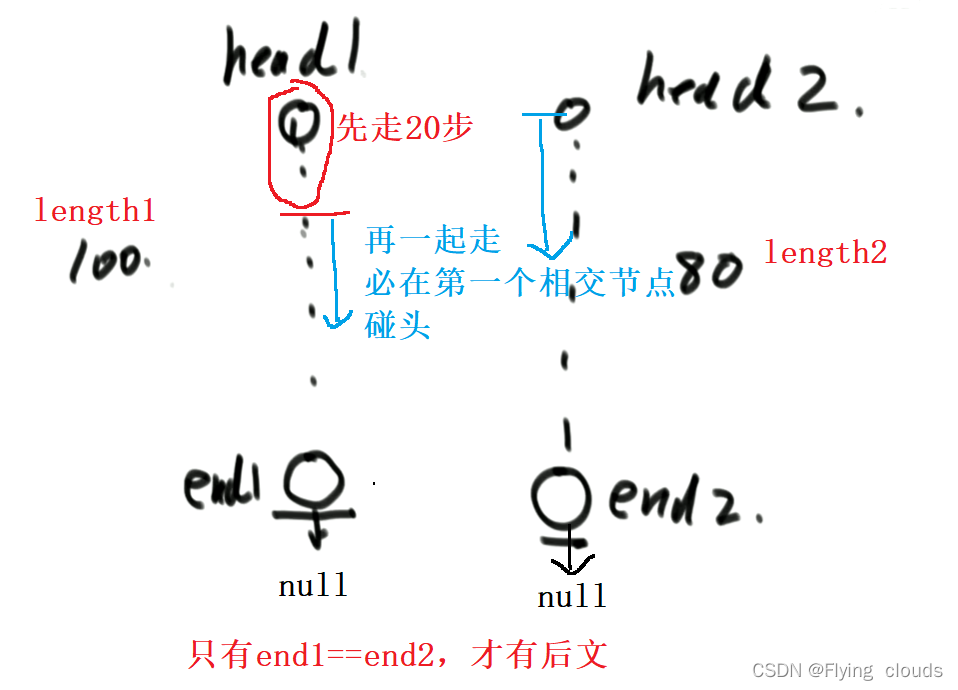
 代码：

// 如果两个链表都无环，返回第一个相交节点，如果不相交，返回nullptr
Node* NoLoop(Node* head1, Node* head2) {
	if (head1 == nullptr || head2 == nullptr) {
		return nullptr;
	}
	Node* cur1 = head1;
	Node* cur2 = head2;
	int n = 0;
	while (cur1->next != nullptr)
	{
		n++;
		cur1 = cur1->next;
	}
	while (cur2->next != nullptr)
	{
		n--;
		cur2 = cur2->next;
	}
	if (cur1 != cur2) {//说明没有相交的部分
		return nullptr;
	}
	if (n < 0)
	{
		cur1 = head2;
		cur2 = head1;
	}
	// n  :  链表1长度减去链表2长度的值
	cur1 = n > 0 ? head1 : head2; // 谁长，谁的头变成cur1
	cur2 = cur1 == head1 ? head2 : head1; // 谁短，谁的头变成cur2
	n = abs(n);
	while (n)
	{
		cur1 = cur1->next;
		n--;
	}
	while (cur1 != cur2)
	{
		cur1 = cur1->next;
		cur2 = cur2->next;
	}
	return cur1;
}

2.2、两条链表都有环（因为不可能一个有环一个没有环）

两个又换链表相交，一定是共用环的

 

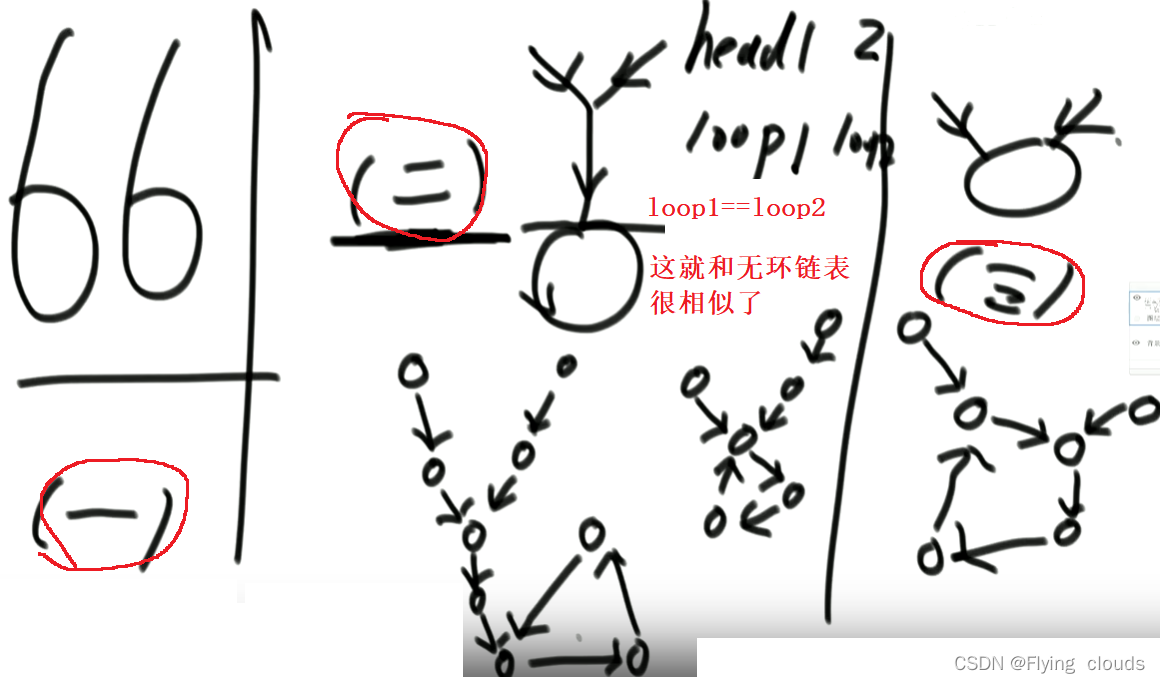
 情况（二）很好做，就和上面的无环链表的做法差不多了，

直接可以无视这个环，把两条链表的end看成是loop1就行了，然后做法就和上面的一样

（一）和 (二) 也可以区分开来

一个指针指向loop1->next,然后遍历一圈，看有没有loop2的存在，有就是（三）返回loop1和loop2都行，

没有就是（二）直接返回nullptr

// 两个有环链表，返回第一个相交节点，如果不想交返回nullptr
Node* BothLoop(Node* head1, Node* loop1, Node* head2, Node* loop2) {
	Node* cur1 = nullptr;
	Node* cur2 = nullptr;
	if (loop1 == loop2)
	{
		cur1 = head1;
		cur2 = head2;
		int n = 0;
		while (cur1->next != loop1)
		{
			n++;
			cur1 = cur1->next;
		}
		while (cur2->next != loop2)
		{
			n--;
			cur2 = cur2->next;
		}
		cur1 = n > 0 ? head1 : head2;//让cur1表示长的，cur2表示短的
		cur2 = cur1 == head1 ? head2 : head1;
		n = abs(n);
		while (n) {
			cur1 = cur1->next;
			n--;
		}
		while (cur1 != cur2) {
			cur1 = cur1->next;
			cur2 = cur2->next;
		}
		return cur1;
	}
	else
	{
		cur1 = cur1->next;
		while (cur1 != loop1)
		{
			if (cur1 == loop2)
				return loop1;
		}
		return nullptr;
	}
}

题型五、不给头节点，要求删一个给定的节点 ？

 1、小聪明法：借尸还魂

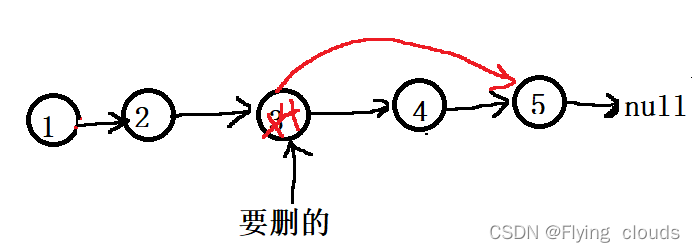
 但这个方法有很多问题

1、假如拷贝函数难以调用，就挂了

2、永远删不了最后一个节点

所以这是不行的，要删一个节点必须要给头节点

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/173582.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Allegro如何设置创建Pin Pair的快捷键操作指导

Allegro如何设置创建Pin Pair的快捷键操作指导

Allegro如何设置创建Pin Pair的快捷键操作指导 在做PCB设计的时候需要做一组信号的等长，需要使用到创建Pin Pair的功能，如下图，如果每个网络都右键去选择添加比较浪费时间，如下图 Allegro支持给创建一个Create Pin Pair的快捷键位 具体操作如下 打开规则管理器选择Tools
阅读更多...
单调栈与单调队列

单调栈与单调队列

单调栈与单调队列一、单调栈1.1 思路1.2 例题&#xff1a;单调栈二、单调队列2.1 思路2.2 例题&#xff1a;滑动窗口一、单调栈 1.1 思路 单调栈主要解决以下问题&#xff1a; 1️⃣ 寻找下一个更大元素 2️⃣ 寻找前一个更大元素 3️⃣ 寻找下一个更小元素 4️⃣ 寻找前一个…
阅读更多...
理性和感性 - 如何对待错误

理性和感性 - 如何对待错误

上次的博客&#xff0c; 我写了一些关于 软件开发中的理性和感性决定 的故事。 不论是感性还是理性&#xff0c;我们的目的就是要把软件交给用户去用&#xff0c; 在软件行业中有这样一句俗话&#xff1a; 当你把产品交给用户的时候&#xff0c;你的学习才刚刚开始。 当然每个团…
阅读更多...
【设计模式】结构型模式·桥接模式

【设计模式】结构型模式·桥接模式

学习汇总入口【23种设计模式】学习汇总(数万字讲解体系思维导图) 写作不易&#xff0c;如果您觉得写的不错&#xff0c;欢迎给博主来一波点赞、收藏~让博主更有动力吧&#xff01; 一.概述 将抽象与实现分离&#xff0c;使它们可以独立变化。用组合关系代替继承关系&#xff0c…
阅读更多...
华为数字化转型之道 结语 数字化转型的8个成功要素

华为数字化转型之道 结语 数字化转型的8个成功要素

结语 数字化转型的8个成功要素 华为开展数字化转型的过程中，积累了一些经验和教训，总结起来有如下成功要素。 1. 一把手担责 要做好数字化转型，企业家就要有战略决心、信心、耐心。数字化转型一定是企业“一把手工程”，需要企业家自上而下地推动并在企业内达成广泛共识。…
阅读更多...
免费开题报告|基于SpringBoot+Vue的校内跑腿平台

免费开题报告|基于SpringBoot+Vue的校内跑腿平台

作者主页&#xff1a;编程指南针 作者简介&#xff1a;Java领域优质创作者、CSDN博客专家 、掘金特邀作者、多年架构师设计经验、腾讯课堂常驻讲师 主要内容&#xff1a;Java项目、毕业设计、简历模板、学习资料、面试题库、技术互助 收藏点赞不迷路 关注作者有好处 文末获取源…
阅读更多...
Android 深入系统完全讲解（29）

Android 深入系统完全讲解（29）

MediaMuxer 封装器 MediaMuxer 最多仅支持一个视频 track 和一个音频 track&#xff0c;所以如果有多个音频 track 可以先 把它们混合成为一个音频 track 然后再使用 MediaMuxer 封装到 mp4 容器中。 MediaMuxer 支持输出格式为 MP4&#xff0c;webm 和 3gp. 默认我们就用 mp4.…
阅读更多...
产生聚类数据集sklearn.datasets.make_blobs()

产生聚类数据集sklearn.datasets.make_blobs()

【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 产生聚类数据集 sklearn.datasets.make_blobs() [太阳]选择题 以下python代码结果错误的一项是? import matplotlib.pyplot as plt from sklearn.datasets import make_blobs data,labelmak…
阅读更多...
统计-参数估计-假设检验-总结二

统计-参数估计-假设检验-总结二

统计-参数估计-假设检验-总结二参数估计—区间估计三大分布卡方分布(Gamma分布的特例)t分布F分布求估计区间假设检验参数检验拟合优度检验通往 统计-参数估计-假设检验-总结一参数估计—区间估计 以某一范围提供对参数θ\thetaθ的估计。寻找统计量θ1∗(x1,x2,...,xn)\theta…
阅读更多...
20230120英语学习

20230120英语学习

How Animals May Have Conquered Snowball Earth “雪球地球”时期&#xff0c;动物是如何存活的&#xff1f; Planet Earth used to be something like a cross between a deep freeze and a car crusher.During vast stretches of the planet’s history, everything from p…
阅读更多...
微信小程序开发尚学堂 介绍 项目结构 组件 喧嚷 事件 模板

微信小程序开发尚学堂 介绍 项目结构 组件 喧嚷 事件 模板

一、微信小程序介绍1. 微信小程序介绍微信小程序&#xff0c;简称小程序&#xff0c;是一种不需要下载安装即可使用的应用&#xff0c;它实现了应用”触手可及”的梦想&#xff0c;用户扫一扫或搜一下即可打开应用。说明&#xff1a;小程序是需要下载的&#xff0c;小程序的占用…
阅读更多...
概论_第6章_统计量及其抽样分布_知识结构

概论_第6章_统计量及其抽样分布_知识结构

先看知识结构图数量统计的特点是 背记的内容多&#xff0c; 与前面概率论 背记和计算的多 有很大区别。本文从统计量的概念讲起, 一. 统计量定义&#xff1a; 设 ...... 为取自某总体的样本&#xff0c; 若样本函数TT(, ... ) 中不含有任何未知参数&#xff0c; 则称T 为统计…
阅读更多...
力扣刷题记录——682. 棒球比赛、628. 三个数的最大乘积、693. 交替位二进制数

力扣刷题记录——682. 棒球比赛、628. 三个数的最大乘积、693. 交替位二进制数

本专栏主要记录力扣的刷题记录&#xff0c;备战蓝桥杯&#xff0c;供复盘和优化算法使用&#xff0c;也希望给大家带来帮助&#xff0c;博主是算法小白&#xff0c;希望各位大佬不要见笑&#xff0c;今天要分享的是——《力扣刷题记录——682. 棒球比赛、628. 三个数的最大乘积…
阅读更多...
企业实施RPA需考虑的20条建议

企业实施RPA需考虑的20条建议

如何提高效率又能降低成本&#xff0c;是企业发展所面临的重要挑战。在降本增效的路上&#xff0c;RPA&#xff08;机器人流程自动化&#xff09;以其特点与优势脱颖而出&#xff0c;迅速得到企业青睐。尽管如此&#xff0c;部署RPA也并非一蹴而就。仓促实施可能会给企业带来更…
阅读更多...
实时时钟实现

实时时钟实现

重要知识点 setInterval是一个实现定时调用的函数&#xff0c;可按照指定的周期&#xff08;以毫秒计&#xff09;来调用函数或计算表达式var sNownew Date()&#xff0c;Date 对象会自动把当前日期和时间保存为其初始值。 参数形式有以下&#xff15;种&#xff1a; new Dat…
阅读更多...
SpringBoot 接口幂等性实现的4种方案

SpringBoot 接口幂等性实现的4种方案

目录 什么是幂等性 什么是接口幂等性 为什么需要实现幂等性 引入幂等性后对系统的影响 Restful API 接口的幂等性 如何实现幂等性 方案一&#xff1a;数据库唯一主键 方案二&#xff1a;数据库乐观锁 方案三&#xff1a;防重 Token 令牌 方案四、下游传递唯一序列号 实…
阅读更多...
mysql连接查询

mysql连接查询

笛卡尔积现象&#xff1a; 注意&#xff1a; 效率更高的方法&#xff1a;
阅读更多...
Pr 计时器动画

Pr 计时器动画

​哈喽&#xff0c;各位小伙伴&#xff01;今天我们来学习一下如何制作数字滚动的计时器动画&#xff1f; 新建序列 新建一个1920*1080的序列&#xff0c;选择一张图片作为背景&#xff08;背景图出自不良人第5季&#xff0c;距离第6季开播还有41天&#xff09; 新建文字图层…
阅读更多...
5.算法通关面试 --- 递归and分治and贪心

5.算法通关面试 --- 递归and分治and贪心

50. Pow(x, n) https://leetcode.cn/problems/powx-n/
阅读更多...
【C语言从0到1之文件操作】（原理 画图 举例 不信教不会你 不要放收藏夹落灰 学起来好嘛）

【C语言从0到1之文件操作】（原理 画图 举例 不信教不会你 不要放收藏夹落灰 学起来好嘛）

&#x1f57a;作者&#xff1a;迷茫的启明星 &#x1f383;专栏&#xff1a;《数据库》《C语言从0到1专栏》《数据结构》《C语言杂谈》&#x1f3c7;分享喜欢的一句话&#xff1a;心如花木&#xff0c;向阳而生前言在我们的学习中&#xff0c;文件操作是被我们忽略&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023