统计-参数估计-假设检验-总结二
- 参数估计—区间估计
- 三大分布
- 卡方分布(Gamma分布的特例)
- t分布
- F分布
- 求估计区间
- 假设检验
- 参数检验
- 拟合优度检验
通往 统计-参数估计-假设检验-总结一
参数估计—区间估计
以某一范围提供对参数 θ \theta θ的估计。寻找统计量 θ 1 ∗ ( x 1 , x 2 , . . . , x n ) \theta_1^*(x_1,x_2,...,x_n) θ1∗(x1,x2,...,xn)和 θ 2 ∗ ( x 1 , x 2 , . . . , x n ) \theta_2^*(x_1,x_2,...,x_n) θ2∗(x1,x2,...,xn)满足 θ 1 ∗ < θ 2 ∗ \theta_1^*<\theta_2^* θ1∗<θ2∗;确定样本 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn之后,就将 θ \theta θ估计在区间 [ θ 1 ∗ ( x 1 , x 2 , . . . , x n ) , θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ] [\theta_1^*(x_1,x_2,...,x_n),\theta_2^*(x_1,x_2,...,x_n)] [θ1∗(x1,x2,...,xn),θ2∗(x1,x2,...,xn)]
满足上述要求的区间有很多,但具体估计的时候有优良性要求。
- θ \theta θ应尽可能大的在区间 [ θ 1 ∗ ( x 1 , x 2 , . . . , x n ) , θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ] [\theta_1^*(x_1,x_2,...,x_n),\theta_2^*(x_1,x_2,...,x_n)] [θ1∗(x1,x2,...,xn),θ2∗(x1,x2,...,xn)]内,也即: p ( θ 1 ∗ ( x 1 , x 2 , . . . , x n ) ≤ θ ≤ θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ) p(\theta_1^*(x_1,x_2,...,x_n)\leq\theta\leq\theta_2^*(x_1,x_2,...,x_n)) p(θ1∗(x1,x2,...,xn)≤θ≤θ2∗(x1,x2,...,xn))尽可能大
- 估计精度要尽可能高,即: θ 2 ∗ ( x 1 , x 2 , . . . , x n ) − θ 1 ∗ ( x 1 , x 2 , . . . , x n ) \theta_2^*(x_1,x_2,...,x_n)-\theta_1^*(x_1,x_2,...,x_n) θ2∗(x1,x2,...,xn)−θ1∗(x1,x2,...,xn)尽可能小。
实际上两者是冲突的,因此要引入置信区间的概念。
置信系数:给定一个很小的数
α
>
0
\alpha>0
α>0若对
θ
\theta
θ的任意值均有
p
(
θ
1
∗
(
x
1
,
x
2
,
.
.
.
,
x
n
)
≤
θ
≤
θ
2
∗
(
x
1
,
x
2
,
.
.
.
,
x
n
)
)
=
1
−
α
p(\theta_1^*(x_1,x_2,...,x_n)\leq\theta\leq\theta_2^*(x_1,x_2,...,x_n))=1-\alpha
p(θ1∗(x1,x2,...,xn)≤θ≤θ2∗(x1,x2,...,xn))=1−α称区间估计
[
θ
1
∗
,
θ
2
∗
]
[\theta_1^*,\theta_2^*]
[θ1∗,θ2∗]的置信系数为
1
−
α
1-\alpha
1−α
置信水平:如果 p ( θ 1 ∗ ( x 1 , x 2 , . . . , x n ) ≤ θ ≤ θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ) = 1 − α p(\theta_1^*(x_1,x_2,...,x_n)\leq\theta\leq\theta_2^*(x_1,x_2,...,x_n))=1-\alpha p(θ1∗(x1,x2,...,xn)≤θ≤θ2∗(x1,x2,...,xn))=1−α,而 β < 1 − α \beta<1-\alpha β<1−α;则 β \beta β均可称为 [ θ 1 ∗ , θ 2 ∗ ] [\theta_1^*,\theta_2^*] [θ1∗,θ2∗]的置信水平。
例如 1 − α = 0.95 1-\alpha=0.95 1−α=0.95,说明 θ \theta θ落在区间 [ θ 1 ∗ , θ 2 ∗ ] [\theta_1^*,\theta_2^*] [θ1∗,θ2∗]的概率等于0.95,置信水平为95%,或者比95%小的数,比如90%,当置信水平达到了95%,自然也达到了90%,置信水平越高,估计的区间也越大,如果区间是正无穷至负无穷,那置信水平也达到了100%,但此时是没有意义的。
三大分布
在学习三大分布之前,需要知道
Γ
\Gamma
Γ函数(Gamma函数),区分Gamma函数和Gamma分布。
Gamma分布的背景来自于对泊松分布的推导。
例如一个站台的呼叫数,它只与时间间隔有关,而与时间(刻)本身无关,设
ξ
(
t
)
\xi(t)
ξ(t)为
[
t
0
,
t
0
+
t
)
[t_0,t_0+t)
[t0,t0+t)内到达的呼叫数,则t时间间隔内到达k个呼叫数的概率
p
(
ξ
(
t
)
=
k
)
=
(
λ
t
)
k
k
!
e
−
λ
t
p(\xi(t)=k)=\frac{(\lambda t)^k}{k!}e^{-\lambda t}
p(ξ(t)=k)=k!(λt)ke−λt,服从泊松分布。记
τ
r
\tau_r
τr为第r个呼叫达到的时刻,根据泊松分布函数推导可以得到该自变量服从Gamma分布。
Gamma分布的密度函数:
g
(
r
,
λ
,
t
)
=
λ
r
t
r
−
1
e
−
λ
t
Γ
(
r
)
g(r,\lambda,t)=\frac{\lambda^rt^{r-1}e^{-\lambda t}}{\Gamma(r)}
g(r,λ,t)=Γ(r)λrtr−1e−λt
其中,r取整数时,
Γ
(
r
)
=
(
r
−
1
)
!
\Gamma(r)=(r-1)!
Γ(r)=(r−1)!
Γ
(
r
)
=
∫
0
∞
t
r
−
1
e
−
t
d
t
\Gamma(r)=\int_0^\infty t^{r-1}e^{-t}dt
Γ(r)=∫0∞tr−1e−tdt
为gamma函数(
λ
=
1
\lambda=1
λ=1, 对 t 进行了积分)
卡方分布(Gamma分布的特例)
自由度为n卡方分布: χ n 2 = Γ ( n 2 , 1 2 ) = ( 1 / 2 ) n / 2 y n / 2 e − 1 2 y π \chi_n^2=\Gamma(\frac{n}{2},\frac{1}{2})=\frac{(1/2)^{n/2}y^{n/2}e^{-\frac{1}{2}y}}{\sqrt{\pi}} χn2=Γ(2n,21)=π(1/2)n/2yn/2e−21y
他的期望为n,方差为2n
Gamma分布的特例,其中 r = n 2 r=\frac{n}{2} r=2n, λ = 1 2 \lambda=\frac{1}{2} λ=21
补充:若 ξ N ( μ , σ 2 ) \xi ~ N(\mu, \sigma^2) ξ N(μ,σ2),则 η = ξ 2 \eta=\xi^2 η=ξ2服从自由度为1的卡方分布。
t分布
f ( x ; n ) = Γ ( ( n + 1 ) / 2 ) n π Γ ( n / 2 ) ( 1 + x 2 n ) − ( n + 1 ) / 2 f(x;n)=\frac{\Gamma((n+1)/2)}{\sqrt{n\pi}\Gamma(n/2)}(1+\frac{x^2}{n})^{-(n+1)/2} f(x;n)=nπΓ(n/2)Γ((n+1)/2)(1+nx2)−(n+1)/2
他的期望为0,方差为 n / ( n − 2 ) n/(n-2) n/(n−2)
对应抽样分布:设总体服从正态分布, x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn为样本, X ˉ \bar X Xˉ记为样本均值, S S S记为方差,则:随机变量 n ( X ˉ − μ ) S \frac{\sqrt n(\bar X-\mu)}{S} Sn(Xˉ−μ)服从自由度为n的t分布
F分布
f ( x ; m , n ) = n n 2 n n 2 Γ ( n / 2 + m / 2 ) Γ ( n / 2 ) Γ ( n / 2 ) ( m + n t ) − m + n 2 t n / 2 − 1 f(x;m,n)=\frac{n^{\frac n2}n^{\frac n2}\Gamma{(n/2+m/2)}}{\Gamma{(n/2)}\Gamma{(n/2)}}(m+nt)^{-\frac{m+n}{2}}t^{n/2-1} f(x;m,n)=Γ(n/2)Γ(n/2)n2nn2nΓ(n/2+m/2)(m+nt)−2m+ntn/2−1
他的期望为 n / ( m − 2 ) ( m > 2 ) n/(m-2) (m>2) n/(m−2)(m>2) 方差为: 2 m 2 ( n + m − 2 ) n ( m − 2 ) 2 ( m − 4 ) \frac{2m^2(n+m-2)}{n(m-2)^2(m-4)} n(m−2)2(m−4)2m2(n+m−2)
对应抽样分布:两个总体X和Y,分别服从正态分布,所抽样本量分别为n和m。则随机变量 S X 2 S Y 2 / σ 1 2 σ 2 2 \frac{S_X^2}{S_Y^2}/\frac{\sigma_1^2}{\sigma_2^2} SY2SX2/σ22σ12服从自由度为n-1,m-1的F分布
求估计区间
求置信区间的方法:枢轴变量法。
-
寻找一个与要估计参数 g ( θ ) g(\theta) g(θ)有关的统计量 T = T ( x 1 , x 2 , . . . , x n ) T=T(x_1,x_2,...,x_n) T=T(x1,x2,...,xn),一般是其优良点估计量。
-
设法寻找包含统计量 T T T以及待估参数 g ( θ ) g(\theta) g(θ)的随机变量 S ( T , g ( θ ) ) S(T,g(\theta)) S(T,g(θ))。要求 S ( T , g ( θ ) ) S(T,g(\theta)) S(T,g(θ))的分布与 θ \theta θ无关, S S S为枢轴变量。这个变量是服从某种已知分布的,如正态分布、t分布或者F分布等等
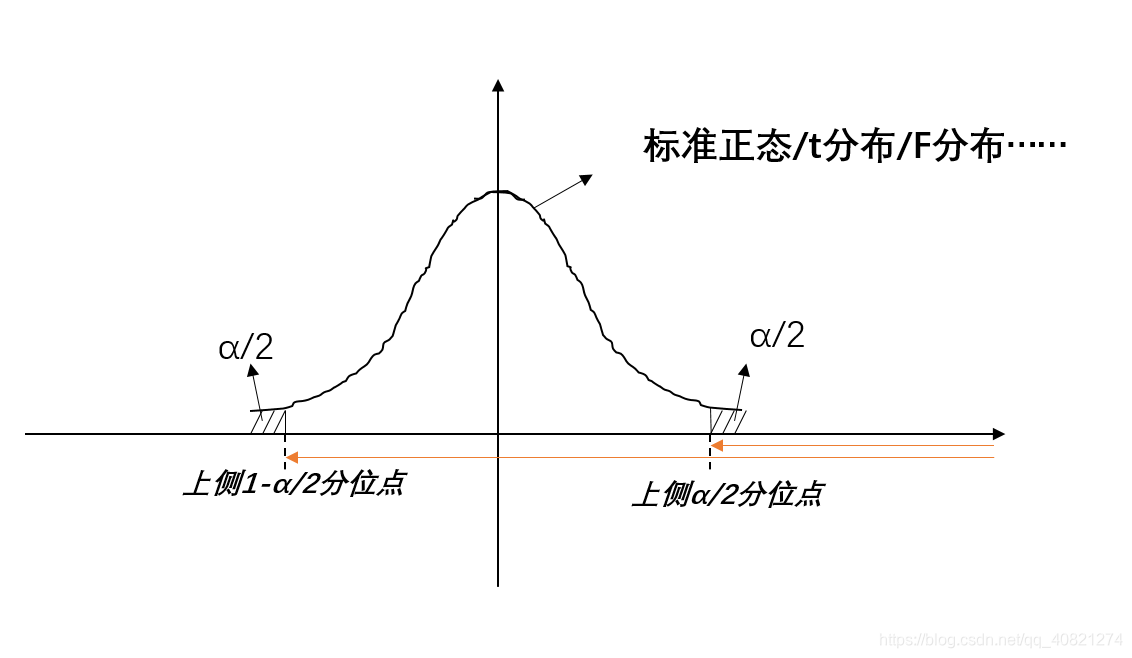
-
对于给定的 1 − α 1-\alpha 1−α,按照 p ( a ≤ S ( T , g ( θ ) ) ≤ b ) = 1 − α p(a\le S(T,g(\theta))\le b)=1-\alpha p(a≤S(T,g(θ))≤b)=1−α,求出a和b,这里求a和b实际上就是看分布的上下分位数
再由 a ≤ S ( T , g ( θ ) ) ≤ b a\le S(T,g(\theta))\le b a≤S(T,g(θ))≤b解出来 θ 1 ∗ ( T ) ≤ g ( θ ) ≤ θ 2 ∗ ( T ) \theta_1^*(T)\le g(\theta)\le \theta_2^*(T) θ1∗(T)≤g(θ)≤θ2∗(T)。则 [ θ 1 ∗ ( T ) , θ 2 ∗ ( T ) ] [\theta_1^*(T),\theta_2^*(T)] [θ1∗(T),θ2∗(T)]即为估计量的一个置信系数 1 − α 1-\alpha 1−α的区间估计。
常见的枢轴变量:
- 构造标准正态变量——某一变量服从正态分布(实际上自然界很多现象都服从正态分布),且其方差已知,对 μ \mu μ估计,他的优良估计连为 X ˉ \bar X Xˉ,可以构造随机变量 n ( X ˉ − μ ) σ \frac{\sqrt n(\bar X-\mu)}{\sigma} σn(Xˉ−μ),该变量服从标准正态分布,上下分位易求
- t分布变量——还是上例,如果方差未知的情况呢? n ( X ˉ − μ ) σ \frac{\sqrt n(\bar X-\mu)}{\sigma} σn(Xˉ−μ)的分布无从可知,因为分母含有未知变量。此时构造变量 n ( X ˉ − μ ) S \frac{\sqrt n(\bar X-\mu)}{S} Sn(Xˉ−μ),S为样本标准差;那这个变量服从 t n − 1 t_{n-1} tn−1分布,上下分位也易求得
- 卡方分布变量——举个非正态分布的例子。对于指数总体参数 1 / λ 1/\lambda 1/λ的区间估计,以 2 n λ X ˉ 2n\lambda\bar X 2nλXˉ作为枢轴变量。这个变量是服从 χ 2 n 2 \chi_{2n}^2 χ2n2的分布,也易求上下分位
- ……
区间估计达到预先设定的置信系数要求,就需要把关注点转移到精度要求之上,无穷大的估计区间,再准也是没有意义的。
以正态分布方差已知,估计均值的例子为例:
p ( θ 1 ∗ ( x 1 , x 2 , . . . , x n ) ≤ θ ≤ θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ) = 1 − α p(\theta_1^*(x_1,x_2,...,x_n)\leq\theta\leq\theta_2^*(x_1,x_2,...,x_n))=1-\alpha p(θ1∗(x1,x2,...,xn)≤θ≤θ2∗(x1,x2,...,xn))=1−α
p ( θ 1 ∗ ( x 1 , x 2 , . . . , x n ) ≤ n ( X ˉ − μ ) σ ≤ θ 2 ∗ ( x 1 , x 2 , . . . , x n ) ) = 1 − α p(\theta_1^*(x_1,x_2,...,x_n)\leq\frac{\sqrt n(\bar X-\mu)}{\sigma}\leq\theta_2^*(x_1,x_2,...,x_n))=1-\alpha p(θ1∗(x1,x2,...,xn)≤σn(Xˉ−μ)≤θ2∗(x1,x2,...,xn))=1−α
u 1 − α / 2 ≤ n ( X ˉ − μ ) σ ≤ u α / 2 u_{1-\alpha/2}\leq\frac{\sqrt n(\bar X-\mu)}{\sigma}\leq u_{\alpha/2} u1−α/2≤σn(Xˉ−μ)≤uα/2
σ u 1 − α / 2 n − X ˉ ≤ − μ ≤ σ u α / 2 n − X ˉ \frac{\sigma u_{1-\alpha/2}}{\sqrt n}-\bar X\leq-\mu\leq \frac{\sigma u_{\alpha/2}}{\sqrt n}-\bar X nσu1−α/2−Xˉ≤−μ≤nσuα/2−Xˉ
X ˉ − σ u α / 2 n ≤ μ ≤ X ˉ − σ u 1 − α / 2 n \bar X-\frac{\sigma u_{\alpha/2}}{\sqrt n}\leq\mu\leq \bar X-\frac{\sigma u_{1-\alpha/2}}{\sqrt n} Xˉ−nσuα/2≤μ≤Xˉ−nσu1−α/2
X
ˉ
−
σ
u
α
/
2
n
≤
μ
≤
X
ˉ
+
σ
u
α
/
2
n
\bar X-\frac{\sigma u_{\alpha/2}}{\sqrt n}\leq\mu\leq \bar X+\frac{\sigma u_{\alpha/2}}{\sqrt n}
Xˉ−nσuα/2≤μ≤Xˉ+nσuα/2
估计精度:
β
=
2
σ
u
α
/
2
n
\beta=\frac{2\sigma u_{\alpha/2}}{\sqrt n}
β=n2σuα/2
如果要求估计精度达到 β \beta β, 那相应样本容量n就要增大,大于多少也易求。
假设检验
参数检验
例如,在元件寿命服从指数分布的假定下,要通过对抽出若干个元件进行测试所得到的数据去判定“元件平均寿命不小于5000小时”是否成立问题。
原假设:
H
0
:
1
/
λ
≥
5000
H_0:1/\lambda\geq5000
H0:1/λ≥5000
对立假设:
H
1
:
1
/
λ
<
5000
H_1:1/\lambda<5000
H1:1/λ<5000
任何一个假设的检验都需要用到样本,如上例中服从指数分布,用样本去判断这个假设,首先要表达出平均,也就是对这个指数分布的均值进行估计。在这个检验中,只要样本的均值满足: X ˉ ≥ C \bar X\ge C Xˉ≥C(C为一个适当的数),就可以接受原假设.
则,能让原假设被接受的样本符合:
A
=
{
(
x
1
,
x
2
,
.
.
.
,
x
n
)
:
x
1
+
x
2
+
.
.
.
+
x
n
≥
n
C
}
A=\{(x_1,x_2,...,x_n):x_1+x_2+...+x_n\ge nC\}
A={(x1,x2,...,xn):x1+x2+...+xn≥nC}
这是一个样本集,也称 接受域;
同样,A的互补集为 拒绝域
给定的常数C是临界值,但无论给出什么临界值,都避免不了犯错误。(1)在原假设为真情况下,样本落在了拒绝域内,拒绝了原假设,出现第一类错误:弃真错误。(2)原假设非真,但样本落在了接受域内,从而接受原假设,出现第二类错误:取伪错误。由于样本的随机性,错误总是不可避免,只能尽可能降低犯错概率。
对于上例中,原假设被否定概率用
β
ϕ
(
λ
)
\beta_\phi(\lambda)
βϕ(λ)表示:
β
ϕ
(
λ
)
=
P
λ
(
X
ˉ
<
C
)
\beta_\phi(\lambda)=P_\lambda(\bar X<C)
βϕ(λ)=Pλ(Xˉ<C)
表示的是样本落在拒绝域内的概率。
上例中,由于
2
n
λ
X
ˉ
2n\lambda\bar X
2nλXˉ~
χ
2
n
2
\chi_{2n}^2
χ2n2,则有:
β
ϕ
(
λ
)
=
P
λ
(
X
ˉ
<
C
)
=
K
2
n
(
2
n
λ
C
)
\beta_\phi(\lambda)=P_\lambda(\bar X<C)=K_{2n}(2n\lambda C)
βϕ(λ)=Pλ(Xˉ<C)=K2n(2nλC)
可见,这个概率(样本落在拒绝域,也即均值小于5000小时)随 λ \lambda λ增大而增加, λ \lambda λ越大, 1 / λ 1/\lambda 1/λ越小,越小于5000小时,样本落在小于5000小时的概率就越大。作为一个合理的假设, λ \lambda λ越大,就应该用更大的概率否定原假设。
功效函数 是假设检验的重要概念:
β
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
=
P
θ
1
,
θ
2
,
.
.
.
,
θ
k
(
d
e
n
y
−
H
0
)
\beta_\phi(\theta_1,\theta_2,...,\theta_k)=P_{\theta_1,\theta_2,...,\theta_k}(deny-H_0)
βϕ(θ1,θ2,...,θk)=Pθ1,θ2,...,θk(deny−H0)
功效函数是未知参数的函数。当
θ
1
,
θ
2
,
.
.
.
,
θ
k
\theta_1,\theta_2,...,\theta_k
θ1,θ2,...,θk属于对立假设时,我们希望
β
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
\beta_\phi(\theta_1,\theta_2,...,\theta_k)
βϕ(θ1,θ2,...,θk)尽可能大(拒绝原假设的概率尽可能大)
发生两类错误的概率:
(1)原假设正确但被否了。用
α
1
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
\alpha_{1\phi}(\theta_1,\theta_2,...,\theta_k)
α1ϕ(θ1,θ2,...,θk)表示。
如果
θ
1
,
θ
2
,
.
.
.
,
θ
k
∈
H
0
\theta_1,\theta_2,...,\theta_k\in H_0
θ1,θ2,...,θk∈H0
α
1
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
=
β
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
\alpha_{1\phi}(\theta_1,\theta_2,...,\theta_k)=\beta_\phi(\theta_1,\theta_2,...,\theta_k)
α1ϕ(θ1,θ2,...,θk)=βϕ(θ1,θ2,...,θk)
如果
θ
1
,
θ
2
,
.
.
.
,
θ
k
∉
H
0
\theta_1,\theta_2,...,\theta_k\notin H_0
θ1,θ2,...,θk∈/H0
α
1
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
=
0
\alpha_{1\phi}(\theta_1,\theta_2,...,\theta_k)=0
α1ϕ(θ1,θ2,...,θk)=0
(2)原假设错误,但被接受。用
α
2
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
\alpha_{2\phi}(\theta_1,\theta_2,...,\theta_k)
α2ϕ(θ1,θ2,...,θk)表示。
如果
θ
1
,
θ
2
,
.
.
.
,
θ
k
∈
H
0
\theta_1,\theta_2,...,\theta_k\in H_0
θ1,θ2,...,θk∈H0
α
2
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
=
0
\alpha_{2\phi}(\theta_1,\theta_2,...,\theta_k)=0
α2ϕ(θ1,θ2,...,θk)=0
如果
θ
1
,
θ
2
,
.
.
.
,
θ
k
∉
H
0
\theta_1,\theta_2,...,\theta_k\notin H_0
θ1,θ2,...,θk∈/H0
α
2
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
=
1
−
β
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
\alpha_{2\phi}(\theta_1,\theta_2,...,\theta_k)=1-\beta_\phi(\theta_1,\theta_2,...,\theta_k)
α2ϕ(θ1,θ2,...,θk)=1−βϕ(θ1,θ2,...,θk)
检验水平 :一个常数
α
\alpha
α(
0
≤
α
≤
1
0\le\alpha\le1
0≤α≤1),对任何的
θ
1
,
θ
2
,
.
.
.
,
θ
k
∈
H
0
\theta_1,\theta_2,...,\theta_k\in H_0
θ1,θ2,...,θk∈H0,都有
β
ϕ
(
θ
1
,
θ
2
,
.
.
.
,
θ
k
)
≤
α
\beta_\phi(\theta_1,\theta_2,...,\theta_k)\le\alpha
βϕ(θ1,θ2,...,θk)≤α,称该检验为原假设在水平
α
\alpha
α的检验。
原假设认为 θ 1 , θ 2 , . . . , θ k ∈ H 0 \theta_1,\theta_2,...,\theta_k\in H_0 θ1,θ2,...,θk∈H0,如果对任意的参数取值 θ 1 , θ 2 , . . . , θ k ∈ H 0 \theta_1,\theta_2,...,\theta_k\in H_0 θ1,θ2,...,θk∈H0,都能保证犯错误的概率小于某个数 α \alpha α,那我们接受它的意愿就更有说服力了, α \alpha α取得小,犯第一类错误的概率很小。也即原假设正确下,所有可能的样本组合,能拒绝原假设的概率很小。反过来看,如果样本的所有可能组合,拒绝原假设的概率很小,设定某一水平,如果概率小于这个水平,是可以认为原假设正确的。
重要的假设检验:
(1)正态均值检验
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x1,x2,...,xn为正态总体抽取的样本,讨论
θ
\theta
θ的假设检验问题:
H
0
:
θ
≥
θ
0
;
H
1
:
θ
<
θ
0
H_0:\theta\ge\theta_0;H_1:\theta<\theta_0
H0:θ≥θ0;H1:θ<θ0
σ
2
\sigma^2
σ2已知时
选择
X
ˉ
\bar X
Xˉ作为参数
θ
\theta
θ的估计量,设定检验
ϕ
\phi
ϕ:当
X
ˉ
≥
C
\bar X\ge C
Xˉ≥C时,接受原假设,当
X
ˉ
<
C
\bar X< C
Xˉ<C时,否定原假设。
要给定常数C使之具有水平
α
\alpha
α,按照功效函数定义,在此检验下拒绝原假设的概率为:
β
ϕ
(
θ
)
=
P
θ
(
X
ˉ
<
C
)
=
P
θ
(
n
(
X
ˉ
−
θ
)
σ
<
n
(
C
−
θ
)
σ
)
=
ϕ
(
n
(
C
−
θ
)
σ
)
=
α
\beta_\phi(\theta)=P_{\theta}(\bar X<C)=P_{\theta}(\frac{\sqrt n(\bar X-\theta)}{\sigma}<\frac{\sqrt n(C-\theta)}{\sigma})=\phi(\frac{\sqrt n(C-\theta)}{\sigma})=\alpha
βϕ(θ)=Pθ(Xˉ<C)=Pθ(σn(Xˉ−θ)<σn(C−θ))=ϕ(σn(C−θ))=α
如果要检验水平为
α
\alpha
α,即要
β
ϕ
(
θ
)
≤
α
\beta_\phi(\theta)\le\alpha
βϕ(θ)≤α,
仅需取:
n
(
C
−
θ
)
σ
=
u
1
−
α
=
−
u
α
\frac{\sqrt n(C-\theta)}{\sigma}=u_{1-\alpha}=-u_\alpha
σn(C−θ)=u1−α=−uα
可得:
C
=
θ
0
−
σ
u
α
/
n
C=\theta_0-\sigma u_\alpha/\sqrt n
C=θ0−σuα/n
将C带入功效函数:
β
ϕ
(
θ
)
=
ϕ
(
n
(
θ
0
−
θ
)
σ
−
u
α
)
\beta_\phi(\theta)=\phi(\frac{\sqrt n(\theta_0-\theta)}{\sigma}-u_\alpha)
βϕ(θ)=ϕ(σn(θ0−θ)−uα)
从上式知, β ϕ \beta_\phi βϕ与参数 θ \theta θ、水平 α \alpha α以及标准差 θ \theta θ均有关:
拟合优度检验
理论分布已知,对分布检验
对分布的假设:
H
0
H_0
H0:
p
(
X
=
a
i
)
=
p
i
p(X=a_i)=p_i
p(X=ai)=pi, i=1,2,…,k
从总体中抽出容量n的样本或进行n次观察,得到样本 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,根据样本检验 H 0 H_0 H0, n p i np_i npi为 a i a_i ai的理论样本数量,统计 a i a_i ai出现的次数为 v i v_i vi(实际统计的样本数量),为观察值。
显然,差异越小越乐于接受它。
皮尔逊的拟合优度
χ
2
\chi^2
χ2统计量:
Z = ∑ n p i − v i n p i Z=\sum\frac{np_i-v_i}{np_i} Z=∑npinpi−vi
假设成立,在样本量很大时, Z Z Z服从自由度 k − 1 k-1 k−1的 χ 2 \chi^2 χ2的分布。
拟合优度 对这个检验,计算得到一定水平下的临界值为
Z
0
Z_0
Z0,显然当统计量Z满足
Z
>
Z
0
Z>Z_0
Z>Z0时否定原假设。在原假设为真时,
P
(
Z
>
Z
0
)
P(Z>Z_0)
P(Z>Z0)的概率就是犯错误的概率。定义拟合优度:
P
(
Z
0
)
=
P
(
Z
>
Z
0
∣
H
0
)
=
1
−
K
k
−
1
(
Z
0
)
P(Z_0)=P(Z>Z_0|H_0)=1-K_{k-1}(Z_0)
P(Z0)=P(Z>Z0∣H0)=1−Kk−1(Z0)
拟合优度越大,
Z
0
Z_0
Z0越小,犯错误的概率越低,表示理论与实际符合的越好。
例 一家工厂早中晚三班,每班8小时,发生一些事故,早班6次,中班3次,晚班6次,怀疑事故发生与班次有关。
H
0
H_0
H0(事故与班次无关)
p
i
=
1
/
3
p_i=1/3
pi=1/3,i =1,2,3
试验15次,可计算拟合优度统计量:
Z
0
=
(
(
5
−
6
)
2
+
(
3
−
6
)
2
+
(
5
−
6
)
2
)
/
5
=
1.2
Z_0=((5-6)^2+(3-6)^2+(5-6)^2)/5=1.2
Z0=((5−6)2+(3−6)2+(5−6)2)/5=1.2
χ
2
(
1.2
)
=
0.451
\chi_{2}(1.2)=0.451
χ2(1.2)=0.451,拟合优度
p
(
Z
0
)
=
0.549
p(Z_0)=0.549
p(Z0)=0.549
在一定准则下考虑是否拒绝原假设。
理论分布未知
总体X只取有限个值,其概率:
p
(
X
=
a
i
)
=
p
i
(
θ
1
,
θ
2
,
.
.
.
,
θ
r
)
p(X=a_i)=p_i(\theta_1,\theta_2,...,\theta_r)
p(X=ai)=pi(θ1,θ2,...,θr),其中,
θ
1
,
θ
2
,
.
.
.
,
θ
r
\theta_1,\theta_2,...,\theta_r
θ1,θ2,...,θr为未知参数。
设对X进行n次观察,以
v
i
v_i
vi记为X出现的次数。
假设:
H
0
:
p
(
X
=
a
i
)
=
p
i
(
θ
1
,
θ
2
,
.
.
.
,
θ
r
)
H_0: p(X=a_i)=p_i(\theta_1,\theta_2,...,\theta_r)
H0:p(X=ai)=pi(θ1,θ2,...,θr),对参数
θ
1
,
θ
2
,
.
.
.
,
θ
r
\theta_1,\theta_2,...,\theta_r
θ1,θ2,...,θr的某一组值
θ
1
0
,
θ
2
0
,
.
.
.
,
θ
r
0
\theta_1^0,\theta_2^0,...,\theta_r^0
θ10,θ20,...,θr0成立。
- 首先,要确定参数 θ 1 , θ 2 , . . . , θ r \theta_1,\theta_2,...,\theta_r θ1,θ2,...,θr,确定参数后才能进行拟合优度的检验。这一步为参数估计部分,利用样本数据对参数进行估计:采用极大似然法。(离散分布极大似然估计公式) L = n ! v 1 ! ⋅ v 2 ! . . . ⋅ v k ! P 1 v 1 ⋅ P 2 v 2 ⋅ . . . ⋅ P k v k L=\frac{n!}{v_1!\cdot v_2!... \cdot v_k!}P_1^{v_1}\cdot P_2^{v_2}\cdot...\cdot P_k^{v_k} L=v1!⋅v2!...⋅vk!n!P1v1⋅P2v2⋅...⋅Pkvk 解方程求取极大似然估计值
- 以估计值为参数真值,计算理论概率。在一定条件下,若原假设成立,当样本很大时, Z Z Z统计量分布趋向于 χ k − 1 − r 2 \chi_{k-1-r}^2 χk−1−r2.
- 若以 Z 0 Z_0 Z0记为算出来的具体统计量,算出 Z 0 Z_0 Z0的拟合优度 Z 0 > χ k − 1 − r 2 ( α ) Z_0>\chi_{k-1-r}^2(\alpha) Z0>χk−1−r2(α)时,否定原假设
列联表检验统计量
记
u
i
u_i
ui=p(属性A在水平i);
v
j
v_j
vj=p(属性B在水平j);
p
i
j
p_{ij}
pij=p(属性A在水平i且 属性B在水平j)。假设:
H
0
H_0
H0:
p
i
j
=
u
i
v
j
p_{ij}=u_iv_j
pij=uivj, i=1,2,…a; j = 1,2,…,b.
根据极大似然法,求得
u
^
i
=
n
i
⋅
n
\hat u_i=\frac{n_{i\cdot}}{n}
u^i=nni⋅;
v
^
j
=
n
j
⋅
n
\hat v_j=\frac{n_{j\cdot}}{n}
v^j=nnj⋅
由此可得
p
^
i
j
=
n
i
⋅
n
j
⋅
n
2
\hat p_{ij}=\frac{n_{i\cdot}n_{j\cdot}}{n^2}
p^ij=n2ni⋅nj⋅
第(i,j)得理论值: n p i j = n i ⋅ n j ⋅ n np_{ij}=\frac{n_{i\cdot}n_{j\cdot}}{n} npij=nni⋅nj⋅
统计量 Z = ∑ i a ∑ 1 b ( n ⋅ n i j − n i ⋅ n j ⋅ ) 2 n ⋅ n i ⋅ n j ⋅ Z=\sum_i^a\sum_1^b\frac{(n\cdot n_{ij}-n_{i\cdot}n_{j\cdot})^2}{n\cdot n_{i\cdot}n_{j\cdot}} Z=∑ia∑1bn⋅ni⋅nj⋅(n⋅nij−ni⋅nj⋅)2
例文化水平与支出
纵轴A,123表示教育水平高中低;横轴B,12表示支出水平高低。
| 1 | 2 | 3 | sum | |
|---|---|---|---|---|
| 1 | 63 | 37 | 60 | 160 |
| 2 | 16 | 17 | 8 | 41 |
| sum | 79 | 54 | 68 | 201 |
计算统计量 Z 0 Z_0 Z0为7.2078,拟合优度p=0.0207,过低,拒绝原假设:收入与文化消费无关。收入高者,文化指出偏低。










![[C/C++]指针,指针数组,数组指针,函数指针](https://img-blog.csdnimg.cn/ab6771adc5dc420883305bffed58d1e6.png)



