题目：122. 买卖股票的最佳时机 II

Leetcode题目地址
题目描述：
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在同一天出售。

返回你能获得的最大利润。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

本题重难点

这道题之前用动态规划算法进行过详细讲解一文搞懂动态规划之122. 买卖股票的最佳时机 II问题，同时这道题还可以使用贪心算法解决！

本题首先要清楚两点：

只有一只股票！
当前只有买股票或者卖股票的操作
想获得利润至少要两天为一个交易单元。

贪心算法思路：这道题目可能我们只会想，选一个低的买入，再选个高的卖，再选一个低的买入…循环反复。

如果想到其实最终利润是可以分解的，那么本题就很容易了！

如何分解呢？

假如第0天买入，第3天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑！

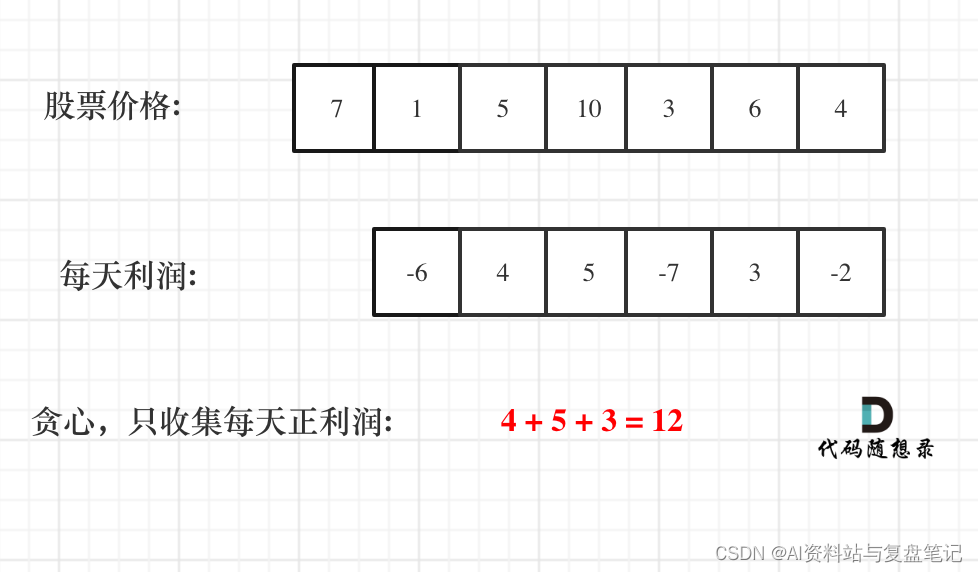
那么根据prices可以得到每天的利润序列：(prices[i] - prices[i - 1])…(prices[1] - prices[0])。

如图：

一些同学陷入：第一天怎么就没有利润呢，第一天到底算不算的困惑中。

第一天当然没有利润，至少要第二天才会有利润，所以利润的序列比股票序列少一天！

从图中可以发现，其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

那么只收集正利润就是贪心所贪的地方！

局部最优：收集每天的正利润，全局最优：求得最大利润。

局部最优可以推出全局最优，找不出反例，试一试贪心！

C++代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for(int i = 1; i < prices.size(); i++){
            res += max(prices[i] - prices[i - 1], 0);
        }
        return res;
    }
};