代码随想录–哈希表章节总结
1. LeetCode242 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
解题思路1: 利用HashMap。
- 首先循环第一个字符串,使用Map保存每一个字符出现的频率。
- 然后遍历第二个字符串,首先判断Map中是否包含这个字符,如果不包含,则直接返回false。否则将Map中当前字符出现的频率-1
- 然后再次遍历第一个字符串,这一次遍历实际上是遍历Map,如果发现Map中对应元素出现的频率不是0,那么返回false,否则循环结束返回true
public boolean isAnagram(String s, String t) {
// 如果两个字符串长度不同,则返回false
if (s.length() != t.length()) return false;
// 将其中一个字符串放入set集合
HashMap<Character, Integer> map = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (map.containsKey(c)) {
map.put(c, map.get(c) + 1);
} else {
map.put(c, 1);
}
}
// 遍历第二个字符串
for (int i = 0; i < t.length(); i++) {
char c = t.charAt(i);
if (!map.containsKey(c)) return false;
map.put(c, map.get(c) - 1);
}
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (map.get(c) > 0) return false;
}
return true;
}
解题思路2:思路实际上和思路1是一样的,只不过实现方式不再使用Map,而是使用数组
- 建立一个长度为26的数组,正好对应26个小写字母。数组的第一个位置代表a出现的次数,第二个位置代表b出现的位置,依此类推。
- 然后遍历第一个字符串,记录每一个元素出现的次数
- 然后遍历第二个字符串,发现出现的字符,就将出现次数-1
- 遍历整个数组,一旦发现数组中元素有不是0的,则返回false。循环结束,返回true。
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) return false;
int count[] = new int[26];
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i) - 'a']++;
}
for (int i = 0; i < t.length(); i++) {
count[t.charAt(i) - 'a']--;
}
for (int i = 0; i < count.length; i++) {
if (count[i] != 0) return false;
}
return true;
}
从运行时长可以看出,采用数组方式实现在时间上要快不少

2. LeetCode349 两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
解题思路1: 使用set集合,循环遍历将第一个数组中所有元素保存到set中,然后循环遍历第二个数组,将第二个数组中包含在set集合中的元素添加到返回set中。然后将返回set转化为int数组即可。
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set = new HashSet<>();
Set<Integer> res = new HashSet<>();
for (int i = 0; i < nums1.length; i++) {
if (!set.contains(nums1[i])) {
set.add(nums1[i]);
}
}
for (int i = 0; i < nums2.length; i++) {
if (set.contains(nums2[i])) {
res.add(nums2[i]);
}
}
return SetToInt(res);
}
private static int[] SetToInt(Set<Integer> allSet) {
// 先将set集合转为Integer型数组
Integer[] temp = allSet.toArray(new Integer[] {});//关键语句
// 再将Integer型数组转为int型数组
int[] intArray = new int[temp.length];
for (int i = 0; i < temp.length; i++) {
intArray[i] = temp[i].intValue();
}
return intArray;
}
解题思路2: 利用数组。使用数组来保存数组1中出现的元素。比如arr[1]就表示在数组1中元素1出现过。
- 遍历数组1,使用数组记录数组1中元素包含的数字
- 遍历数组2,判断数组2中是否包含数组1中的元素,如果包含保存到set中
- 将set转化为数组返回。
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set = new HashSet<>();
int[] hashArray = new int[1001];
// 遍历数组1,使用哈希数组记录数组1中包含的数字
for (int i = 0; i < nums1.length; i++) {
hashArray[nums1[i]] = 1;
}
// 遍历数组2
for (int i = 0; i < nums2.length; i++) {
if (hashArray[nums2[i]] == 1)
set.add(nums2[i]);
}
return set.stream().mapToInt(x -> x).toArray();
}
3. LeetCode202 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
解题思路: 对于满足快乐数条件的值,那么他最终会得到1,如果不满足,那么在经历n次循环后,sum的值会出现重复。因此我们利用set,判断是否值出现了重复,如果出现了重复,则不是快乐数,否则当循环结束后,返回true。
public boolean isHappy(int n) {
Set<Integer> set = new HashSet<>();
while (n != 1) {
if (set.contains(n)) return false;
set.add(n);
n = getRes(n);
}
return true;
}
private int getRes(int n) {
int res = 0;
while (n > 0) {
int temp = n % 10;
res += (temp * temp);
n = n / 10;
}
return res;
}
这个题另外值得学习的地方是如何取一个数字的每一个位对应的数字
private int getRes(int n) { int res = 0; while (n > 0) { int temp = n % 10; res += (temp * temp); n = n / 10; } return res; }
4. LeetCode1 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
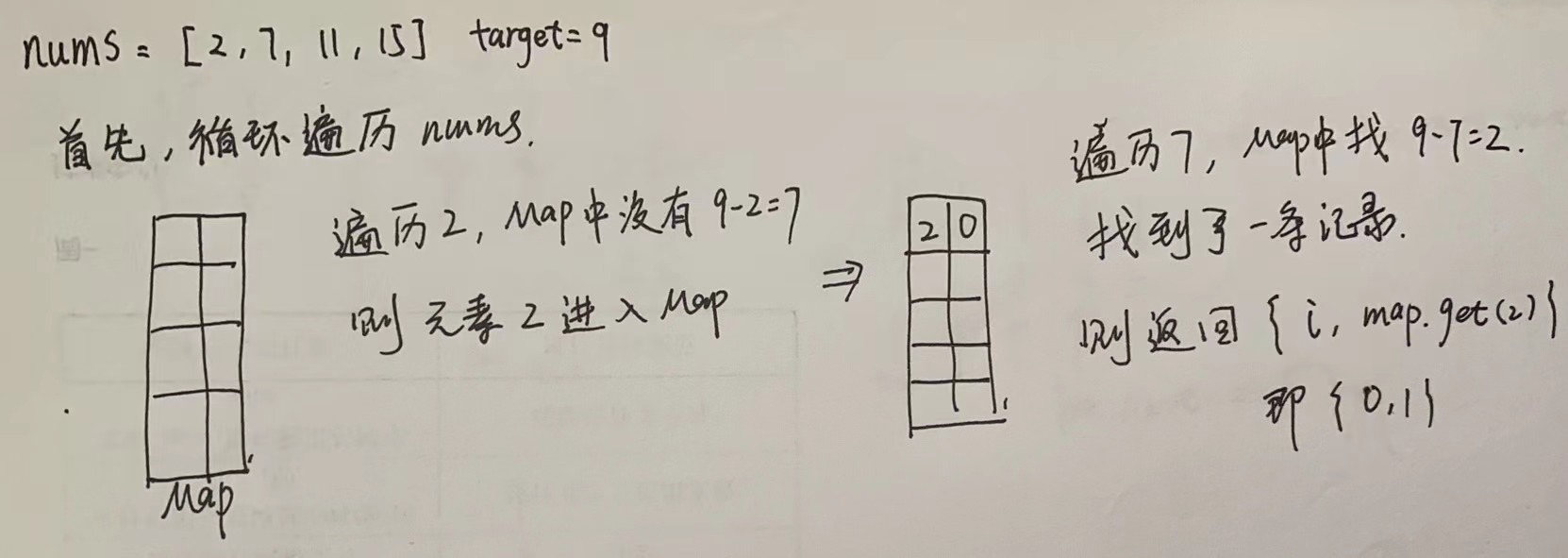
解题思路: 这道题可以利用Map来求解。
- 首先,循环遍历nums,每遍历一个元素,就到Map中判断有没有包含target-nums[i]的key,如果有那么就返回i,以及target-nums[i]为key的值。比如target = 9,当前取出的元素值为2,那么就去Map中查找是否之前遍历过7
- 否则,就将当前元素,以及当前元素的下标保存到Map中
- 一直遍历,知道遍历结束都没有返回的话,那么返回false
public int[] twoSum(int[] nums, int target) {
int[] a = new int[] {1, 2};
// 创建一个Map Key为数组中的元素,value为对应的下标
Map<Integer, Integer> map = new HashMap<>();
// 开始遍历数组
for (int i = 0; i < nums.length; i++) {
// 先判断之前是否遍历过符合要求的元素
// 比如target = 9,当前取出的元素值为2,那么就去Map中查找是否之前遍历过7
// 如果遍历过7,那么就找到了两个下标,分别是7对应的下标和当前的i
if (map.containsKey(target - nums[i])) {
// 如果存在,则直接返回
return new int[] {i, map.get(target - nums[i])};
}
// 否则 将当前元素加入map
map.put(nums[i], i);
}
return null;
}
因为是两个数求和,实际上就是先确定了一个数,然后另一个数肯定等于target-num, 然后再去找是否有满足target-num的数即可。
解题思路2:当然这个题也可以使用暴力法求解
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums.length; j++) {
if (i == j) continue;
if (nums[i] + nums[j] == target)
return new int[] {i, j};
}
}
return null;
}
对比一下两个方法的耗时,竟然差了100倍
5. LeetCode454 四数相加II
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < n
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
解题思路: 这个题如果我们使用暴力方法去做的话,时间复杂度高达 O ( n 4 ) O(n^4) O(n4),因此我们考虑其他方法。
- 首先我们可以将四个数组划分为两个数组,通过把nums1 nums2相加的这种方式。通过一个双重for循环,遍历nums1和nums2中两两相加的所有可能,并保存到Map中。Map的key为求和的值,value为等于这个值的组合的数量。
- 然后过一个双重for循环,遍历nums3和nums4中两两相加的所有可能,每遍历一个可能,就去判断在Map中是否存在0-(nums3[i]+nums4[j])的记录是否存在,如果存在则
count += map.get(0-(nums3[i]+nums4[j]))
Map中的key保存的是nums1,nums2两两相加所有可能的值,而value保存的是对应可能的值的所有组合方式个数
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
// 创建两个数组 分别用来保存nums1+nums2 nums3+nums4
// 数组长度相同
int[] sum = new int[nums1.length];
Map<Integer, Integer> map = new HashMap<>();
// 计算nums1 + nums2的所有可能和
for (int i = 0; i < nums1.length; i++) {
for (int j = 0; j < nums3.length; j++) {
int temp = nums1[i] + nums2[j];
if (map.containsKey(temp)) {
map.put(temp, map.get(temp) + 1);
} else {
map.put(temp, 1);
}
}
}
// 遍历nums3 + nums 4
Integer count = 0;
for (int i = 0; i < nums3.length; i++) {
for (int j = 0; j < nums4.length; j++) {
int temp = nums3[i] + nums4[j];
if (map.containsKey(-temp)) {
count += map.get(-temp);
}
}
}
return count;
}

为什么是两两组合呢?
是因为两两组合在遍历的时候,时间复杂度都是 O ( n 2 ) O(n^2) O(n2)的,所以一共的时间复杂度是 O ( 2 n 2 ) O(2n^2) O(2n2)
如果求第一个数组,存入Map,然后遍历nums2,nums3,nums4的可能性的话,那么时间复杂度为 O ( n + n 3 ) O(n+n^3) O(n+n3) 时间复杂度比较高
6.LeetCode303 赎金信
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。
如果可以,返回 true ;否则返回 false 。
magazine 中的每个字符只能在 ransomNote 中使用一次。
示例 1:
输入:ransomNote = "a", magazine = "b"
输出:false
示例 2:
输入:ransomNote = "aa", magazine = "ab"
输出:false
示例 3:
输入:ransomNote = "aa", magazine = "aab"
输出:true
解题思路: 这个题和之前的第一题思路是一样的。因为字符串中只有小写字母,因此采用数组的方式模拟哈希
- 首先遍magazine,然后计算出字符串中不同字符出现的次数
- 然后遍历ransomNote,在hash数组中找到匹配的就让出现的次数-1
- 遍历结束后,如果hash中的元素都大于等于0,返回true,否则返回false
public boolean canConstruct(String ransomNote, String magazine) {
// 遍历ransomNote,保存到hash数组中
// 数组中的值表示对应字符在ransomNote出现的次数
int[] hash = new int[26];
for (int i = 0; i < magazine.length(); i++) {
hash[magazine.charAt(i) - 'a']++;
}
for (int i = 0; i < ransomNote.length(); i++) {
hash[ransomNote.charAt(i) - 'a']--;
}
for (int i = 0; i < hash.length; i++) {
if (hash[i] < 0)
return false;
}
return true;
}
注意:一定要遍历magazine放入hash,而不是遍历ransomNote
举例 ransomNote = “a” magazine=“b”
- ransomNote放入hash,[1,0,…], magazine执行完–后,hash为[1,-1,0,…],看不出是不是符合
- magazine放入hash,[0,1,…], ransomNote执行完–后,hash为[-1,1,…],出现了-1,说明magazine中的字母已经不够用了,所以不满足。如果遍历完之后,hash中元素都是不小于0的,那么就满足。