前言

用不同的空间点模式分析方法，综合得出全国地名数据点的空间分布模式属于随机分布、均匀分布、聚集分布中的哪一种。

一、点模式分析

空间点模式分析是一种根据地理实体或事件的空间位置研究其分布模式的空间分析方法 。 空间点分布模式通常分为三种：随机分布、均匀分布和聚集分布。

二、点模式分析方法

空间点模式分析方法对应不同 的 空间点分布模式分为两 大类 一类是以聚集 性为基础的基于密度的方法，另一类是以分散性为基础的基于距离的方法 。

2.1基于密度的分析方法

基于密度的分析方法主要有两种：样方 计数法 和 核 密度分析法。

（1）样方计数法

样方分析 一般 使用随机分布模式作为理论上的标准分布， 将统计出的包含不同数量点的样方网格数量的频率分布与理论上的随机分布（如泊松分布）作比较通过显著性检验方法判断 点空间分布是否符合随机分布的假设。

这里需要指出的是：最优的正方形样方网格尺寸是根据研究区域的面积和分布于其中的点数量确定的，计算公式为 Q=2A/n ，其中Q 为样方面积， A 为研究区域面积， n为点数量。

泊松分布假设的是当研究区域内存在 n 个随机分布的点 时 ，一个样方中恰好有 1,2,3 …n个点落入其中的概率。

这里采用K-S显著性检验方法 ，假设观测频率分布与期望频率分布差异非常小，那么这种差异的出现存在偶然性，但如果差异大，偶然性就小 。

样方计数存在一定的限制，样方方法只能获得点在样方内的信息，不能获得样方内点之间等信息，即不能充分区分点的分布模式 。

（2）核密度分析法

密度分析是对离散地理事件进行内插生成连续表面的过程 ，从而可以找出点或者线比较集中的区域 。 核密度估计法认为地理事件在不同位置上发生概率不同 ，密集区域发生概率高，系数地区发生概率低 。

2.2基于距离的方法

这里采用两种基于距离的分析方法：最邻近距离法和K函数法。

（1）最邻近距离法

最邻近距离法使用最邻近的点之间的距离描述分布模式。它首先计算任意两点间的欧氏距离，比较得出最邻近距离， 并与随机分布模式的距离进行比较，若大于随机分布的距离，则点趋于均匀分布反之趋于聚集分布。在 ArcMap 中，用最邻近指数表征这一 指标，该指数为1 时 ，说明观测事件属于随机分布 当小于 1 时， 说明大量 事件点在空间上相互接近，属于空间聚集模式 当大于1 时空间 点是相互排斥地趋向于均匀分布 。

（2）K 函数（ L 函数）

最近邻距离法仅仅利用了最近邻距离，即空间分布的最小尺度，且结果依赖于空间点分布密度， K 函数 则在考虑事件 密度 的基础上 从 多个尺度来探讨空间分布状态，定义为某事件距离 d 内包含其他事件的理论数与 事件密度之比。

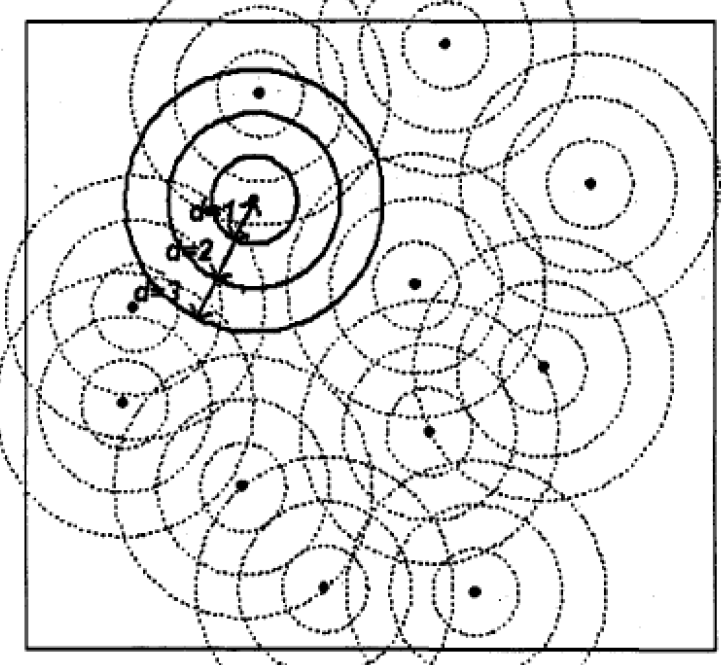
图1 K 函数计算方法示意图

对于一系列 d 值，这个过程不断重复所以得到：

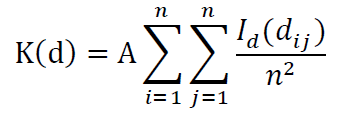
式中A 为 研究区域的面积， n 为事件个数 i=1,2,…,n j=1,2,…,n,(i≠ d 为空间距离尺度， 𝑑𝑖𝑗为 事件 i与事件 j之间的距离 𝑑𝑖𝑗≤𝑑时 𝐼𝑑(𝑑𝑖𝑗)为 1 𝑑𝑖𝑗>𝑑时 𝐼𝑑(𝑑𝑖𝑗)为 0 。K函数 的统计检验可通过 以 0 为 比较标准的规格化函数 L( d） 函数 来判断：

在随机分布的假设下， L(d)的 期望值为 0 。如果 L(d)<0 即 小于 随机分布下的期望值则认为空间点呈 均匀分布 若等于 0 则 认为 空间点 呈随机分布；若 大于 0 则认为空间点呈聚集分布。

三、实验数据

本次实验的数据包括 全国的地名数据点 （表格 数据 ）、 中国行政区划 （面 shp ）。首先将 全国 的地名数据点表格数据转为 点 shp 文件 points.shp 观察发现共有数据点699177个 ，分布在大陆 、港澳台及南海 地区。

四、实验过程

4.1 样方 计数法

（1） 生成样方

为了计算 最佳 样方大小， 需要赋予仅含 经纬度 信息 的图层 投影信息。将 points.shp 定义为

WGS84 坐标系转为阿尔伯特 (Albers) 投影 详细参数如下。

获得坐标信息 后， 最佳 样方大小 计算过程如下：

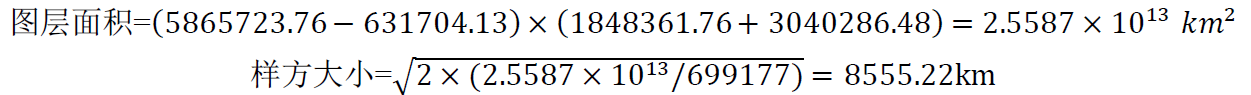
用【 Create Fishnet 】工具 生成样方，样方间距 设为 为 8555.22km 生成 样方面数据后， 设置样方 ID 号， 将属性表中的 Id 栏赋值为 FID+1 样方共 350064 格 。

（2）样方点数频率统计

统计每个样方内地名点的 数量，用【 spatial join 】工具连接样方图层和点数据 Target Features 设为点数据， Join Features 设为 样方，得到与每个 point 相交 Intersect 的 样方 ID 号 。表格 如下：

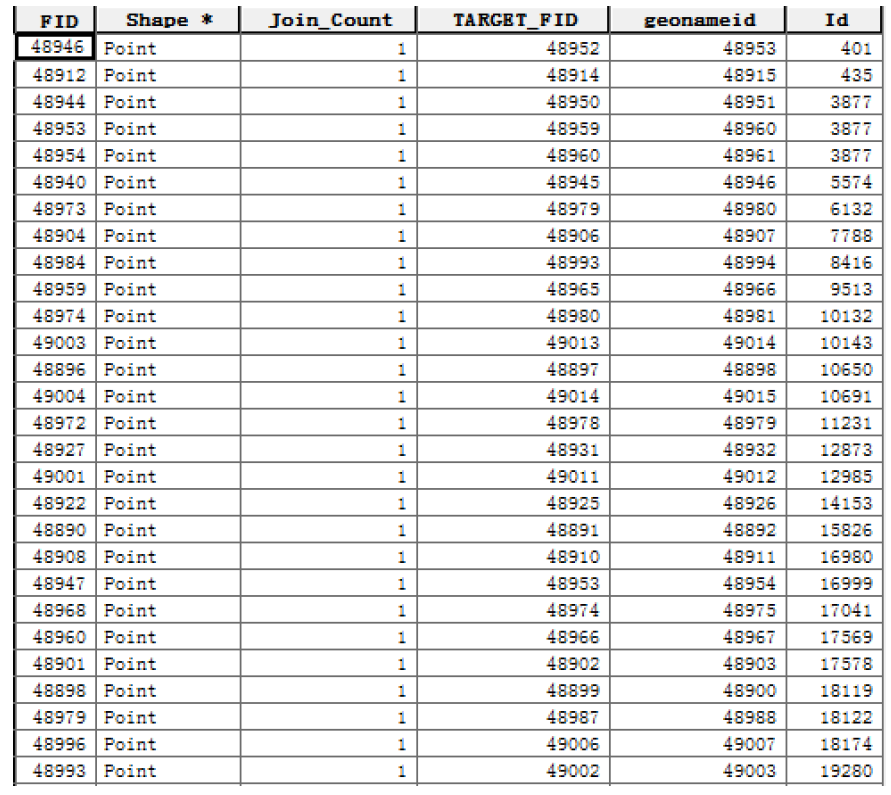
图2 地名点与样方空间连接结果

用summerize 工具统计 每个 样方 ID 号 对应 point 的数量， 即 求“Join_ 列 的总和， 得到每个样方内地名点 的数量得到专题图 （图 3 ）。从专题图 中可以看出，样方内地名点数量呈现出从东南沿海向西北内陆递减的趋势。

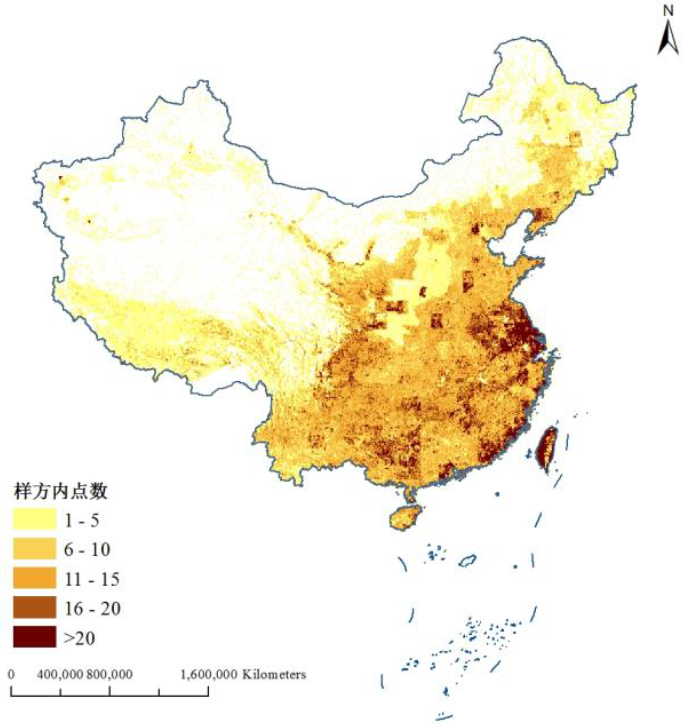
图3 全国地名点样方内点数分布图

统计不同每样方内点数出现 的频数， 并基于泊松分布计算期望分布频率表 。 首先计算每个样方内出现点的概率：

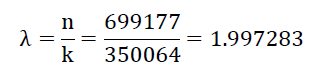
n表示点数， k 表示 样方数 。 在 Excel 内 用 泊松分布函数 POISSON.DIST(c,λ,I）计算期望频

率 c 样方内点数 1 。

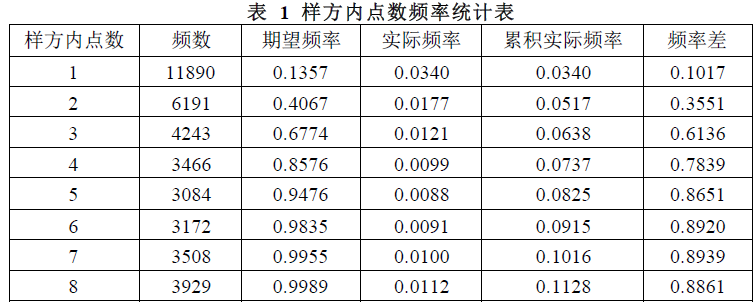
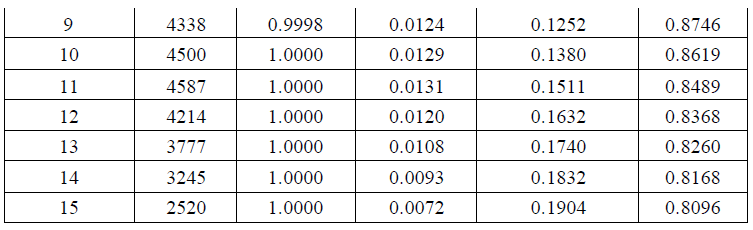
从表格中可见，期望 频率与累积 实际 频率 最大差 为 0.894 。

（3）分布模式判定

估计观测累计频率和期望累计频率表示为：

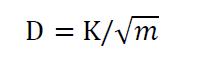
K为与显著性水平有关的常数， 当显著性水平为 0.05 时， K =1.36， m 为样方数， 由于 作为分

母的 m 极大， D 明显小于 表 1 中的 最大 频率差，说明 全国地名点数据不属于随机模式而属于聚集模式 或 分散模式之一 ，两个模式差异显著 。

4.2 核密度分析法

用【 Kernel Density 】工具 计算 点数据 的分布密度， 像元 大小设为 0.2 在不同的搜索半径下的点密度分布图 如下：

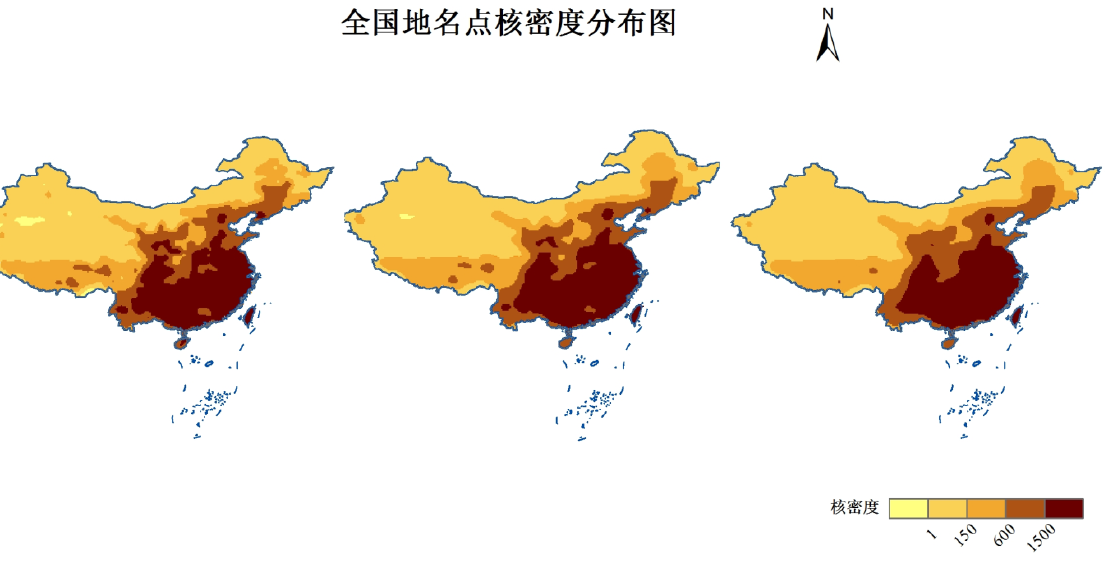
图4 全国地名点 核密度分布图 从左 到右搜索半径分别为 1, 1.5, 2)

由不同搜索半径的核密度分布图可以看出，大致以漠河腾冲一线为界， 东部地区核密度明显大于西部地区 ，即东部地区的地名点比西部更密集 。

4.3 最邻近距离法

选择【 Average Nearest Neighbor 】工具， 用欧氏距离进行最邻近距离法分析，测量每个要素与之最邻近要素之间的距离，并计算平均值，再比较平均距离与假定为随机分布距离的相似程度结果如下：

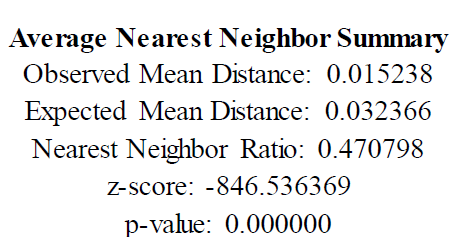
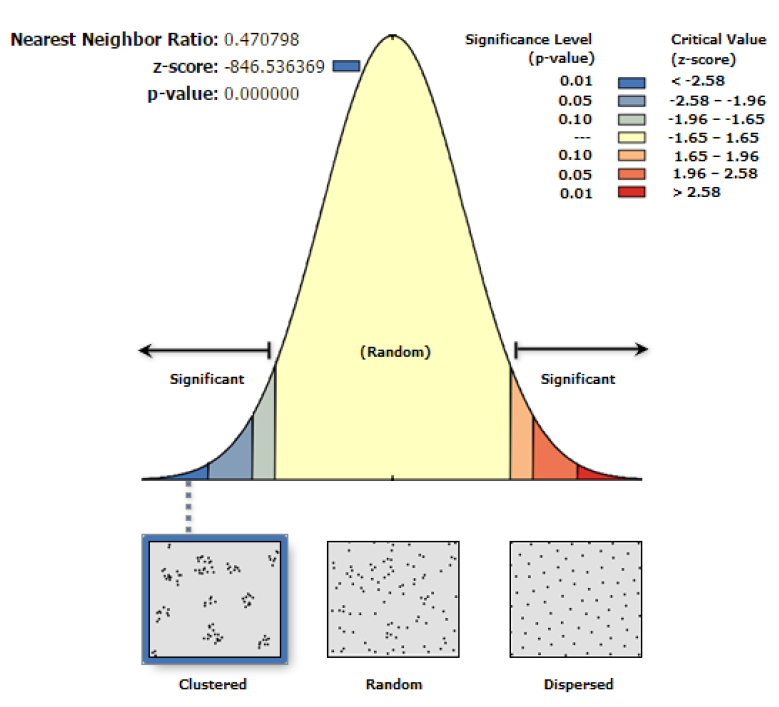
Observed Mean Distance是所研究的空间点与其最邻近点的距离的平均， Expected Mean Distance 是随机分布的空间点与其最邻近点的距离的平均，二者之比可以称为最邻近距离指数 。 z-score 和 p-value 表示的是最邻近分析结果的置信度， z-score 值为负且越小，则要素分布越趋向于聚类分布 。

本次分析中，最邻近指数为0.47 ，说明数据点是集聚的 ，且 z-score 为 846.54 ，p-value 约为 0 ，说明数据点呈聚集分布 ，且置信度约为 100% 。

5.4 K 函数

用CrimeStat 软件对 全国地名点的 空间分布进行 K 函数 分析，得到结果如下：

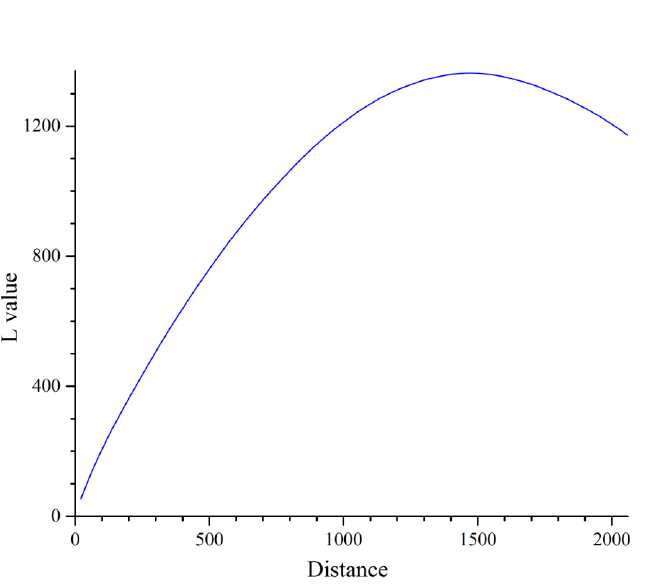
根据点空间分布的L 函数值，结果表明 全国地名点空间分布格局的聚集程度先增加后降低， 在 1460m （不精确，随投影变化而有差异）的尺度上聚集程度达到最大，即使随着点

间距离增大聚集程度有所降低，总体而言仍属于聚集分布 。

五、总结

本实验通过不同的 点模式 分析方法分析全国地名的分布模式。由样方计数法 可知 全国地名点数据不属于随机模式，而属于聚集模式或分散模式之一，两个模式差异显著。 而最邻近 距离法 进一步分析 得出全国地名点是 呈聚集分布 的， 聚集分布的置信度约为 100% 。 进一步看 核 密度分析 结果表明 地名点 大 致以漠河腾冲一线为界，东部地区核密度明显大于西部地区，即东部地区的地名点比西部更密集。 最后， 通过地名点分布的 L 函数可知 全国地名点空间分布格局的聚集程度先增加后降低，在 1460m （不精确，随投影变化而有差异）的尺度上聚集 程度 达到最大 即使 随着点间距离增大聚集程度有所降低，总体而言 仍 属于聚集分布。