函数

1 函数的概念

1.1 函数的定义

设𝑓是非空集A到B的关系, 如果对每个𝑥∈A, 都存在唯一的𝑦∈B, 使得<𝑥, 𝑦>∈𝑓, 则称关系𝑓为A到B的函数(Function), 也可称为映射(Mapping)或变换(Transformation), 记为𝑓: A→B。

• A为函数𝑓的定义域(Domain), 记为dom𝑓=A
• 𝑓(A)为函数𝑓的值域, 记为ran𝑓
• B称为函数𝑓的陪域(Codomain)

例如：
A={𝑥1, 𝑥2, 𝑥3}, B={𝑦1, 𝑦2}; f_1,f_2⊆A×B,
𝑓1={<𝑥1, 𝑦1>, <𝑥2, 𝑦2>, <𝑥3, 𝑦2>},
𝑓2={<𝑥1, 𝑦1>, <𝑥1, 𝑦2>};
则有𝑓1是函数, 𝑓2不是函数

1.2 函数的特点

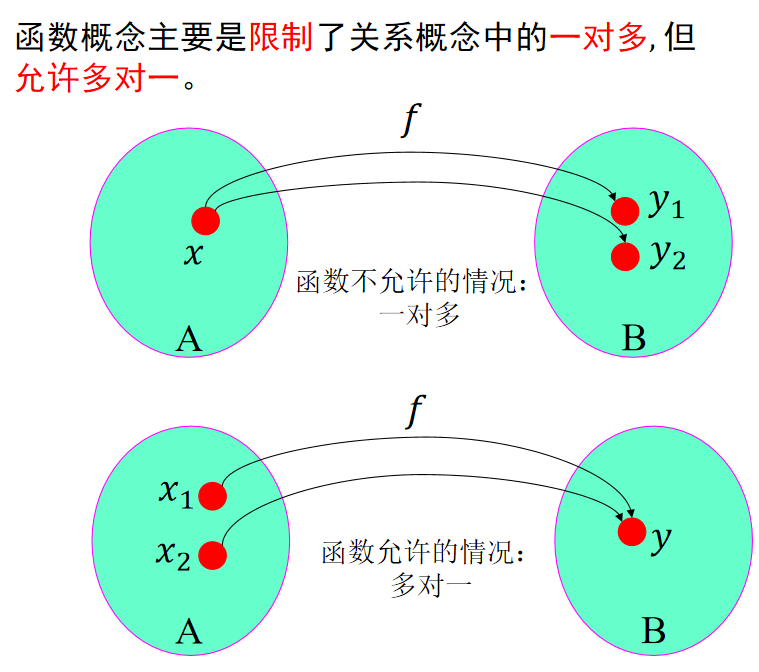
A到B的函数𝑓是从A到B的二元关系的子集, 且有以下特点:

• A的每一元素𝑎都必须是𝑓的有序对< 𝑎, 𝑏>之第一分量
• 若𝑓(𝑥)=𝑦, 则函数𝑓在𝑥处的值是唯一的, 即
  𝑓(𝑥)=𝑦 ⋀ 𝑓(𝑥)=𝑧$\Rightarrow$y=𝑧 (𝑥的像唯一)
• 允许一个像可有多个像源 (多对一)

例1 设A={1, 2, 3, 4}, B={𝑎, 𝑏, 𝑐, 𝑑}, 试判断下列关系哪些是函数。如果是函数, 请写出它的值域。
(1)𝑓1={<1, 𝑎>, <2, 𝑎>, < 3, 𝑑>, <4, 𝑐>}
(2)𝑓2={<1, 𝑎>, <2, 𝑎>, <2, 𝑑>, <4, 𝑐>}
(3)𝑓3={<1, 𝑎>, <2, 𝑏>, < 3, 𝑑>, <4, 𝑐>}
(4)𝑓4={<2, 𝑏>, < 3, 𝑑>, <4, 𝑐>}
解:
(1)𝑓1是函数。ran𝑓1={𝑎, 𝑐, 𝑑}；
(2)𝑓2不是函数；
(3)𝑓3是函数, ran𝑓3={𝑎, 𝑏, 𝑐, 𝑑}；
(4)𝑓4不是函数。

例2 设集合A={1，2，3}，B={a，b}，写出A到B的不同函数。
解：f0={<1，a>，<2，a>，< 3，a>}
f1={<1，a>，<2，a>，< 3，b>}
f2={<1，a>，<2，b>，< 3，a>}
f3={<1，a>，<2，b>，< 3，b>}
f4={<1，b>，<2，a>，< 3，a>}
f5={<1，b>，<2，a>，< 3，b>}
f6={<1，b>，<2，b>，< 3，a>}
f7={<1，b>，<2，b>，< 3，b>}
思考：有限集合A包含m个元素，B包含n个元素，从A到B的不同的函数有多少个？
答：幂集个数$2^m$、关系个数$2^{mn}$、函数个数$n^m$。

2 函数的性质

【定义】设𝑓: A→B
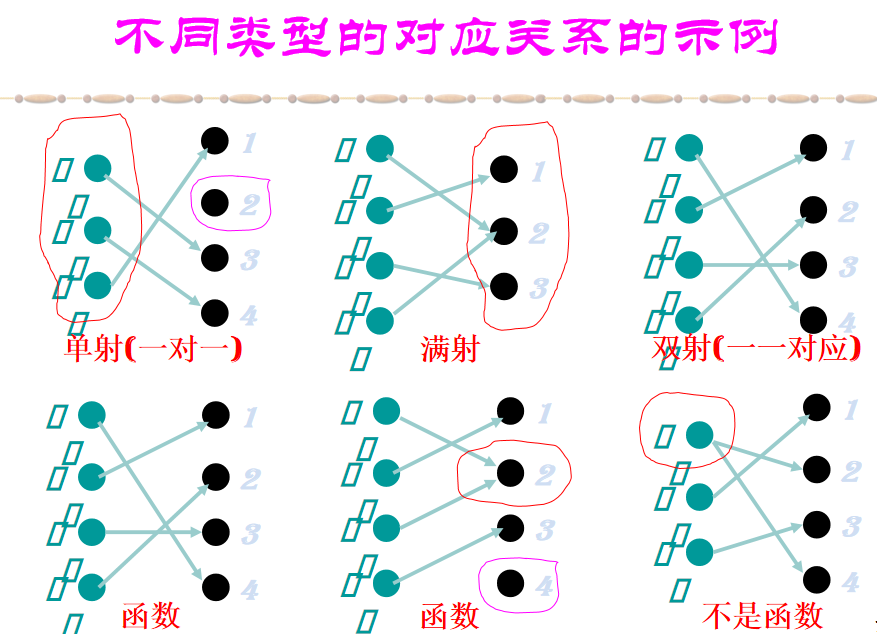
(1)若ran𝑓=B, 则称𝑓: A→B是满射(Onto, Surjection) 的；

• 陪域B“满”了
• 在函数𝑓的作用下, B中每个元素𝑏, 都至少是A中某元素𝑎的像
  $\forall b(b\in B\to \exists (a\in A\wedge f(a)=b))$
  (2)若𝑦ran𝑓 都存在唯一的𝑥A使得𝑓(𝑥)=𝑦, 则称𝑓: A→B是单(入)射(One-to-One, Injunction) 的；
• 定义域A“单”了
• A中不同的元素𝑎和𝑏, 其在B中像𝑓(𝑎)和𝑓(𝑏)也是不同的
  $\forall a\forall b(a\ne b\to f(a)\ne f(b))$
  或者 $\forall a\forall b(f(a)=f(b)\to a=b)$
  (3)若𝑓: A→B既是满射又是单射的, 则称𝑓: A→B是双射(One-to-One Correspondence, Bijection) 的
  B中的每个元素𝑏是且仅是A中某个元素𝑎的像
  
  例3 确定下列函数的类型。
  (1)设A={1, 2, 3, 4, 5}, B={𝑎, 𝑏, 𝑐, 𝑑}。
  𝑓: A→B定义为{<1, 𝑎>, <2, 𝑐>, < 3, 𝑏>, <4, 𝑎>, <5, 𝑑>}
  (2)设A={1, 2, 3}, B={𝑎, 𝑏, 𝑐, 𝑑}。
  𝑓: A→B定义为𝑓={<1, 𝑎>, <2, 𝑐>, < 3, 𝑏>}
  (3)设A={1, 2, 3}, B={1, 2, 3}。
  𝑓: A→B定义为𝑓={<1, 2>, <2, 3>, < 3, 1>}。
  解:
  (1)𝑓是满射函数；
  (2)𝑓是单射函数；
  (3)𝑓是双射函数。

3 函数的复合运算

函数是特殊的关系, 可以进行相应的运算。通过对函数的运算可以由已知函数得到新的函数。
定义 ：考虑𝑓: A→B, 𝑔: B→C是两个函数, 则𝑓与𝑔的复合运算𝑔∘𝑓={<𝑥, 𝑧>|𝑥∈A ⋀ 𝑧∈C ⋀ ($\exists y$)(𝑦∈B ⋀ 𝑥𝑓𝑦 ⋀ 𝑦𝑔𝑧)}是从A到C的函数记为𝑔∘𝑓: A→C，称为函数𝑓与𝑔的复合函数。
对$\forall x$∈A, 有(𝑔∘𝑓)(𝑥)=𝑔(𝑓(𝑥))。

例4 设
A={1, 2, 3, 4, 5}, B={𝑎, 𝑏, 𝑐, 𝑑}, C={1, 2, 3, 4, 5},
函数𝑓: A→B, 𝑓={<1, 𝑎>, <2, 𝑎>, < 3, 𝑑>, <4, 𝑐>, <5, 𝑏>}；
函数𝑔: B→C, 𝑔={<𝑎, 1>, <𝑏, 3>, <𝑐, 5>, <𝑑, 2>}。
求复合函数𝑔∘𝑓
解: 𝑔∘𝑓={<1, 1>, <2, 1>, < 3, 2>, <4, 5>, <5, 3>}
【说明】
复合函数𝑔∘𝑓就是复合关系𝑓∘𝑔。要注意的是为了方便, 当将其看作复合函数时, 在其表示记号中颠倒𝑓和𝑔的位置而写成𝑔∘𝑓。