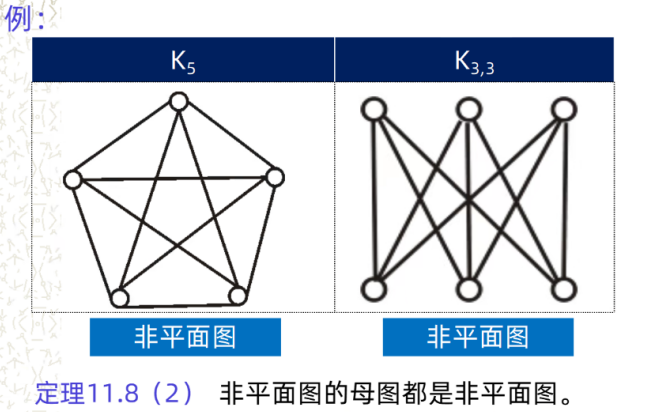
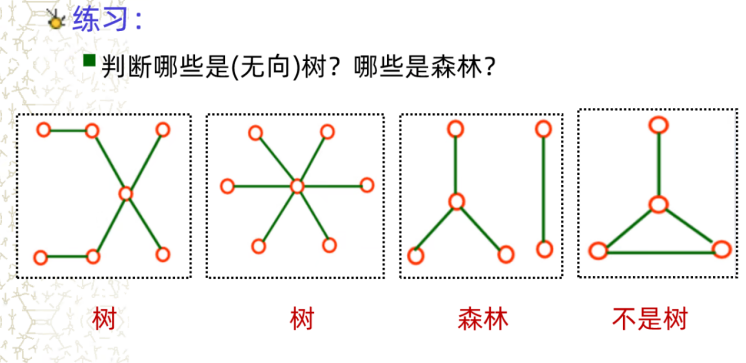
树

1 无向树及其性质

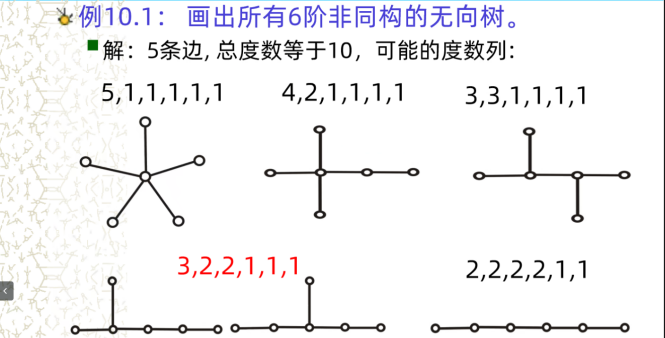
定义1：连通无回路的无向图称为无向树,简称树.每个连通分支都是树的无向图称为森林.平凡图称为平凡树.在无向树中,悬挂顶点称为树叶,度数大于或等于2的顶点称为分支点.

定义2 设G=<V,E>是n阶m条边的无向图，则下面各命题是等价的:
(1)G是树
(2)G中任意两个顶点之间存在惟一的路径.
(3)G中无回路且m=n-1.
(4)G是连通的且m=n-1.
(5)G是连通的且G中任何边均为桥.
(6)G中没有回路，但在任何两个不同的顶点之间加一条新边后所得图中有惟一的一个含新边的圈.

2 生成树与最小生成树

定义3 无向图G有生成树当且仅当G连通.
证：必要性显然.证充分性.若G中无回路，则G为自己的生成树．若G中含圈，任取一圈，随意地删除圈上的一条边;若仍有圈,再任取一个圈并删去这个圈上的一条边，重复进行,直到最后无圈为止.最后得到的图无圈（当然无回路）、连通且是G的生成子图，因而是G的生成树.这个产生生成树的方法称为破圈法.
推论G为n阶m条边的无向连通图，则m≥n-1.（因为连通需要n-1条边，4阶的无向图，边数至少是3条，3条边可以连通4个点）

定义4 设无向连通带权图G=<V,E,W>，T是G的一棵生成树，T的各边权之和称为T的权，记作w(T)．G的所有生成树中权最小的生成树称为G的最小生成树。

避圈法(Kruskal)：
输入:连通图G=<V,E,W>
输出:G的最小生成树T
1.将G中非环边按权从小到大排列:W(e1)≤W(e2≤…≤W(em).
2.令T<一{e1}, i<—2.
3.若ei,与T中的边不构成回路,则令T<一T∪{ei}
4.若|T|<n-1,则令i<一i+1,转3.

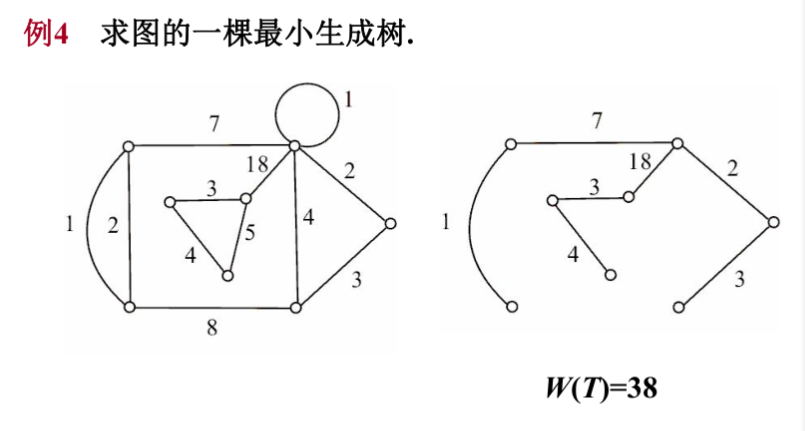
检查每一个圈，删掉权值最大的一条边，直到生成树中没有圈，权值最小，得出最小生成树，这就避圈法的原理。

3 根数及其应用

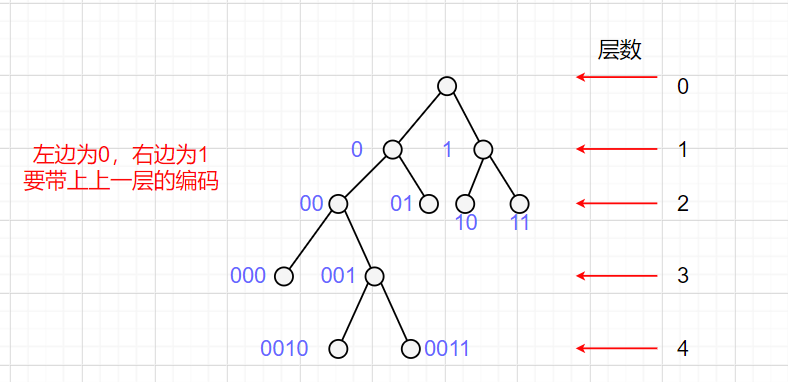
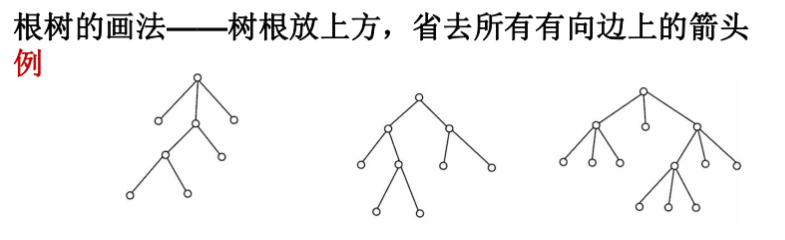
定义5 若有向图的基图是无向树,则称这个有向图为有向树.一个顶点的入度为0、其余顶点的入度为1的有向树称为根树．入度为0的顶点称为树根，入度为1出度为0的顶点称为树叶，入度为1出度不为0的顶点称为内点，内点和树根统称为分支点．从树根到顶点v的路径的长度(即,路径中的边数)称为v的层数.所有顶点的最大层数称为树高。

定义6 设T为一棵非平凡的根树, $\forall v_i,v_j\in V(T)$,若$v_i$,可达$v_j$,则称$v_i$为$v_j$的祖先, $v_j$为$v_i$的后代;若$v_i$邻接到$v_j$,则称$v_i$为$v_j$的父亲，$v_j$为$v_i$的儿子.若$v_j,v_k$的父亲相同,则称$v_j$与$v_k$是兄弟.

将根树T中层数相同的顶点都标定次序,称T为有序树.
根树的分类:
(1)若T的每个分支点至多有r个儿子，则称T为r叉树.
(2)若T的每个分支点都恰好有r个儿子,则称T为r叉正则树.
(3)若T是r叉正则树,且所有树叶的层数相同,则称T为r叉完全正则树.
有序的r叉树, r叉正则树,r叉完全正则树分别称作r叉有序树，r叉正则有序树，r叉完全正则有序树.
定义7
定义 设T为一棵根树, $\forall v\in$V(T),称v及其后代的导出子图$T_v$,为以v为根的根子树.
2叉正则有序树的每个分支点的两个儿子导出的根子树分别称为该分支点的左子树和右子树.
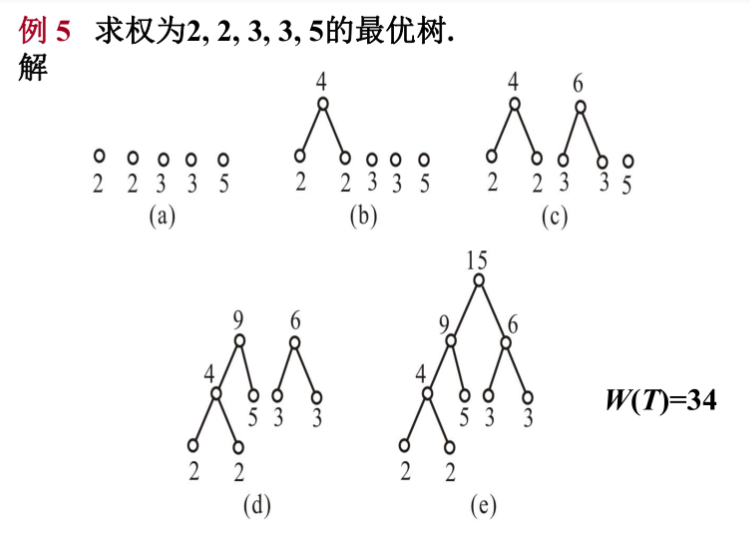
定义 设2叉树T有t片树叶$v_1,v_2,..v_t$,权分别为$w_1,w_2,\dots ,w_t$,称”${\sum }_{i=1}^n{w}_i{l}_i$为T的权,其中$l_i$是$v_i$的层数.在所有有t片树叶，带权$w_1,w_2,\dots ,w_t$的2叉树中,权最小的2叉树称为最优2叉树.

4 前缀码

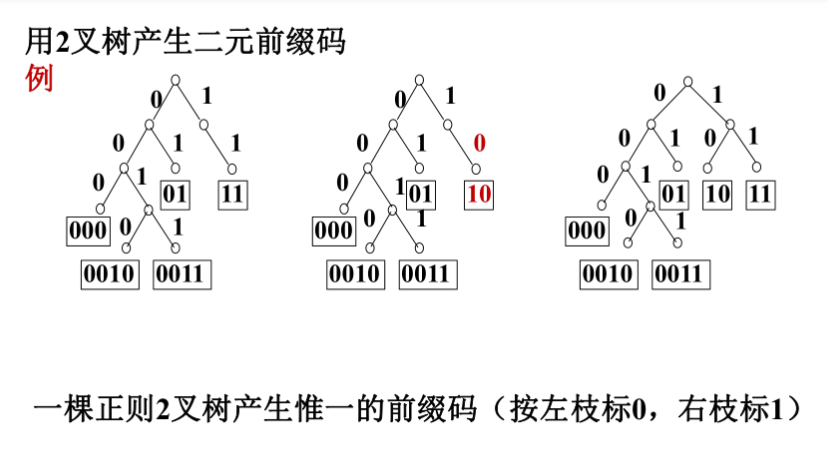
结论：从上到下随层数位数(0,1,2,3,4…),左边取0，右边取1
例如：