题目

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

限制：

1 <= s 的长度 <= 8

---

思路：递归+回溯+剪枝

问题转化：求字符串中n个字符的全排列 -> 构造成一颗n叉树，求一个n叉树有多少条路径。

这道题可以以任意顺序返回这个字符串数组，但里面不能有重复元素，需要去重：

①可以用hashSet去重，但不是一个好的方法，因为在全排列的过程其实就是在搜素n叉树的过程，用hashSet并没有起到一个剪枝的作用，考虑下一种方法。

②先将字符串转成一个字符数组arr，对数组进行排序，构建n叉树，递归+回溯来进行搜素，还需要剪枝：

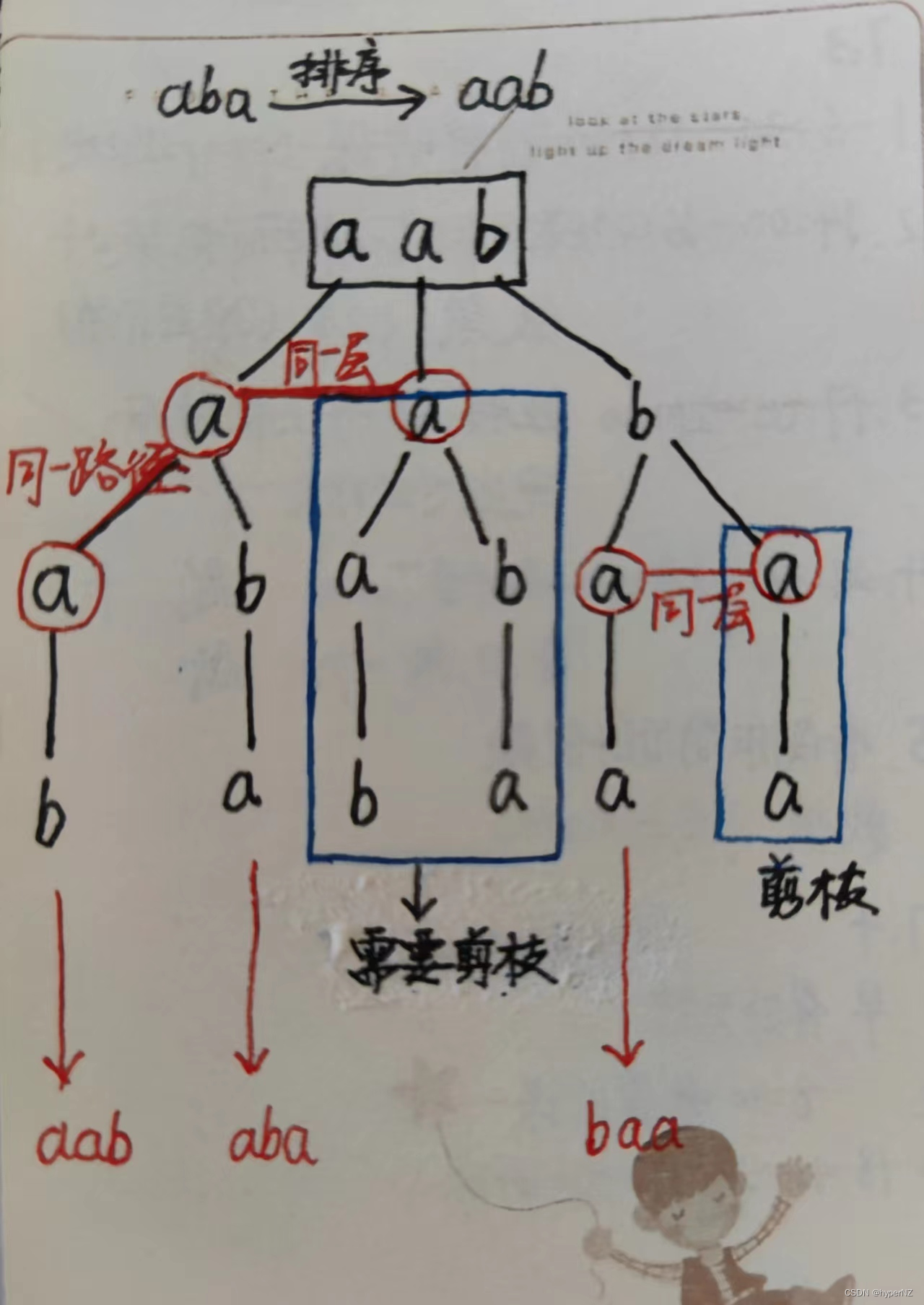
判断两个相同的元素值，是在相邻位置，且在同一层时才需要剪枝（不继续走递归了）。

用visited做标记方便后面判断是否访问过某个元素：false表示还没有被访问，true表示已经被访问过。

arr[i]==arr[i - 1]说明两个相同的元素值在相邻位置；

visited[i- 1] = false表示arr[i - 1]没有被访问过，则arr[i]与arr[i - 1]为同一层，需要剪枝，不走递归；

visited[i- 1] = true表示arr[i - 1]被访问过，则arr[i]与arr[i - 1]为同一路径，不需要剪枝，走递归，若visited[i] = false说明arr[i]没有被访问，将其visited状态置为true，并将其加入临时访问路径path集中，再递归搜索所有还没有被访问过的子树节点，搜索完之后需要回溯回去，从path集中删除arr[i]，并让visited[i] = false。

若能访问到第k个元素，k等于数组长度，说明是一条可行路径，将路径path记录到结果集res中。

例：

输入：s = "aba"
输出：["aab","aba","baa"]

---

代码

class Solution {
    List<Character> path; //记录临时访问过的路径
    List<String> res; //记录结果集
    boolean[] visited; //做标记方便后面判断是否访问过某个元素

    public String[] permutation(String s) {
        //初始化
        this.path = new ArrayList<>();
        this.res = new ArrayList<>();
        this.visited = new boolean[s.length()];

        //将字符串转换为字符数组
        char[]  arr = s.toCharArray();
        //对字符数组进行排序
        Arrays.sort(arr);
        dfs(arr, 0);

        //将结果集转换为字符串数组
        String[] ss = new String[res.size()];
        for(int i = 0; i < res.size(); i++) {
            ss[i] = res.get(i);
        }
        return ss;
    }

    /**
     * 深度搜索函数作用是对字符数组中的元素进行全排列并去重
     * @param arr
     * @param k
     */
    void dfs(char[] arr, int k) {
        //k表示访问到第几个元素
        if(arr.length == k) { //说明是一条可行路径
            res.add(listToString(path)); //记录到结果集中
            return;
        }

        //进行n叉树搜索,进行全排列（去重）
        for(int i = 0; i < arr.length; i++) {
            //剪枝：是相邻的元素且前一个元素没有被访问过，是在同一层
            //i > 0因为第一个不用剪枝
            if(i > 0 && arr[i] == arr[i- 1] && visited[i - 1] == false) {
                continue; //什么都不做
            }
            //第i个元素还没有被访问过，去进行递归访问
            if(visited[i] == false) {
                visited[i] = true;
                path.add(arr[i]);
                //递归搜索所有还没有被访问过的子树节点
                dfs(arr, k + 1);
                //搜索完之后需要回溯回去
                path.remove(path.size() - 1);
                visited[i] = false;
            }
        }
    }

    /**
     * 将list转换成String
     * @param list
     * @return
     */
    String listToString(List<Character> list) {
        StringBuilder b = new StringBuilder();
        for(int i = 0; i < list.size(); i++) {
            b.append(list.get(i));
        }
        return b.toString();
    }
}

时间复杂度：O(n*n!)

空间复杂度：O(n)