文章目录
- 62. 不同路径
- 题意
- 解法1 排列组合
- 解法2 动态规划
62. 不同路径
题意
- 一道数学题,排列组合/小学奥赛题。
- 动态规划不是一般来解决最值问题的吗,这道题为什么会想到dp?
解法1 排列组合
从左上角到右下角,一共要走m+n-2步,其中向右n-1步,向下m-1步,因此路径的总数,相当于从m+n-2中选择m-1个向下的步数,即排列组合。

- 但是,需要注意的是,题目只保证最后结果在
int型范围内,而实际上如果按下面的代码运行,即便中间运算已经用long long存储,还是会溢出,所以需要一边乘一边除(即便是一边乘一边除,中间过程也必须用long long,否则中间计算会超出int型可表示范围)。
class Solution {
public:
int uniquePaths(int m, int n) {
long long ans=1;
for(int i=n;i<=m+n-2;i++)
ans=ans*i; //会溢出
for(int i=1;i<m;i++)
ans/=i;
return ans;
}
};
// ac代码
class Solution {
public:
int uniquePaths(int m, int n) {
long long ans=1;
for(int i=n,j=1;i<=m+n-2;i++,j++)
ans=ans*i/j;
return ans;
}
};
解法2 动态规划
dp[i][j]表示走到 (i,j) 这个位置有几种走法。dp[i][j]=dp[i-1][j]+dp[i][j-1]。- 注意
dp[0][0]和边界情况(i-1和j-1)处理(也可以将dp[0,:]和dp[:,0]全置1)。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int> > dp(m,vector<int>(n,0));
dp[0][0]=1;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(dp[i][j]==0) //为了维护dp[0][0]
{
int left=j==0?0:dp[i][j-1];
int top=i==0?0:dp[i-1][j];
dp[i][j]=left+top;
}
}
}
return dp[m-1][n-1];
}
};
Attention
- 二维数组的定义
vector<vector<int>> asd1(row, vector<int>(column, 0)); //初始化row*column二维动态数组,初始化值为0
- 动态规划解法中,其实只需要保存
dp[i-1][j]和dp[i][j-1]两个数,还有空间优化的余地。 - 排列组合基础

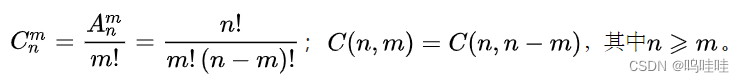

![[从零开始]用python制作识图翻译器·五](https://img-blog.csdnimg.cn/5fae92e3897f4a2f875dcb71c2ebbc60.png)