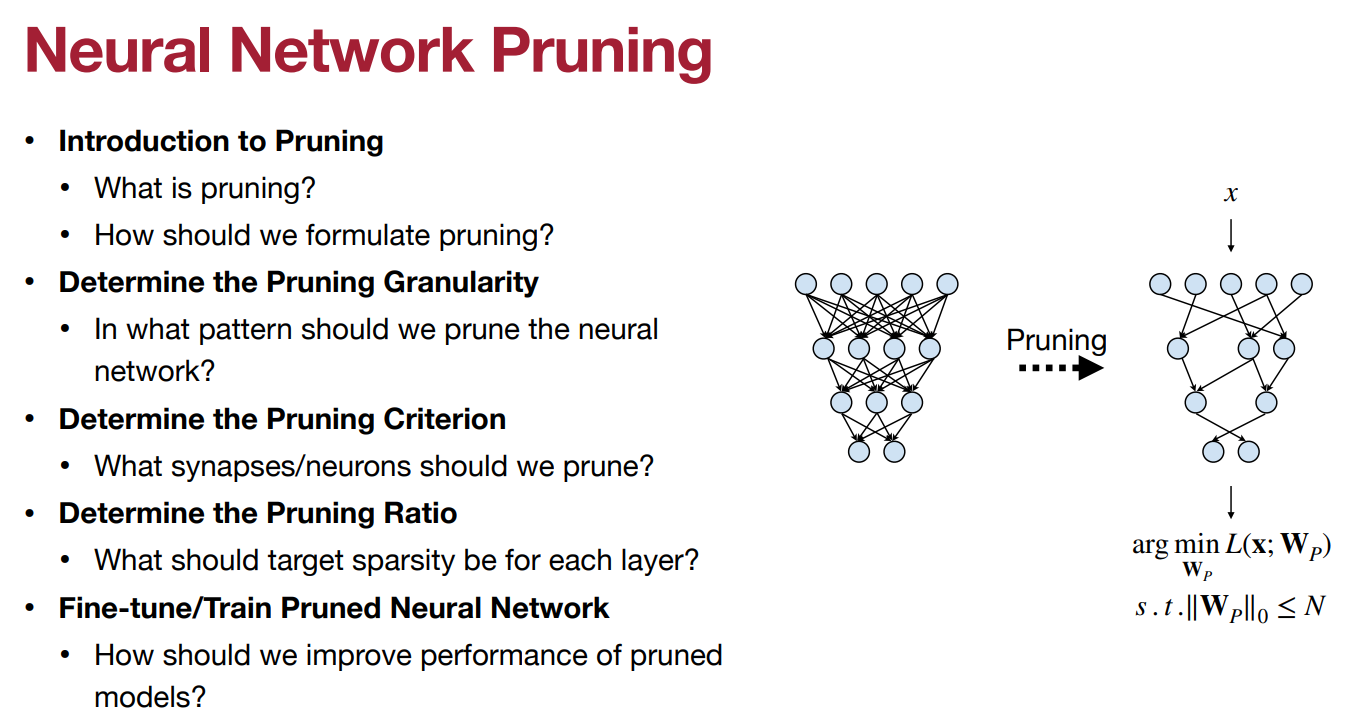
模型剪枝的介绍
修剪，消除不必要的知识。DNN的知识可以理解为存在于其权重中。
事实证明，许多 DNN 模型可以被分解为权重张量，而权重张量经常包含统计冗余（稀疏性）。因此，你可以压缩 DNN 的权重张量，从而缩小 DNN 的存储、数据传输和执行时间以及能耗成本。想想看，这就像把每个 DNN 张量放入一个 “压缩文件”，它需要的比特数比原始文件少。
然而，压缩后的权重张量仍然需要在模型推理时用于计算，所以我们需要找到一个适合高效计算的压缩方案。
许多压缩技术的工作原理是从权重张量中去除多余的零值，这样一来，压缩后的大部分或所有剩余的值都是非零的。通常情况下，使用这样的去零方案可以直接在压缩的数据上进行计算，因为我们在DNN中主要的计算是乘法/累加，对于这些零操作数是无效的。
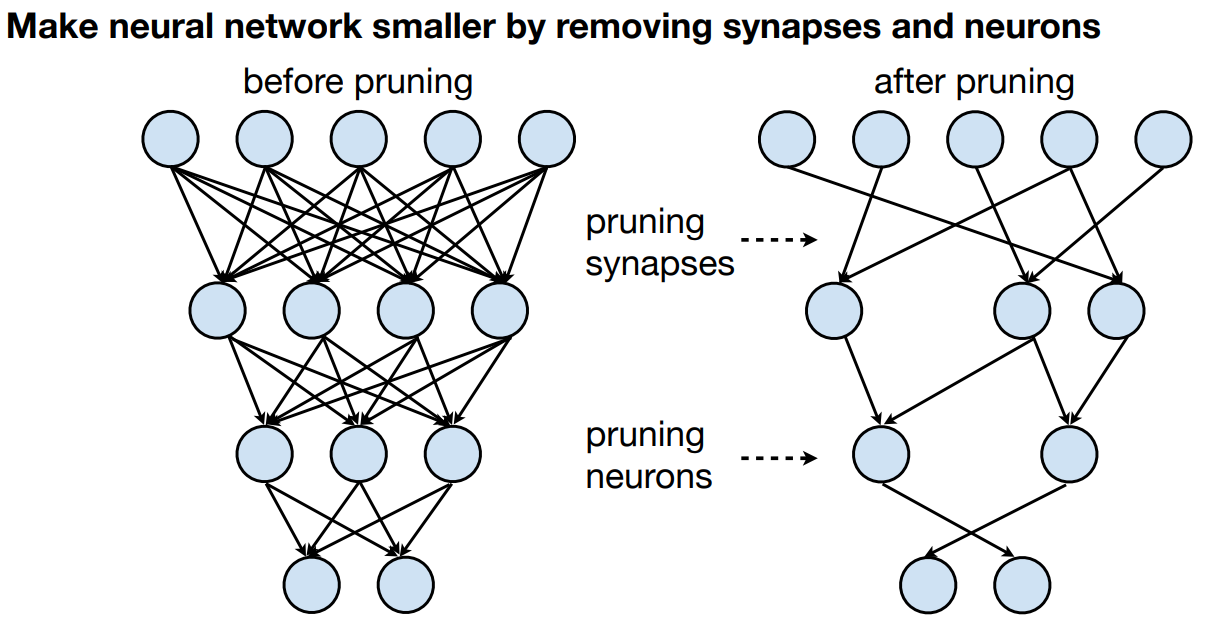然而，在许多DNN中，稀疏性并不直接以冗余零值的形式存在，而是表现为权重张量中的其他隐藏模式。于是，形成了剪枝的做法，假设张量有一些潜在的统计稀疏性，我们使用一些技术将这种稀疏性转换为零稀疏性。我们将DNN的一些权重翻转为零，并尽可能调整其他权重的值以进行补偿。由于零值权重对乘法/累加无效，我们将零值权重视为不存在（它们被 "修剪 "了），因此我们不存储、传输或计算这些权重。
因此，综上所述，我们通过将统计稀疏性转换为特定形式的稀疏性（零稀疏性），然后依靠硬件或软件来利用这种稀疏性做更少的计算，从而达到节省关键指标的目的。
通过神经生物学的类比来介绍修剪技术
在神经生物学中，轴突连接在计算和传递信息方面起重要的作用。轴突连接的数量在出生后急剧增加，并在一段时间内保持较高的水平，直到最终大量的轴突连接在青春期结束和进入成年后被破坏和消失。科学家认为，大脑这样做是为了促进生命早期的积极学习，然后在生命后期只磨练最关键的知识。这个破坏轴突连接的阶段，在神经生物学中被称为神经元轴突的 “修剪”。
因此，在深度学习中，将权重张量稀疏性转化为多余的零权重，然后对这些零权重进行处理的过程被命名为 “修剪”，类比人类发展中轴突破坏的阶段。有时，DNN在修剪前被训练完成（预训练），在这种情况下，神经生物学的类比是，模型的初始预训练就像婴儿和儿童阶段的积极努力学习，之后需要修剪，只为 "成年 "保留最重要的知识。
稀疏性
- 稀疏性通常指的是包含多个值的数据结构中的基本统计冗余度。一般来说，稀疏性意味着有机会通过减少冗余来压缩数据结构。
- 在这门课中，我们关注的数据结构是张量
- 冗余度是由计算零值元素的比例得到的
- 利用pytorch来计算模型的稀疏性
def get_sparsity(tensor: torch.Tensor) -> float:
"""
calculate the sparsity of the given tensor
sparsity = #zeros / #elements = 1 - #nonzeros / #elements
"""
return 1 - float(tensor.count_nonzero()) / tensor.numel()
def get_model_sparsity(model: nn.Module) -> float:
"""
calculate the sparsity of the given model
sparsity = #zeros / #elements = 1 - #nonzeros / #elements
"""
num_nonzeros, num_elements = 0, 0
for param in model.parameters():
num_nonzeros += param.count_nonzero()
num_elements += param.numel()
return 1 - float(num_nonzeros) / num_elements
剪枝的流程
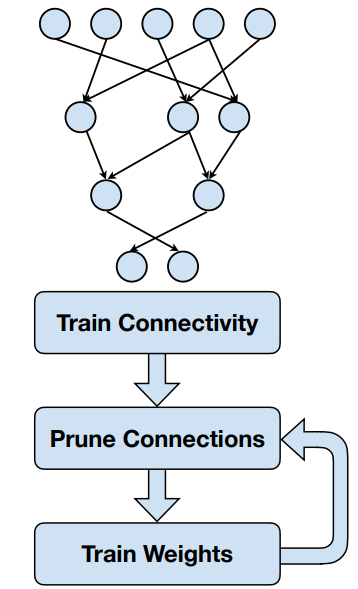
- 模型预训练，训练模型所有的权重
- 选择特定的权重来修剪✂
- 权重变为零
- 零权重可以从计算中完全跳过 ⇒ 时间（$），节省能耗
- 零权重不需要被存储 ⇒ 节省存储和数据传输
- 使用掩码来权重剪枝，掩码需要保存，训练之后还需使用它来剪枝
- 训练一轮，增强剩余权重的连接性🔗
- 梯度下降/SGD
- 在训练过程中，零权重可能会变成非零权重
- 使用之前的掩码来剪枝
- 再训练，重复以上2和3的步骤
修剪、权重更新的影响
- 在这里，我们假设使用的是magnitude-based pruning的变体，但是无论如何，想法都是相似的。
- 修剪过程的每一步都会对权重分布产生独特的影响
- 在没有其他先验知识的情况下，设想初始权重分布是高斯分布
- 修剪过程将那些绝对值接近零的权重剪掉，留下一个高于和低于零的权重值的双峰分布。
- 重新训练/微调/权重更新增加了这些分布的范围，这是因为权重调整后准确性恢复。
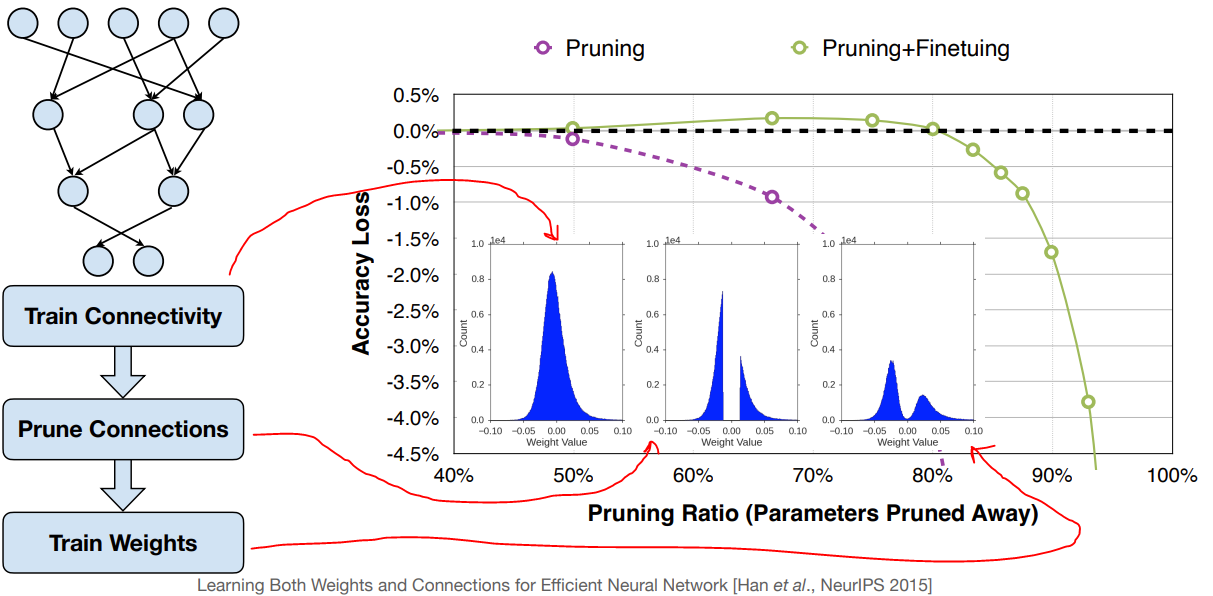
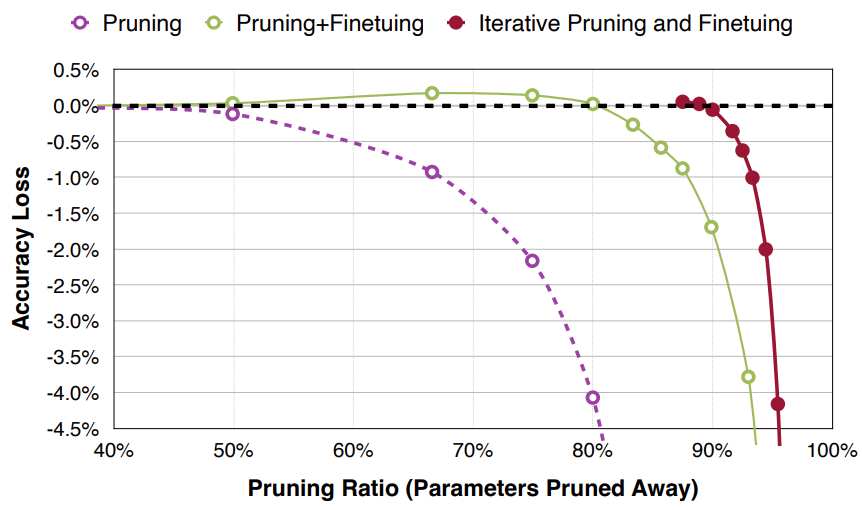
- 修剪牺牲了准确性，剪枝比例越高，对准确性的影响程度也越高
- 准确率/剪枝比例的斜率是一个渐进的过程
- 再训练/微调/权重更新可以恢复准确率
- 在非常高的剪枝比例下，准确率几乎是断崖式的下降
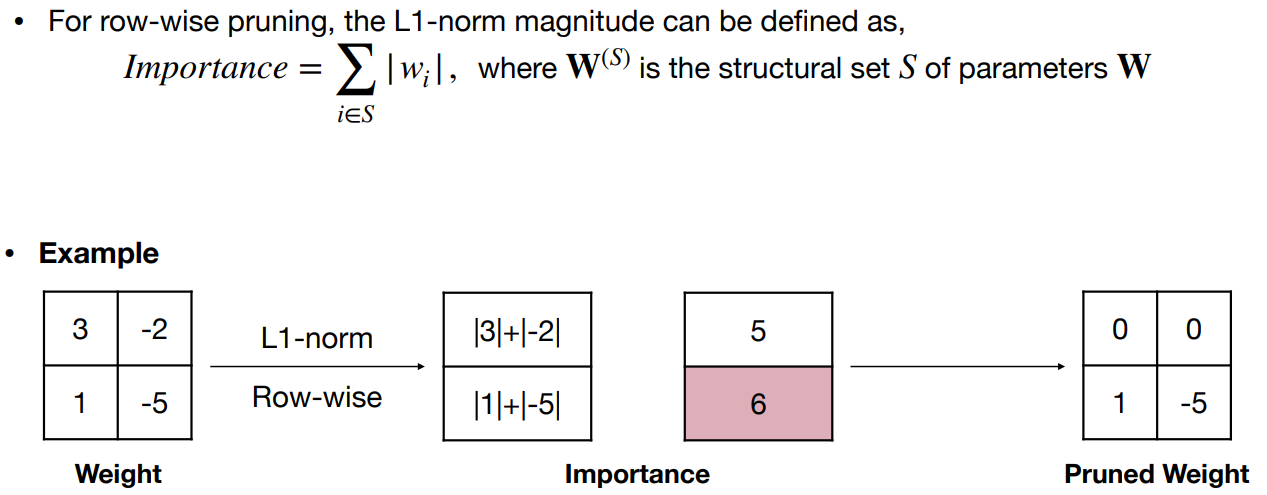
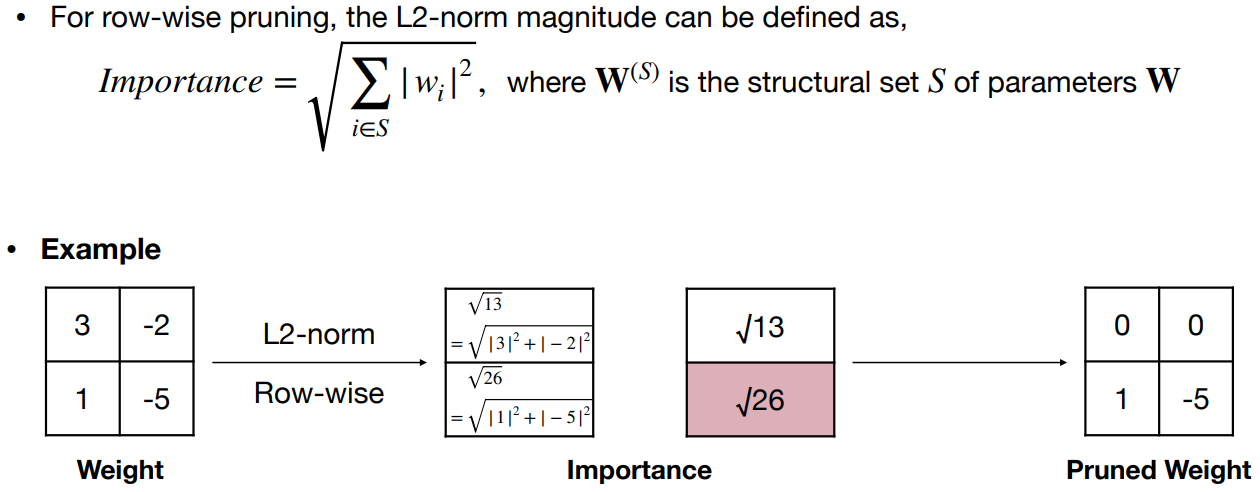
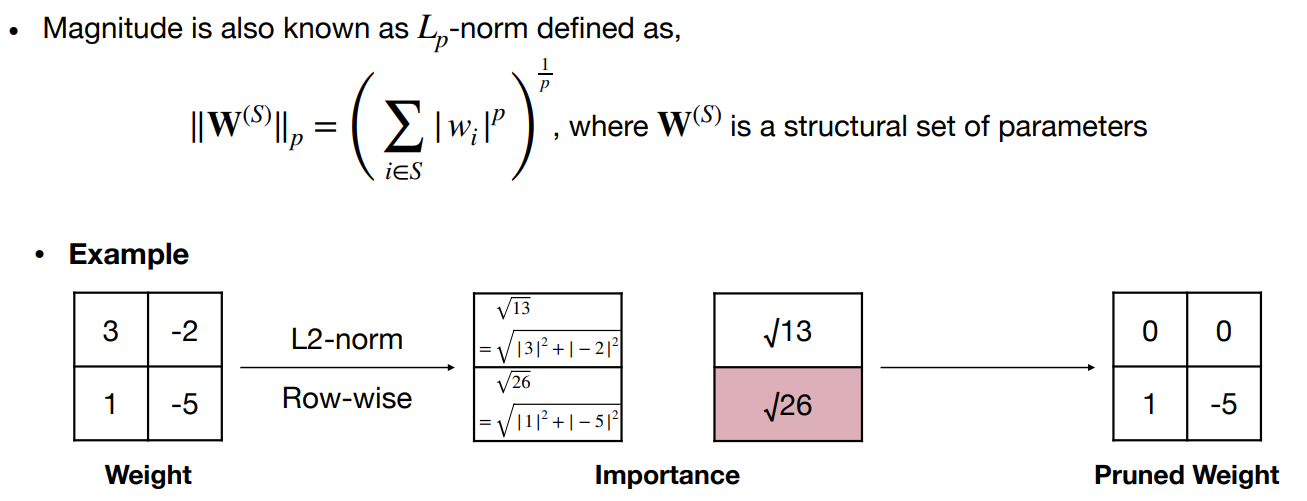
剪枝的颗粒度 Granularity
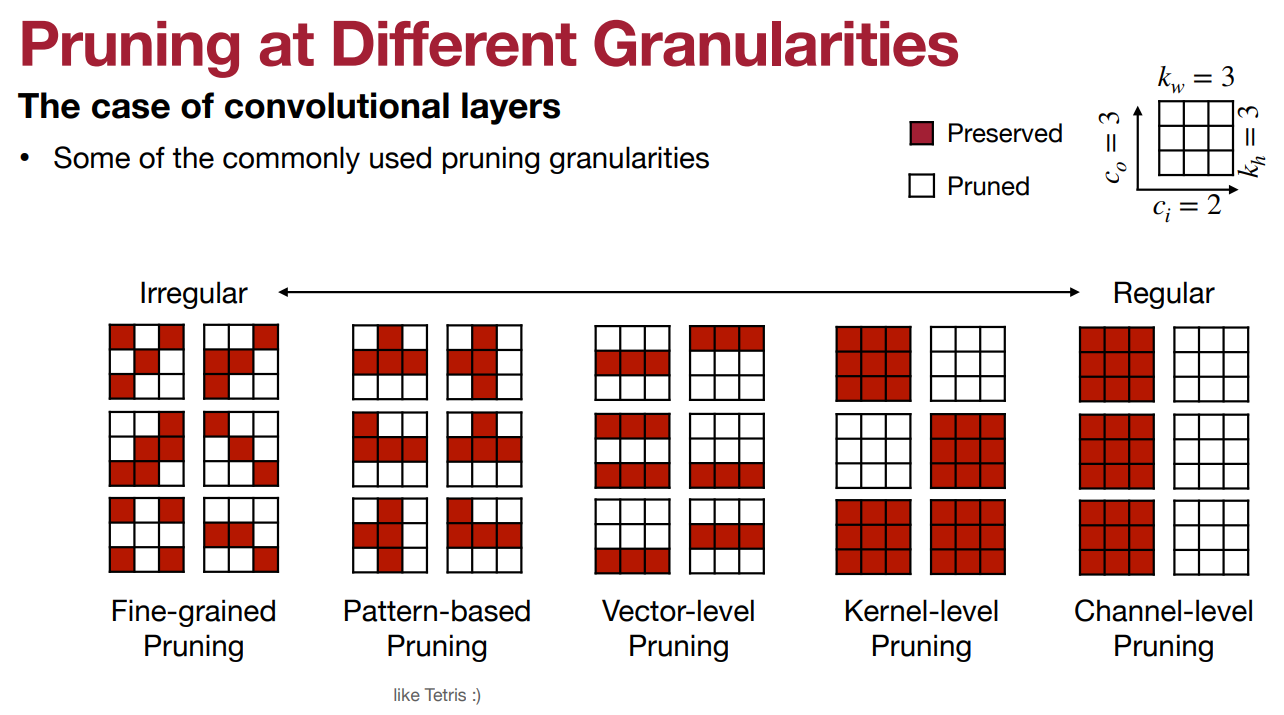
- 细粒度（又称非结构化）修剪 Fine-grained pruning
- 灵活
- 基本上是 “随机访问”，以修剪任何张量中的任何权重
- 优点
- 在相同的预训练准确率下，有较高的恢复准确率/较高的压缩率
- 缺点
- 有可能在定制硬件中利用；在CPU/GPU上有效利用具有挑战性或不可能性。
- 灵活
- 基于模式的剪枝 Pattern-based pruning
- 将剪枝指数限制为固定模式，这样硬件就更容易利用稀疏性
- 一个典型的例子是N:M块剪枝，在每个大小为M的连续权重块中，N必须为非零。
- 优点
- 更容易在硬件中加以利用
- 英伟达Ampere GPU架构利用了2:4块的稀疏性；速度大约提高了2倍
- 缺点
- 由于灵活性较低，与细粒度相比，恢复的准确性/压缩率较低
- 在CPU上有效利用可能具有挑战性
- 通道修剪 Channel pruning
- 粗粒度修剪约束，只去除整个通道，有效改变层的几何形状
- 优点
- 可以在CPU和GPU上利用（实际上是改变了层的几何形状）
- 也可以在自定义硬件中利用
- 缺点
- 由于几乎没有任何灵活性，恢复的准确率/压缩率最低
- 在细粒度和通道修剪之间
- 矢量级修剪
- 内核级修剪
修剪权重的准则 Weight-pruning criteria
基于幅度的修剪——修剪最小的权重值 Magnitude pruning - prune the smallest weight values
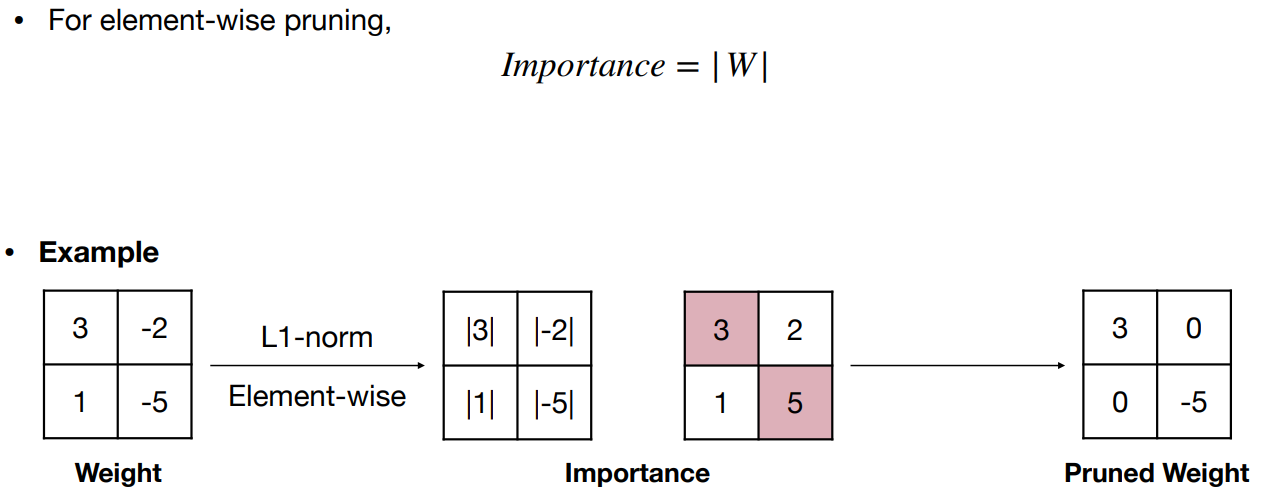
绝对值较大的权重比绝对值小的权重更重要
利用pytorch实现 基于幅值的细粒度剪枝 magnitude-based fine-grained pruning
s p a r s i t y : = # Z e r o s # W = 1 − # N o n z e r o s # W \mathrm{sparsity} := \frac {\#\mathrm{Zeros}} {\#W} = 1 - \frac {\#\mathrm{Nonzeros}} {\#W} sparsity:=#W#Zeros=1−#W#Nonzeros
式子中， # W \#W #W 是 W W W中元素的个数， # Z e r o s \#\mathrm{Zeros} #Zeros是非零元素的个数
给定目标稀疏度 s s s，权重张量 W W W乘于二进制掩码（a binary mask） M M M来忽略要去除的权重
I m p o r t a n c e = ∣ W ∣ Importance=|W| Importance=∣W∣
v t h r = kthvalue ( I m p o r t a n c e , # W ⋅ s ) v_{\mathrm{thr}} = \texttt{kthvalue}(Importance, \#W \cdot s) vthr=kthvalue(Importance,#W⋅s)
M = I m p o r t a n c e > v t h r M = Importance > v_{\mathrm{thr}} M=Importance>vthr
W = W ⋅ M W = W \cdot M W=W⋅M
I
m
p
o
r
t
a
n
c
e
Importance
Importance是
W
W
W中每个元素的绝对值，张量的形状和
W
W
W一样；
kthvalue
(
X
,
k
)
\texttt{kthvalue}(X, k)
kthvalue(X,k)找到张量
X
X
X的第
k
k
k个最小值，
v
t
h
r
v_{\mathrm{thr}}
vthr是阈值；
M
M
M中的元素只有0和1。
def fine_grained_prune(tensor: torch.Tensor, sparsity : float) -> torch.Tensor:
"""
magnitude-based pruning for single tensor
:param tensor: torch.(cuda.)Tensor, weight of conv/fc layer
:param sparsity: float, pruning sparsity
sparsity = #zeros / #elements = 1 - #nonzeros / #elements
:return:
torch.(cuda.)Tensor, mask for zeros
"""
sparsity = min(max(0.0, sparsity), 1.0)
if sparsity == 1.0:
tensor.zero_()
return torch.zeros_like(tensor)
elif sparsity == 0.0:
return torch.ones_like(tensor)
num_elements = tensor.numel()
# Step 1: calculate the #zeros (please use round())
num_zeros = round(num_elements * sparsity)
# Step 2: calculate the importance of weight
importance = tensor.abs()
# Step 3: calculate the pruning threshold
threshold = importance.view(-1).kthvalue(num_zeros).values
# Step 4: get binary mask (1 for nonzeros, 0 for zeros)
mask = torch.gt(importance, threshold)
# Step 5: apply mask to prune the tensor
tensor.mul_(mask)
return mask
说明:
- 在步骤1中，我们计算修剪后的零元素的个数（
num_zeros）。请注意，num_zeros应该是一个整数。使用round()将浮动数转换成整数。 - 在第二步，我们计算权重张量的
重要性。Pytorch提供了torch.abs(),torch.Tensor.abs(),torch.Tensor.abs_()API. - 在第三步，我们计算修剪的 “阈值”，这样所有重要性小于 "阈值 "的突触将被删除。Pytorch提供了
torch.kthvalue(),torch.Tensor.kthvalue(),torch.topk()API. - 在第四步，我们根据 "阈值 "计算修剪 “掩码”。
mask'中的**1**表示突触将被保留，mask’中的0表示突触将被删除。mask = mportance > threshold。Pytorch提供torch.gt()API。
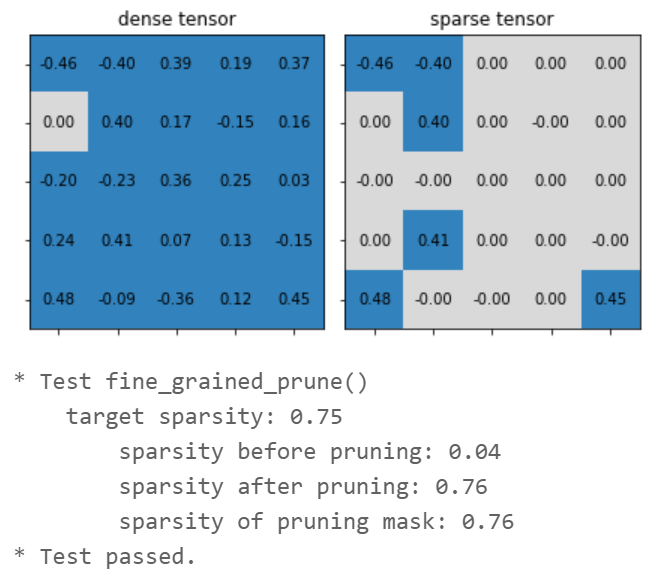
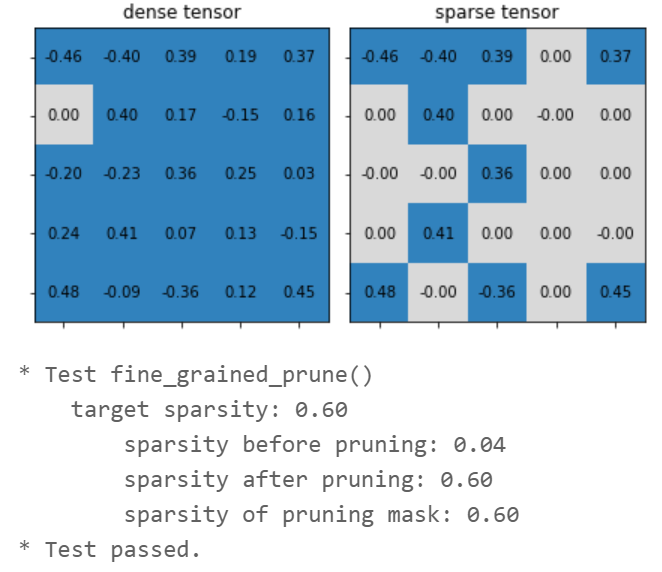
class FineGrainedPruner:
def __init__(self, model, sparsity_dict):
# keep a record of the pruning masks
# make sure the model keep sparse all the time
self.masks = FineGrainedPruner.prune(model, sparsity_dict)
@torch.no_grad()
def apply(self, model):
# pruning
for name, param in model.named_parameters():
if name in self.masks:
param *= self.masks[name]
@staticmethod
@torch.no_grad()
def prune(model, sparsity_dict):
masks = dict()
for name, param in model.named_parameters():
if param.dim() > 1: # we only prune conv and fc weights
masks[name] = fine_grained_prune(param, sparsity_dict[name])
return masks
prune the pre-trained model
pruner = FineGrainedPruner(model, sparsity)
pruner.apply(model)
fine-tune the pruned model
def train(
model: nn.Module,
dataloader: DataLoader,
criterion: nn.Module,
optimizer: Optimizer,
scheduler: StepLR,
callbacks = None,
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
) -> None:
model.train()
for inputs, targets in tqdm(dataloader, desc='train', leave=False):
# Move the data from CPU to GPU
inputs = inputs.to(device)
targets = targets.to(device)
# Reset the gradients (from the last iteration)
optimizer.zero_grad()
# Forward inference
outputs = model(inputs)
loss = criterion(outputs, targets)
# Backward propagation
loss.backward()
# Update optimizer
optimizer.step()
# use callbacks to prune model after every train
if callbacks is not None:
for callback in callbacks:
callback()
# Update scheduler
scheduler.step()
num_finetune_epochs = 5
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9, weight_decay=1e-4)
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, num_finetune_epochs)
best_sparse_checkpoint = dict()
best_sparse_accuracy = 0
print(f'Finetuning Fine-grained Pruned Sparse Model')
for epoch in range(num_finetune_epochs):
# At the end of each train iteration, we have to apply the pruning mask
# to keep the model sparse during the training
train(model, dataloader['train'], criterion, optimizer, scheduler,
callbacks=[lambda: pruner.apply(model)], device=device)
accuracy = evaluate(model, dataloader['test'], device=device)
# save the best model
is_best = accuracy > best_sparse_accuracy
if is_best:
best_sparse_checkpoint['state_dict'] = copy.deepcopy(model.state_dict())
best_sparse_accuracy = accuracy
print(f'Epoch {epoch+1} Sparse Accuracy {accuracy:.2f}% / Best Sparse Accuracy: {best_sparse_accuracy:.2f}%')
效果
预训练模型
剪枝后
微调后
![[从零开始]用python制作识图翻译器·五](https://img-blog.csdnimg.cn/5fae92e3897f4a2f875dcb71c2ebbc60.png)
