目录
- 1.概述
- 2.代码实现
- 2.1.并查集
- 2.2.邻接矩阵存储图
- 2.3.邻接表存储图
- 2.4.测试代码
- 3.应用
本文参考:
《数据结构教程》第 5 版 李春葆 主编
1.概述
(1)在一给定的无向图 G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边,而 w(u, v) 代表此边的权重,若存在 T 为 E 的子集且为无循环图,使得联通所有结点的 w(T) 最小,则此 T 为 G 的最小生成树 (minimal spanning tree)。
(2)克鲁斯卡尔 (Kruskal) 算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。假设 G = (V, E) 是一个具有 n 个顶点的带权连通无向图,T = (U, TE) 是 G 的最小生成树,则构造最小生成树的步骤如下:
- 置 U 的初值为 V(即包含有 G 中的全部顶点),TE 的初值为空集(即图 T 中的每一个顶点都构成一个分量);
- 将图 G 中的边按权值从小到大的顺序依次选取,若选取的边未使生成树 T 形成回路,则加入 TE,否则将其舍弃,直到 TE 中包含 (n - 1) 条边为止;
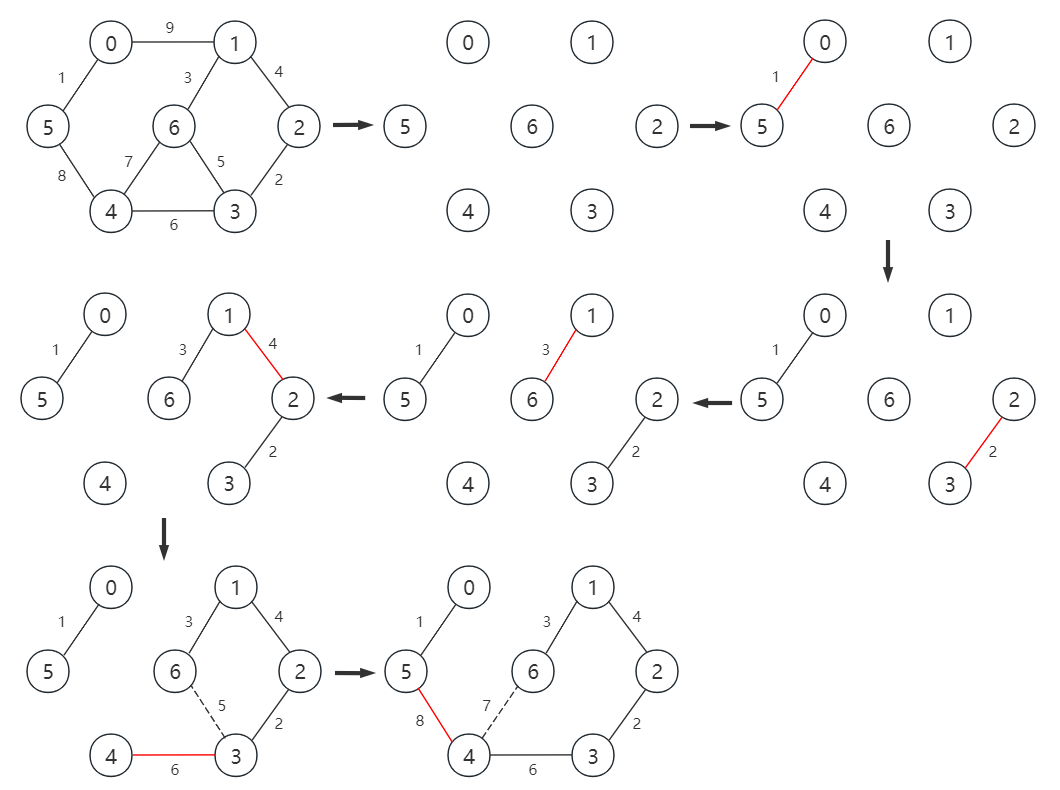
(3)例如,对带权连通无向图 G 使用克鲁斯卡尔 (Kruskal) 算法构造最小生成树的过程如下:
2.代码实现
2.1.并查集
在使用克鲁斯卡尔 (Kruskal) 算法来构造最小生成树时需要判断选择的边是否使树 T 形成回路,并还涉及到连通分量的合并,因此这里选择使用并查集来解决这个问题。有关并查集的具体知识可查看【数据结构】并查集这篇文章,并查集的代码实现如下:
//并查集
class UnionFind {
//记录连通分量(树)的个数
private int count;
//节点 x 的根节点是 root[x]
private int[] root;
//构造函数
public UnionFind(int n) {
//初始时每个节点都是一个连通分量
this.count = n;
root = new int[n];
//初始时每个节点的根节点都是其自己,即每棵树中只有一个节点
for (int i = 0; i < n; i++) {
root[i] = i;
}
}
//将 p 和 q 连通
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) {
// p 和 q 的根节点相同,它们本就是连通的,直接返回即可
return;
} else {
root[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count--;
}
}
//判断 p 和 q 是否互相连通,即判断 p 和 q 是否在同一颗树中
public boolean isConnected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
//如果 p 和 q 的根节点相同,则说明它们在同一颗树中,即它们是连通的
return rootP == rootQ;
}
//查找节点 x 的根节点
public int find(int x) {
if (root[x] != x) {
root[x] = find(root[x]);
}
return root[x];
}
//返回连通分量(树)的个数
public int getCount() {
return count;
}
}
2.2.邻接矩阵存储图
class Solution {
/**
* @param1: 邻接矩阵
* adjMatrix[i][j] = 0 表示节点 i 和 j 之间没有边直接相连;
* adjMatrix[i][j] = weight > 0 表示节点 i 和 j 之间的边的权值;
* @return: Kruskal 算法依次选择的边权值以及该边连接的两个节点
* @description: 使用 Kruskal 算法得到最小生成树
*/
public List<int[]> kruskal(int[][] adjMatrix) {
//图的节点数
int n = adjMatrix.length;
// edges 保存所有边及权重,int[] 中存储 {节点 i, 节点 j, i 和 j 之间的边的权值}
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (adjMatrix[i][j] != 0) {
edges.add(new int[]{i, j, adjMatrix[i][j]});
}
}
}
//将边按照权重进行升序排序
Collections.sort(edges, Comparator.comparingInt(a -> a[2]));
//最小生成树中所有边的权值之和
int weightSum = 0;
//保存 Kruskal 算法中依次选择的边权值以及该边连接的两个节点
List<int[]> infos = new ArrayList<>();
UnionFind uf = new UnionFind(n);
//依次遍历排序后的每一条边
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int weight = edge[2];
//选中的边会产生环,则不能将其加入最小生成树中
if (uf.isConnected(u, v)) {
continue;
}
//如果选中的边不会产生环,则它属于最小生成树
weightSum += weight;
//将节点 u 和 v 进行连通
uf.union(u, v);
infos.add(new int[]{u, v, weight});
}
System.out.println("最小生成树中边的权值之和:" + weightSum);
return infos;
}
}
2.3.邻接表存储图
class Solution {
/**
* @param1: 邻接表,List<int[]> nodes = adjList[i] 是一个 list,其中:
* nodes.get(j)[0] 表示与节点 i 相邻的第 j 个节点的编号;
* nodes.get(j)[1] 表示节点 i 与节点 nodes.get(j)[0] 之间的边权值;
* @param1: 图的节点数
* @return: kruskal 算法依次选择的边权值以及该边连接的两个节点
* @description: 使用 kruskal 算法得到最小生成树
*/
public static List<int[]> kruskal(List<int[]>[] adjList, int n) {
// edges 保存所有边及权重,int[] 中存储 {节点 i, 节点 j, i 和 j 之间的边的权值}
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < adjList.length; i++) {
// nodes 存储与节点 i 相邻的节点信息
List<int[]> nodes = adjList[i];
//遍历每个与节点 i 相邻的节点
for (int[] node : nodes) {
//节点 i 与 节点 v 相邻
int v = node[0];
// weight 为 i、v 之间的边的权值
int weight = node[1];
edges.add(new int[]{i, v, weight});
}
}
//将边按照权重进行升序排序
Collections.sort(edges, Comparator.comparingInt(a -> a[2]));
//最小生成树中所有边的权值之和
int weightSum = 0;
//保存 Kruskal 算法中依次选择的边权值以及该边连接的两个节点
List<int[]> infos = new ArrayList<>();
UnionFind uf = new UnionFind(n);
//依次遍历排序后的每一条边
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int weight = edge[2];
//选中的边会产生环,则不能将其加入最小生成树中
if (uf.isConnected(u, v)) {
continue;
}
//如果选中的边不会产生环,则它属于最小生成树
weightSum += weight;
//将节点 u 和 v 进行连通
uf.union(u, v);
infos.add(new int[]{u, v, weight});
}
System.out.println("最小生成树中边的权值之和:" + weightSum);
return infos;
}
}
2.4.测试代码
public static void main(String[] args) {
//邻接矩阵
int[][] adjMatrix = {
{0, 9, 0, 0, 0, 1, 0},
{9, 0, 4, 0, 0, 0, 3},
{0, 4, 0, 2, 0, 0, 0},
{0, 0, 2, 0, 6, 0, 5},
{0, 0, 0, 6, 0, 8, 7},
{1, 0, 0, 0, 8, 0, 0},
{0, 3, 0, 5, 7, 0, 0}
};
List<int[]> nodes1 = kruskal(adjMatrix);
for (int[] node : nodes1) {
System.out.println(node[0] + " "+ node[1] + " " + node[2]);
}
//邻接表
int n = 7;
List<int[]>[] adjList = new ArrayList[n];
for (int i = 0; i < n; i++) {
adjList[i] = new ArrayList<>();
}
adjList[0].add(new int[]{1, 9});
adjList[0].add(new int[]{5, 1});
adjList[1].add(new int[]{0, 9});
adjList[1].add(new int[]{2, 4});
adjList[1].add(new int[]{6, 3});
adjList[2].add(new int[]{1, 4});
adjList[2].add(new int[]{3, 2});
adjList[3].add(new int[]{2, 2});
adjList[3].add(new int[]{4, 6});
adjList[3].add(new int[]{6, 5});
adjList[4].add(new int[]{3, 6});
adjList[4].add(new int[]{5, 8});
adjList[4].add(new int[]{6, 7});
adjList[5].add(new int[]{0, 1});
adjList[5].add(new int[]{4, 8});
adjList[6].add(new int[]{1, 3});
adjList[6].add(new int[]{3, 5});
adjList[6].add(new int[]{4, 7});
// List<int[]> nodes2 = kruskal(adjList, 7);
// for (int[] node : nodes2) {
// System.out.println(node[0] + " "+ node[1] + " " + node[2]);
// }
}
结果如下:
最小生成树中边的权值之和:24
0 5 1
2 3 2
1 6 3
1 2 4
3 4 6
4 5 8
3.应用
(1)求图的最小生成树许多实际应用,例如城市之间的交通工程造价最优问题就是一个最小生成树问题。
(2)大家可以去 LeetCode 上找相关的最小生成树的题目来练习,或者也可以直接查看LeetCode算法刷题目录 (Java)这篇文章中的最小生成树章节。如果大家发现文章中的错误之处,可在评论区中指出。

![[从零开始]用python制作识图翻译器·五](https://img-blog.csdnimg.cn/5fae92e3897f4a2f875dcb71c2ebbc60.png)