Matlab中算法结合Simulink求解直流微电网中功率

news2025/1/11 10:09:10

 💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，博主专门做了一个专栏目录，整个专栏只放了一篇文章，足见我对其重视程度：博主专栏目录。做到极度细致，方便大家进行学习！亲民！！！还有我开了一个专栏给女朋友的，很浪漫的喔，代码学累的时候去瞧一瞧，看一看：女朋友的浪漫邂逅。有问题可以私密博主，博主看到会在第一时间回复。
📝目前更新：🌟🌟🌟电力系统相关知识，期刊论文，算法，机器学习和人工智能学习。
🚀支持：🎁🎁🎁如果觉得博主的文章还不错或者您用得到的话，可以关注一下博主，如果三连收藏支持就更好啦！这就是给予我最大的支持！                   

👨‍🎓博主课外兴趣：中西方哲学，送予读者：

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。在我这个专栏记录我有空时的一些哲学思考和科研笔记：科研和哲思。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“真理”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

📋📋📋本文目录如下：⛳️⛳️⛳️

目录

1 Simulink求解直流微电网

 2 Matlab代码算法求解直流微电网

1 Simulink求解直流微电网

包括下面三个部分：

 

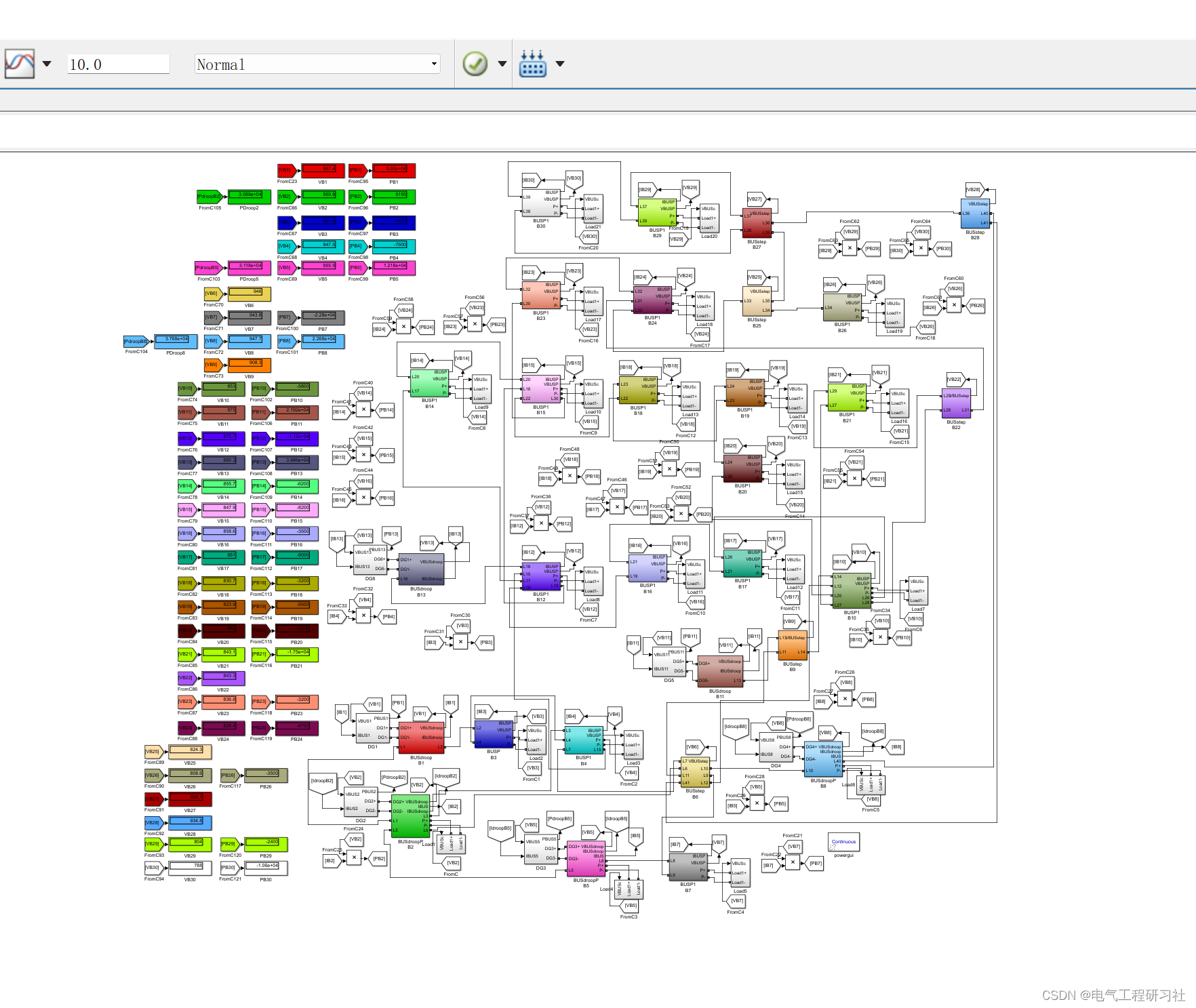
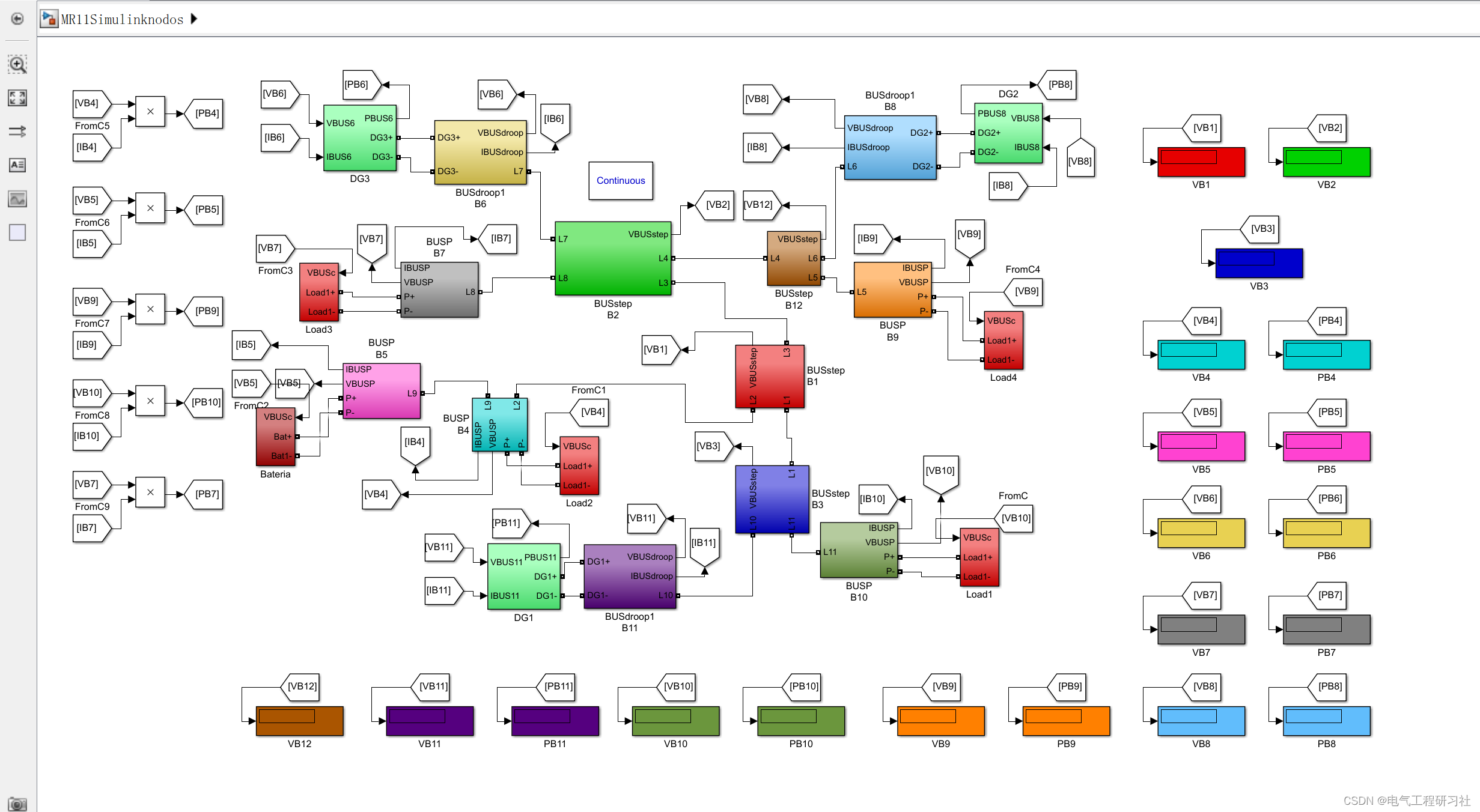
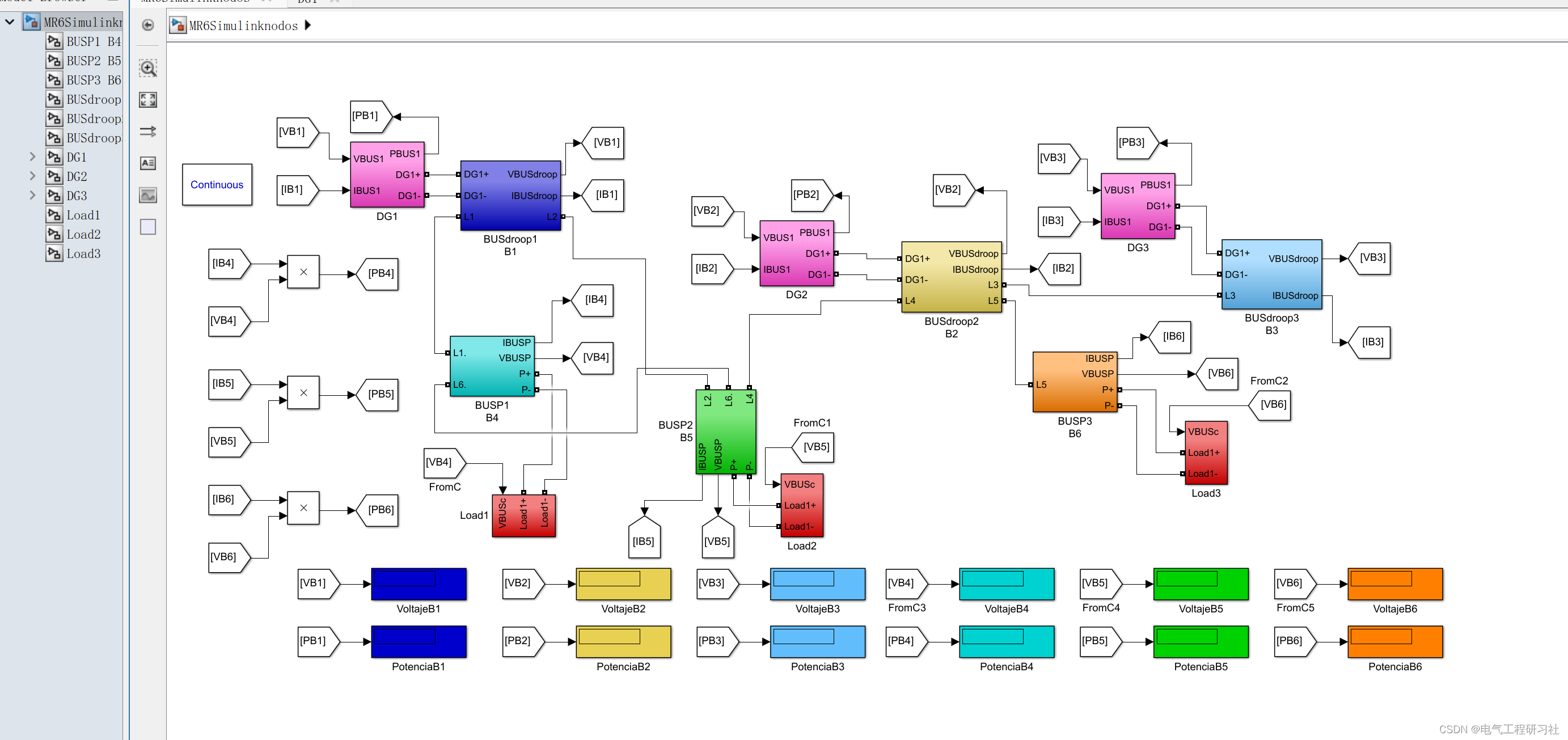
 2 Matlab代码算法求解直流微电网

部分代码： 

clear all
clc
format shortG
%% Verificaci algoritmo
% Paretros base
vref = 48;
Pbase = 500;

rlineas = 0.05; 
rbase = vref^2/Pbase;
rpu = rlineas/rbase;

step = 1;
droop = 2;
potencia = 3;
%% Datos de Lineas y Nodos
%    Lineas   i j r
        A = [ 4 1 rpu
              1 2 rpu
              2 3 rpu
              3 4 rpu];
%   nodo tipo     Potgen/gdroop  PotCarga   
B = [1   droop      rbase/0.2           0
     2   potencia    0            466.25/Pbase
     3   droop      rbase/0.5           0
     4   potencia    0             697.5/Pbase  ];

NumN = max(max(A(:,1:2))); %Nero de Nodos
NumL = length(A(:,1)); %Nero de Lineas

%% Separaci de variables

Nstep = B(find(B(:,2)==step),1); %Nodos step
Vstep = B(find(B(:,2)==step),2); %Variable step
Ndroop = B(find(B(:,2)==droop),1);%Nodos droop
Vdroop = B(find(B(:,2)==droop),2); %Variable droop
NP = B(find(B(:,2)==potencia),1);%Nodos de Pot const
Vpotencia = B(find(B(:,2)==potencia),2); %Variable Pot const

%Matriz clasificaci de variables

Var = [[Nstep; Ndroop; NP] [Vstep;Vdroop;Vpotencia]];
NumVar = length(Var);

%% Matriz Ybus y declaraci J y H 
%Cculo de Ybus
Y = zeros(NumN,NumN);
for k = 1:NumL
    n1 = A(k,1);
    n2 = A(k,2);
    ykm = 1/A(k,3);
    Y(n1,n1) = Y(n1,n1) + ykm;
    Y(n1,n2) = Y(n1,n2) - ykm;
    Y(n2,n1) = Y(n2,n1) - ykm;
    Y(n2,n2) = Y(n2,n2) + ykm;
end

v = ones(NumVar,1); %Condiciones iniciales de tensi
H=zeros(NumVar,1); %Inicializaci desajustes
J = zeros(NumVar,NumVar);%Declaraci matriz jacobiana
deltaV=zeros(NumVar,1);%Inicializaci de variaciones

%% Modo Newton Raphson
tic%contador de tiempo
%inicio de iteraciones
for j=1:10
    
%Hacer un barrido por todas las variables    
for k=1:NumVar
 %Si es step, aplicar ecuaciones step 
  if Var(k,2)==step
      pstep = 0;
      pstepl = v(Var(k,1))*(Y(Var(k,1),:)*v);
      H(Var(k,1)) = pstep-pstepl;
      for i=1:NumVar
       if Var(k,1)==i
       J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
       else
       J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
       end
      end
  else
 %Si es droop, aplicar ecuaciones droop
  if Var(k,2)==droop
      %inyecciones de potencia al nodo droop
      pgdroop = B(Var(k,1),4);
      %expresi incluyendo ecuas droop
      pdroop = B(Var(k,1),3)*(1*v(Var(k,1))-v(Var(k,1))^2);
      %potencias por las lineas
      pdroopl = v(Var(k,1))*(Y(Var(k,1),:)*v);
      %ecuaci de desajuste
      H(Var(k,1)) = pdroop-pgdroop-pdroopl;
      %Cculo de las derivadas parciales para droop k espec韋ico
      for i=1:NumVar
        %si k=i
        if Var(k,1)==i
          Jdroop = B(Var(k,1),3)*(1 - 2*v(Var(k,1)));
          Jdroopl = v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
          J(Var(k,1),i) = Jdroop - Jdroopl;
        else
          %k != i
          J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
        end
      end
  else
 %Si es potencia, aplicar ecuaciones potencia   
  if Var(k,2)==potencia
      ppot = B(Var(k,1),3)-B(Var(k,1),4); %PG-Pcarga
      ppotl = v(Var(k,1))*(Y(Var(k,1),:)*v);%Plineas
      H(Var(k,1)) = ppot-ppotl;%ecuaci髇 h(k) de potencia
      for i=1:NumVar
        %si k=i
        if Var(k,1)==i
      J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
        else
        %k != i
      J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
        end
     end
  end
  end
  end
    
end
deltaV=inv(J)*H;%vector de variacion
 v = v - deltaV;%Actalizaci髇 de variables
 I = Y*v;%calculo de corrientes nodales
 P = diag(v)*I;%potencias nodales
 %iter(j) = j;
 errAbs = abs(max(H));
end
%fin de iteraciones
t=toc%fin contador de tiempo

%% Muestra de Resultados
disp('         nodo      v(pu)         P(pu)        v(V)        P(W)')
solucion = [B(:,1)    v        P     vref*v  Pbase*P];
disp(solucion)

disp('Maximo error abs')
disp(errAbs)

clear all
clc
format shortG
%% Verificaci algoritmo
% Paretros base
vref = 48;
Pbase = 500;

rlineas = 0.05; 
rbase = vref^2/Pbase;
rpu = rlineas/rbase;

step = 1;
droop = 2;
potencia = 3;
%% Datos de Lineas y Nodos
%    Lineas   i j r
        A = [ 4 1 rpu
              1 2 rpu
              2 3 rpu
              3 4 rpu];
%   nodo tipo     Potgen/gdroop  PotCarga   
B = [1   droop      rbase/0.2           0
     2   potencia    0            466.25/Pbase
     3   droop      rbase/0.5           0
     4   potencia    0             697.5/Pbase  ];

NumN = max(max(A(:,1:2))); %Nero de Nodos
NumL = length(A(:,1)); %Nero de Lineas

%% Separaci de variables

Nstep = B(find(B(:,2)==step),1); %Nodos step
Vstep = B(find(B(:,2)==step),2); %Variable step
Ndroop = B(find(B(:,2)==droop),1);%Nodos droop
Vdroop = B(find(B(:,2)==droop),2); %Variable droop
NP = B(find(B(:,2)==potencia),1);%Nodos de Pot const
Vpotencia = B(find(B(:,2)==potencia),2); %Variable Pot const

%Matriz clasificaci de variables

Var = [[Nstep; Ndroop; NP] [Vstep;Vdroop;Vpotencia]];
NumVar = length(Var);

%% Matriz Ybus y declaraci J y H 
%Cculo de Ybus
Y = zeros(NumN,NumN);
for k = 1:NumL
    n1 = A(k,1);
    n2 = A(k,2);
    ykm = 1/A(k,3);
    Y(n1,n1) = Y(n1,n1) + ykm;
    Y(n1,n2) = Y(n1,n2) - ykm;
    Y(n2,n1) = Y(n2,n1) - ykm;
    Y(n2,n2) = Y(n2,n2) + ykm;
end

v = ones(NumVar,1); %Condiciones iniciales de tensi
H=zeros(NumVar,1); %Inicializaci desajustes
J = zeros(NumVar,NumVar);%Declaraci matriz jacobiana
deltaV=zeros(NumVar,1);%Inicializaci de variaciones

%% Modo Newton Raphson
tic%contador de tiempo
%inicio de iteraciones
for j=1:10
    
%Hacer un barrido por todas las variables    
for k=1:NumVar
 %Si es step, aplicar ecuaciones step 
  if Var(k,2)==step
      pstep = 0;
      pstepl = v(Var(k,1))*(Y(Var(k,1),:)*v);
      H(Var(k,1)) = pstep-pstepl;
      for i=1:NumVar
       if Var(k,1)==i
       J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
       else
       J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
       end
      end
  else
 %Si es droop, aplicar ecuaciones droop
  if Var(k,2)==droop
      %inyecciones de potencia al nodo droop
      pgdroop = B(Var(k,1),4);
      %expresi incluyendo ecuas droop
      pdroop = B(Var(k,1),3)*(1*v(Var(k,1))-v(Var(k,1))^2);
      %potencias por las lineas
      pdroopl = v(Var(k,1))*(Y(Var(k,1),:)*v);
      %ecuaci de desajuste
      H(Var(k,1)) = pdroop-pgdroop-pdroopl;
      %Cculo de las derivadas parciales para droop k espec韋ico
      for i=1:NumVar
        %si k=i
        if Var(k,1)==i
          Jdroop = B(Var(k,1),3)*(1 - 2*v(Var(k,1)));
          Jdroopl = v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
          J(Var(k,1),i) = Jdroop - Jdroopl;
        else
          %k != i
          J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
        end
      end
  else
 %Si es potencia, aplicar ecuaciones potencia   
  if Var(k,2)==potencia
      ppot = B(Var(k,1),3)-B(Var(k,1),4); %PG-Pcarga
      ppotl = v(Var(k,1))*(Y(Var(k,1),:)*v);%Plineas
      H(Var(k,1)) = ppot-ppotl;%ecuaci髇 h(k) de potencia
      for i=1:NumVar
        %si k=i
        if Var(k,1)==i
      J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),Var(k,1)) - Y(Var(k,1),:)*v;
        else
        %k != i
      J(Var(k,1),i) = -v(Var(k,1))*Y(Var(k,1),i);
        end
     end
  end
  end
  end
    
end
deltaV=inv(J)*H;%vector de variacion
 v = v - deltaV;%Actalizaci髇 de variables
 I = Y*v;%calculo de corrientes nodales
 P = diag(v)*I;%potencias nodales
 %iter(j) = j;
 errAbs = abs(max(H));
end
%fin de iteraciones
t=toc%fin contador de tiempo

%% Muestra de Resultados
disp('         nodo      v(pu)         P(pu)        v(V)        P(W)')
solucion = [B(:,1)    v        P     vref*v  Pbase*P];
disp(solucion)

disp('Maximo error abs')
disp(errAbs)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/172292.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

初识 jQuery（JavaScript 框架）

初识 jQuery（JavaScript 框架）

初识 jQuery（JavaScript 框架）参考描述jQuery使用 jQuery 的开发优势（部分）获取jQuery 语法基础语法入口函数$()jQuery 与 $参数DOM 与 jQuery模板获取DOM 对象jQuery 对象转换DOM 对象转换为 jQuery 对象$()jQuery 对象转换为 DO…
阅读更多...
Linux系统管理中Nginx和python的安装以及python虚拟环境软件的安装与使用（四）

Linux系统管理中Nginx和python的安装以及python虚拟环境软件的安装与使用（四）

1、Nginx的安装和配置： 说明：Nginx是一款自由的、开源的、高性能的HTTP服务器和反向代理服务器；同时也是一个IMAP、POP3、SMTP代理服务器；Nginx可以作为一个HTTP服务器进行网站的发布处理，另外Nginx可以作为反向代理进…
阅读更多...
C++：list结构算法

C++：list结构算法

List 1.元素在逻辑上具有线性次序，物理地址不做限制。 2.哨兵节点，header和trailer，封装后外部不可见。 3.重载操作符[]，实现下标和位置转换。 4.有序查找无序查找 5.前插入算法，首先创建新节点 然后使new成为this节点…
阅读更多...
设计模式之代理模式（静态动态）代理

设计模式之代理模式（静态动态）代理

前言：二十三种设计模式中的一种，属于结构型模式。它的作用就是通过提供一个代理类，让我们在调用目标方法的时候，不再是直接对目标方法进行调用，而是通过代理类间接调用。让不属于目标方法核心逻辑的代码从目标方法中剥…
阅读更多...
PHP设计模式

PHP设计模式

目录 一、使用设计模式目的 二、设计模式的七大原则 三、创建型模式（构建型模式） 1、单例模式 代码实例 2、工厂模式 2.1、工厂模式——简单工厂模式 简单工厂模式的代码实例 2.2、工厂模式——工厂方法模式 工厂方法模式的代码实例 2.3、工厂…
阅读更多...
java开发环境配置及问题排查

java开发环境配置及问题排查

Java程序必须运行在JVM之上，所以，我们第一件事情就是安装JDK。 JDK(Java Development Kit)，是Java开发工具包，它提供了Java的开发环境(提供了编译器javac等工具，用于将java文件编译为class文件)和运行环境(提 供了JVM…
阅读更多...
Java内存模型和线程安全

Java内存模型和线程安全

Java内存模型和线程安全Java内存模型引言volatile关键字synchronized关键字Java线程Java线程安全synchronized锁优化锁优化技巧列举自旋锁锁消除锁粗化具体实现轻量级锁偏向锁Java内存模型 引言 对于多核处理器而言,每个核都会有自己单独的高速缓存,又因为这多个处理器共享同一…
阅读更多...
JavaWeb-会话技术

JavaWeb-会话技术

JavaWeb-会话技术 1，会话跟踪技术的概述 对于会话跟踪这四个词，我们需要拆开来进行解释，首先要理解什么是会话，然后再去理解什么是会话跟踪: 会话:用户打开浏览器，访问web服务器的资源，会话建立&#xff…
阅读更多...
反射机制.

反射机制.

文章目录概述两个疑问关于java.lang.Class的理解获取Class实例的方式哪些类型可以有Class对象了解类的加载器掌握加载配置文件的另一种方式创建运行时类的对象体会动态性获取运行时类的完整结构调用运行时类的制定结构每日一考动态代理概述 1、反射是动态语言的关键 2、动态语…
阅读更多...
使用Docker打包镜像并发布

使用Docker打包镜像并发布

1、docker介绍 Docker 是一个开源的应用容器引擎，以镜像的形式进行发布。docker的图标是一个大鲸鱼驮着许多集装箱在海上航行。大鲸鱼就是docker，集装箱就是一个个容器。容器是完全使用沙箱机制，相互之间不会有任何接口，每个容器都…
阅读更多...
高级Spring之BeanFactory 与 ApplicationContext 的区别

高级Spring之BeanFactory 与 ApplicationContext 的区别

ApplicationContext接口 SpringBootApplication public class A01 {private static final Logger log LoggerFactory.getLogger(A01.class);public static void main(String[] args) throws NoSuchFieldException, IllegalAccessException, IOException {//启动SpringBoot程序…
阅读更多...
Python Scipy 显著性检验

Python Scipy 显著性检验

Scipy 显著性检验显著性检验（significance test）就是事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设（备择假设）是否合理，即判断总体的真实情…
阅读更多...
Linux基本功系列之userdel命令实战

Linux基本功系列之userdel命令实战

春节马上要到了，大街上到处都是张灯结彩，喜气洋洋的景象，你们那里也开始了吗？ 文章目录一. userdel命令概述二. 语法格式及常用选项语法格式及常用参数三. 参考案例3.1 删除用户但不删除家目录等相关的文件3.2 把用户彻底删除3.3 …
阅读更多...
【Linux05-进程控制】进程创建、进程等待、进程退出、进程程序替换（附简易shell实现）

【Linux05-进程控制】进程创建、进程等待、进程退出、进程程序替换（附简易shell实现）

前言 本期分享进程控制的内容。 博主水平有限，不足之处望请斧正！ 进程的控制主要分为四点： 进程创建进程退出进程等待进程程序替换 进程创建 怎么创建 通过fork创建。 #fork 是什么 创建子进程的函数。（使用已经介绍过&am…
阅读更多...
Python基础学习 -- 概念

Python基础学习 -- 概念

一、变量python的变量定义起来比较随意，不用定义数据类型a123b"123"系统会自动识别a为数值，b为字符串二、关键字定义变量名字的时候，要避开下面的关键字，但是可以通过大小写区分，as123;#错误定义As123;print…
阅读更多...
阿里云服务器ECS

阿里云服务器ECS

云服务器 ECS云服务器ECS（Elastic Compute Service）是一种简单高效、处理能力可弹性伸缩的计算服务。帮助您构建更稳定、安全的应用，提升运维效率，降低IT成本，使您更专注于核心业务创新。为什么选择云服务器ECS选择云服…
阅读更多...
音频如何分割成两段音频？这些实用方法值得收藏

音频如何分割成两段音频？这些实用方法值得收藏

有些时候，我们从网上下载的音频素材可能会出现体积较大、播放时间长等情况，而我们却只需要其中的一小段。这个时候我们就需要借助一些音频分割软件来将重要的音频片段提取出来，从而有助于缩小音频文件的占比以及存储。那么如何如何分割音频呢…
阅读更多...
JVM进修之路（一）程序计数器与虚拟机栈

JVM进修之路（一）程序计数器与虚拟机栈

JVM 定义：JVM:Java Virtual Machine，也就是Java运行时所需要的环境（Java二进制字节码运行时所需要的环境） 好处： 1.java代码一次编写，跨平台运行 2.自动内存管理，垃圾回收 3.数组下标越界检查 4…
阅读更多...
千锋Node.js学习笔记

千锋Node.js学习笔记

千锋Node.js学习笔记 文章目录千锋Node.js学习笔记写在前面1. 认识Node.js2. NVM3. NPM4. NRM5. NPX6. 模块/包与CommonJS7. 常用内置模块1. url2. querystring3. http4. 跨域jsonpcorsmiddleware（http-proxy-middleware）5. 爬虫6. events7. File System…
阅读更多...
Mysql常用命令练习（一）

Mysql常用命令练习（一）

Mysql常用命令练习（一）一、数据库的三层结构二、数据库2.1、创建数据库2.2、查看、删除数据库2.3、备份和恢复数据库三、表3.1、创建表mysql常用的数据类型(列类型)创建表查看表查看表结构练习3.2、修改表修改表名修改表的字符集添加列修改列删除列练习3…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023