来源：投稿作者：175
编辑：学姐

在深度学习中，权重的初始值非常重要，权重初始化方法甚至关系到模型能否收敛。本文主要介绍两种权重初始化方法。

为什么需要随机初始值

我们知道，神经网络一般在初始化权重时都是采用随机值。如果不用随机值，全部设成一样的值会发生什么呢？

极端情况，假设全部设成0。显然，如果某层的权重全部初始化为0，类似该层的神经元全部被丢弃(dropout)了，就不会有信息传播到下一层。

如果全部设成同样的非零值，那么在反向传播中，所有的权重都会进行相同的更新，权重被更新为相同的值，并拥有了对称(重复)的值。不管怎样进行迭代(sgd)，都不会打破这种对称性，隐藏层好像只有一个神经元，我们无法实现神经网络的表达能力。只有我们前面介绍的Dropout可以打破这种对称性。

为了打破权重的对称结构，必须随机生成初始值。

隐藏层激活值的分布

观察隐藏层激活值的分布，可以获得一些启发。

这里通过一个实验来看权重初始值是如何影响隐藏层的激活值分布的。

向一个5层神经网络（激活函数使用sigmoid函数）传入随机生成的输入数据，用直方图绘制各层激活值的数据分布。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))
    
def ReLU(x):
    return np.maximum(0, x)
    
def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    # 改变初始值进行实验！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

    a = np.dot(x, w)
    # 将激活函数的种类也改变，来进行实验！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

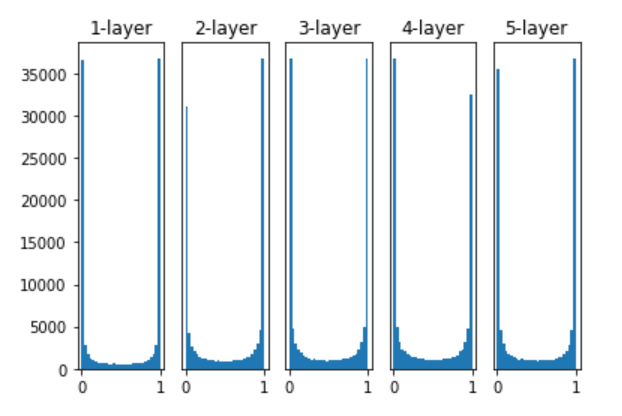
这里假设神经网络有5层，每层有100个单元。然后，用高斯分布随机生成1000个数据作为输入数据，并把它们传给5层神经网络。这里权重的初始化也通过均值为0方差为1的高斯分布。

各层的激活值呈偏向0和1的分布。这里使用的sigmoid函数是S型函数，随着输出不断地靠近0（或者靠近1，在S线的两端），它的梯度逐渐接近0。因此，偏向于0或1的数据分布会造成反向传播中梯度的值不断变小，最后消失。

我们知道，在L2正则化话会使权重参数变小，那么我们这里在初始参数的时候，直接设定一个较小的值会不会好一点。我们只要改下上面代码的27/28行。

# w = np.random.randn(node_num, node_num) * 1
w = np.random.randn(node_num, node_num) * 0.01

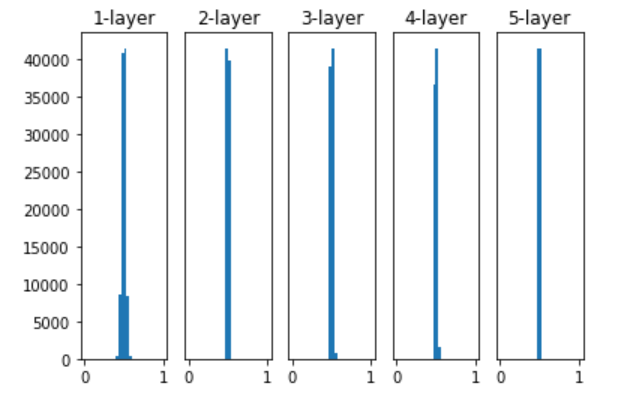
这次虽然没有偏向0和1，不会发生梯度消失的问题。但是激活值的分布有所偏向，这里集中于0.5附近。这样模型的表现力会大打折扣。

下面我们来了解比较常用的Xavier初始值和He初始值，看它们会对激活值的分布产生什么影响。

Xavier初始化

Xavier初始化的思想很简单，即尽可能保持所有层之间输入输出的方差一致。

结论是在初始化时从正态分布中随机采样来构成初始权重，其中和分别代表输入和输出的维度。

直接给出最终结果很简单，但是它是如何推导出来的呢？

下面就来推导看看，我们来看第l层的公式，假设激活函数是tanh：

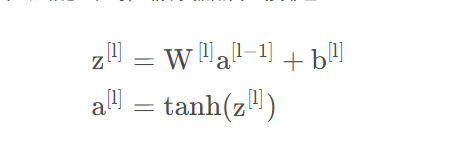
对于两独立随机变量有：

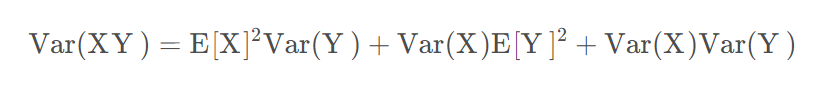
如果同时X,Y的均值为零，有：

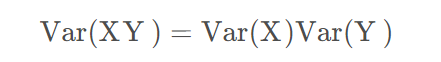
基于以上条件，那么：

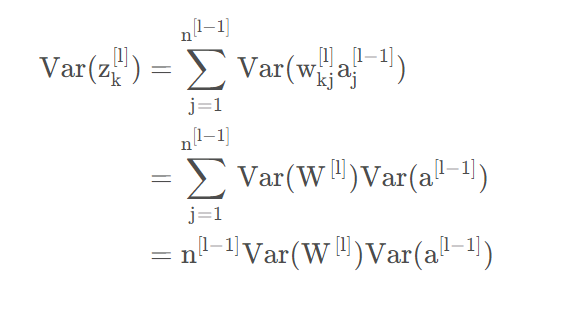
其中，基于假设1有：

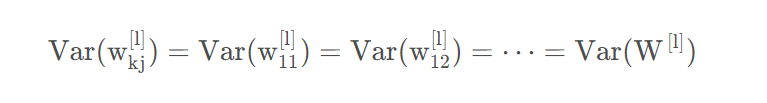
类似地，有：

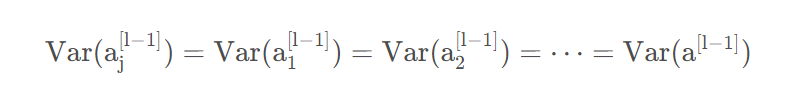
和：

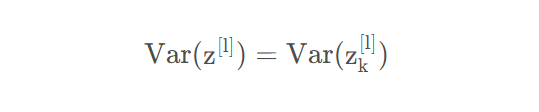
基于以上，我们有：

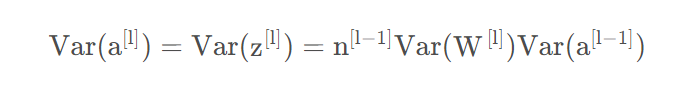
其中可以看成是输入信号，是输出信号。

也就是说，输入信号的方差经过该层后放大或缩小了倍。为了使得在经过多层网络后，输入信号不被过分放大或过分减弱，我们尽可能保持每个神经元的输入和输出方差一致，这样，需要有，即

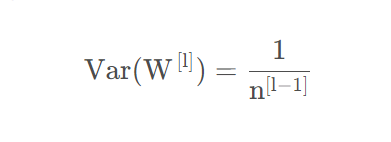
如果我们考虑整个网络，并用L代表输出层的话。那么输出层的方差与输入层方差的关系为：

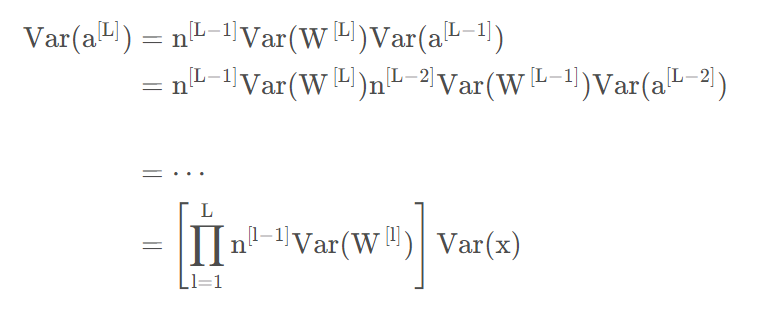
从这可以看出，我们输出和输入的方差变化取决于：

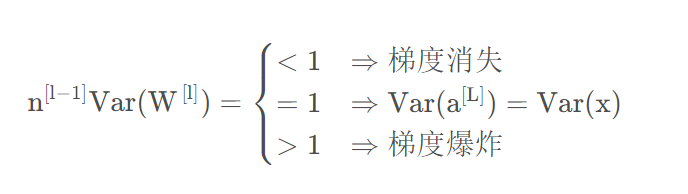
上面是正向传播过程，下面我们考虑反向传播过程。

网上大多数只有正向传播的证明，反向传播稍微复杂一点，但也不是无法证明的。

为了简化表示，我们引入一个记号：

其中C为损失。

先看第l层：

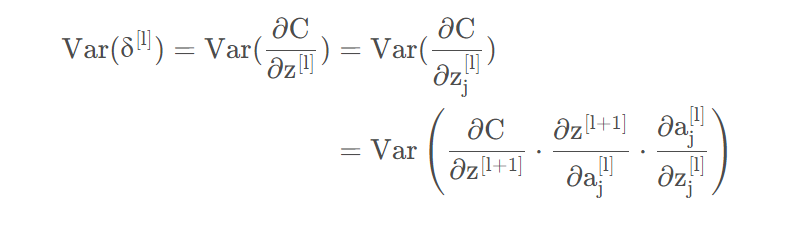
我们知道第层有个神经元，如下简单神经网络示意图所示，第二层的第j 个神经元影响了下一层的所有神经元，在计算反向传播时，需要进行梯度累积。

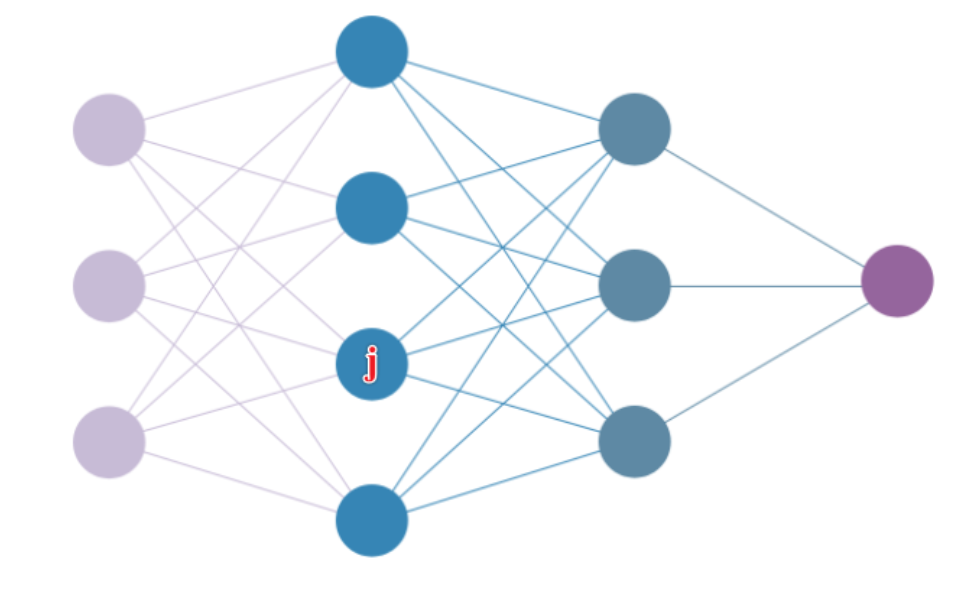
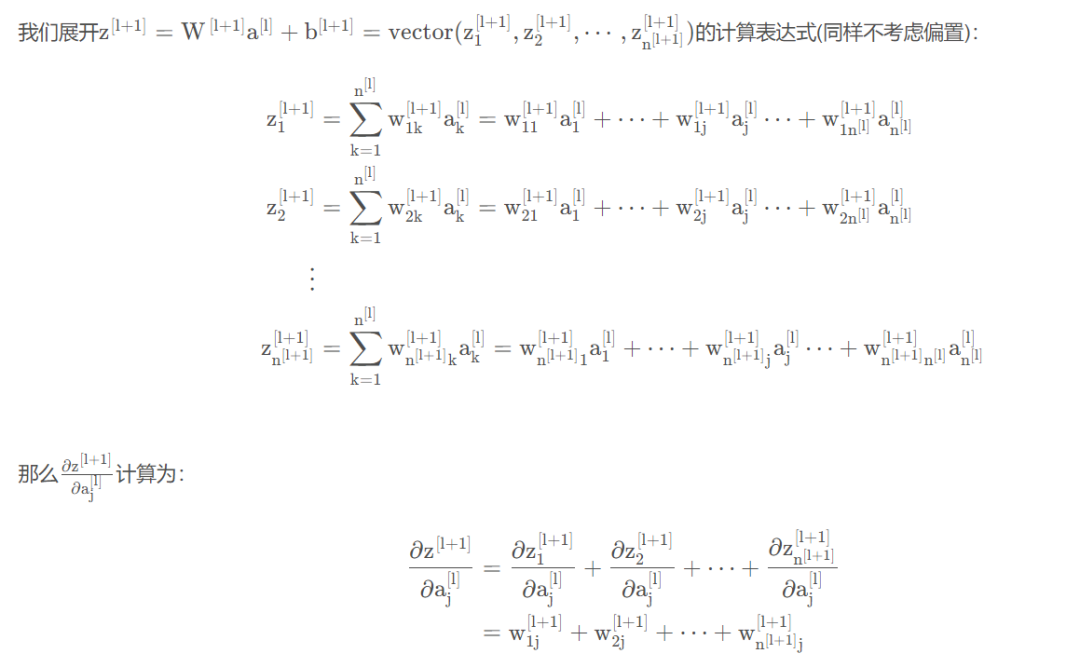
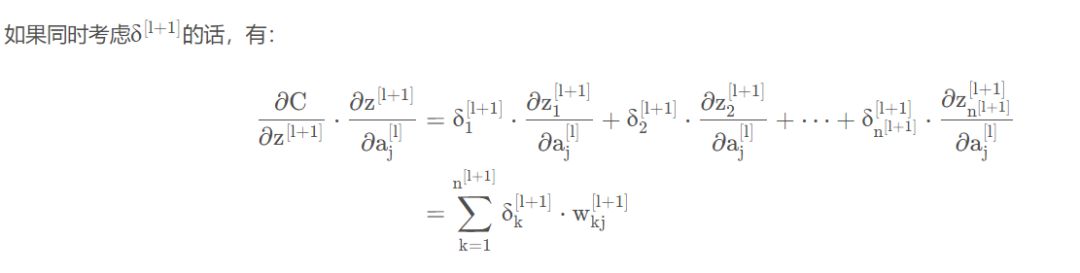
即为了让和上的梯度方差保持一致，需要有

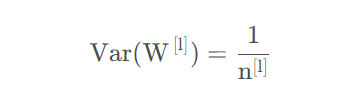
该层的输出数量。

如果我们考虑整个网络，并用L代表输出层，x代表输入向量。那么输出的梯度和输入的梯度的关系为：

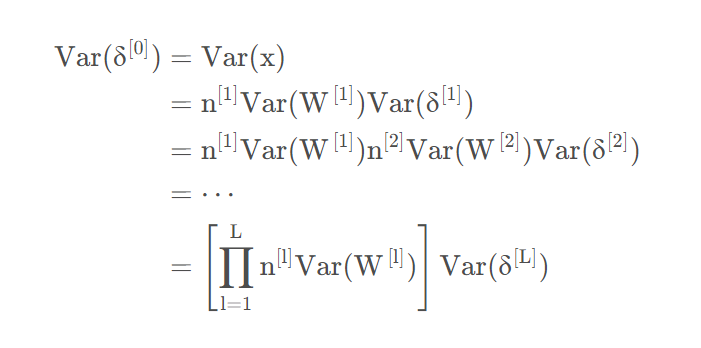
证明完毕。

为了简单(公式不好敲)，后面用和分别表示某层的输入和输出大小。

若从均匀分布中生成权重参数，那么这里的

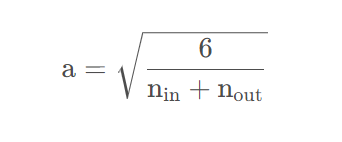
因为均匀分布的方差为:

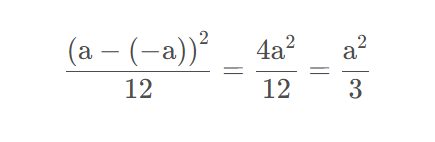
令方差等于上面的调和平均数有：

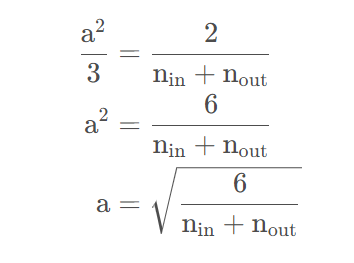
虽然在上面的推理中，我们假设激活函数为恒等函数(“不存在非线性”)在神经网络中很容易被违反，但Xavier初始化方法在实践中被证明是有效的。

继续上面的实验，我们采用Xavier初始化方法，这里输入和输出大小一致，因此取就可以了：

w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)

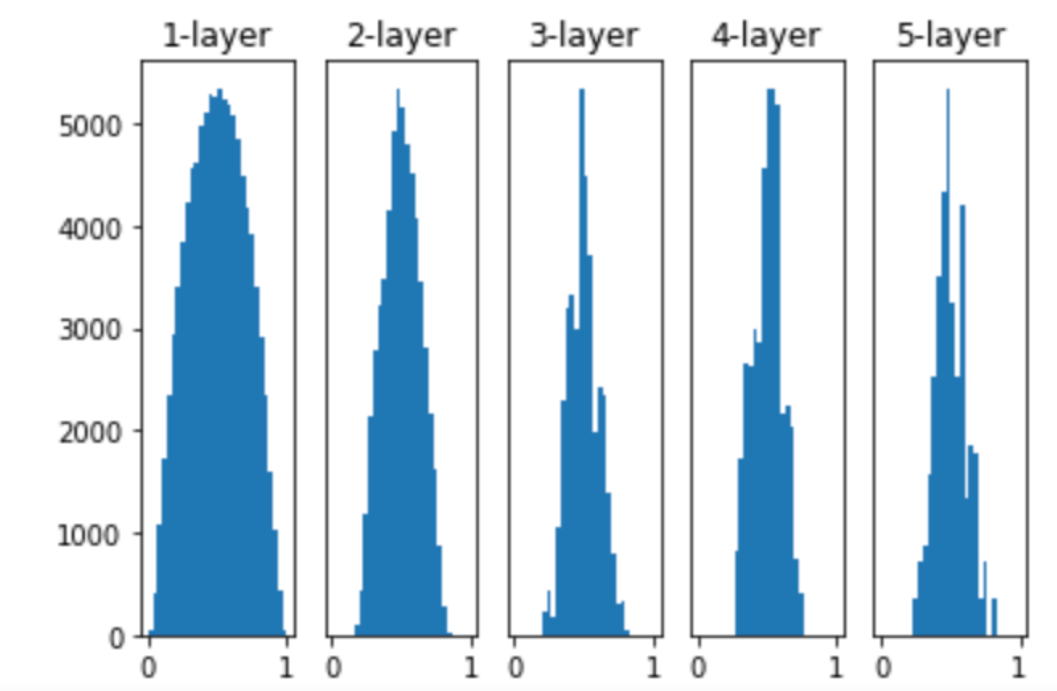
可以看到，输出值在5层之后依然保持良好的分布。我们这里使用的激活函数为sigmoid，那如果换成ReLU会怎样呢？

 z = ReLU(a)

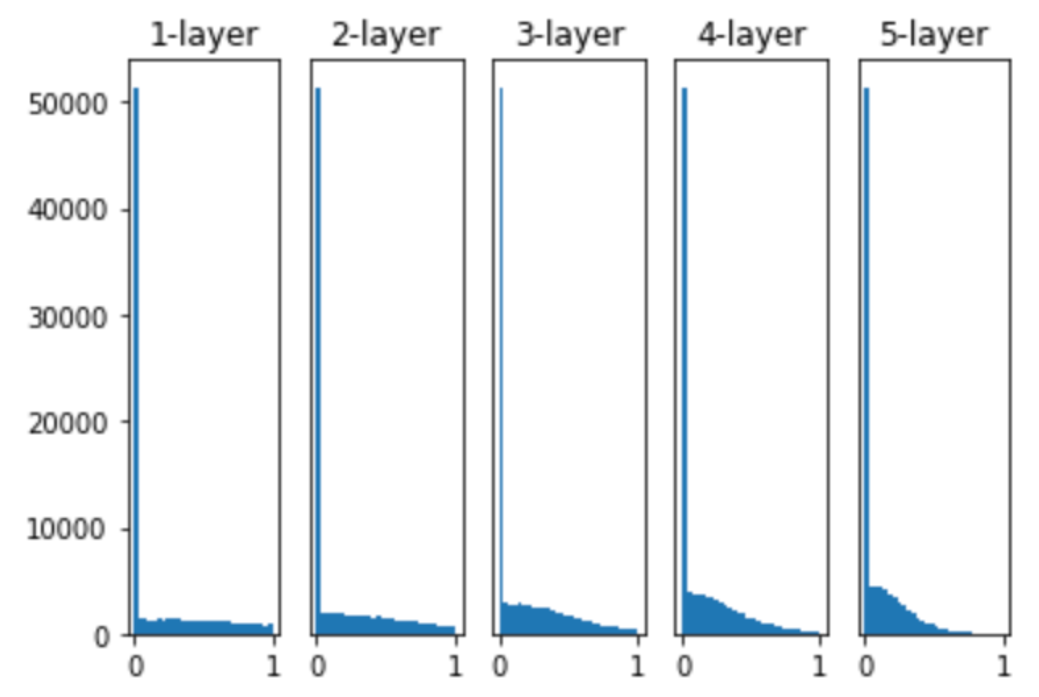
前面几层看起来还可以，随着层数的加深，偏向一点点变大。当层加深后，激活值的偏向变大，就容易出现梯度消失的问题。

那么怎么办呢？Kaiming初始化的提出就是为了解决这个问题。

Kaiming初始化

Kaiming初始化是由何凯明大神提出的，又称为He初始化。主要针对ReLU激活函数：

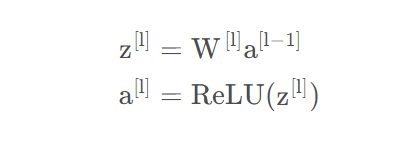
基于上面公式(4)(6)，有：

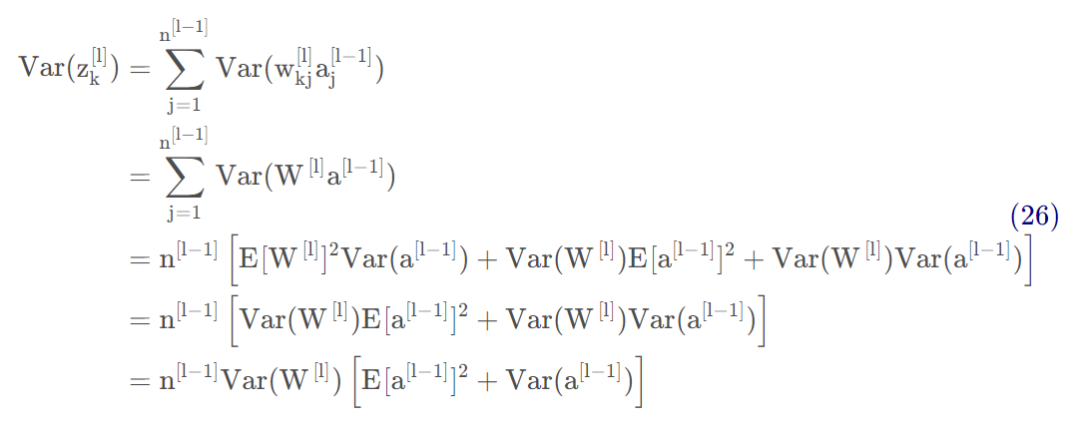
再根据方差的公式：

公式(26)可以转换为：

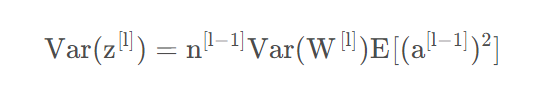
上式最后几步基于W的均值为零，所以。

所以，由公式(27)有。

把x,y用原来的式子表示，并将(29)代入式(28)得：

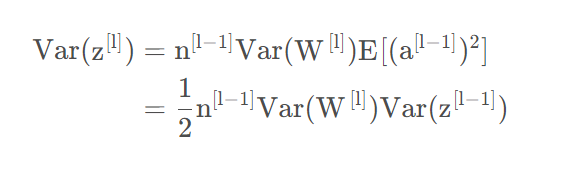
为了让和的方差一致，需要有：

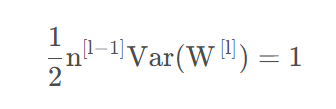
即

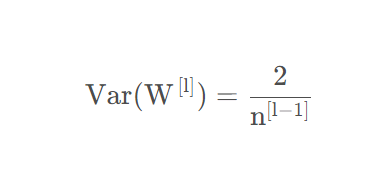
类似的，计算反向传播(注意要考虑ReLU的导数)可以得到

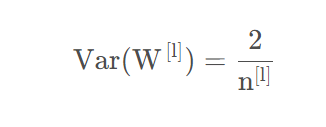
但是Kaiming初始化没有像Xaiver初始化那样取两者的调和平均数，而是根据需要任取一个即可，就像Pytorch的实现那样根据需要取输入还是输出大小。

同理如果采用均匀分布的话，那么，这里n要么是输入大小，要么是输出大小。

继续上面的实验，采用He初始化方法：

w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

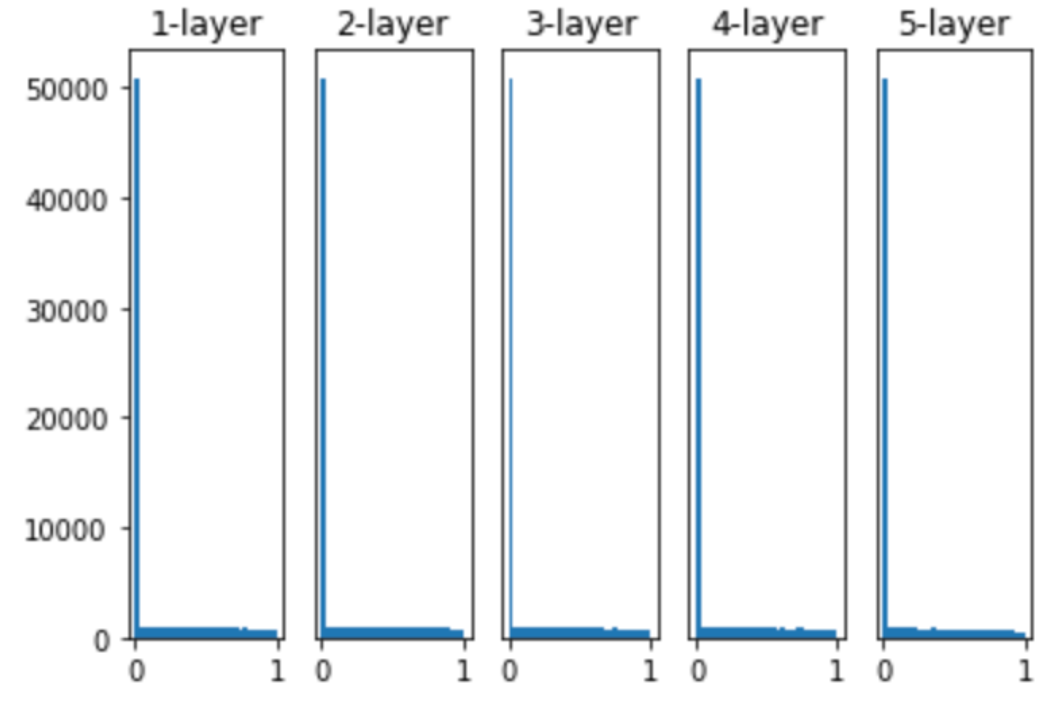
而当初始值为He初始值时，各层中分布的广度相同。由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

代码实现

代码实现就很简单了，代码地址:

👉 https://github.com/nlp-greyfoss/metagrad

class Linear(Module):
    r"""
         对给定的输入进行线性变换: :math:`y=xA^T + b`

        Args:
            in_features: 每个输入样本的大小
            out_features: 每个输出样本的大小
            bias: 是否含有偏置，默认 ``True``
        Shape:
            - Input: `(*, H_in)` 其中 `*` 表示任意维度，包括none,这里 `H_{in} = in_features`
            - Output: :math:`(*, H_out)` 除了最后一个维度外，所有维度的形状都与输入相同，这里H_out = out_features`
        Attributes:
            weight: 可学习的权重，形状为 `(out_features, in_features)`.
            bias:   可学习的偏置，形状 `(out_features)`.
        """

    def __init__(self, in_features: int, out_features: int, bias: bool = True) -> None:
        super(Linear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features

        self.weight = Parameter(Tensor.empty((out_features, in_features)))
        if bias:
            self.bias = Parameter(Tensor.zeros(out_features))
        else:
            self.bias = None
        self.reset_parameters()

    def reset_parameters(self) -> None:
        init.kaiming_normal_(self.weight)  # 默认采用kaiming初始化

    def forward(self, input: Tensor) -> Tensor:
        x = input @ self.weight.T
        if self.bias is not None:
            x = x + self.bias

        return x

我们通过调用实现的kaiming_normal_就可以采用Kaiming初始化了。