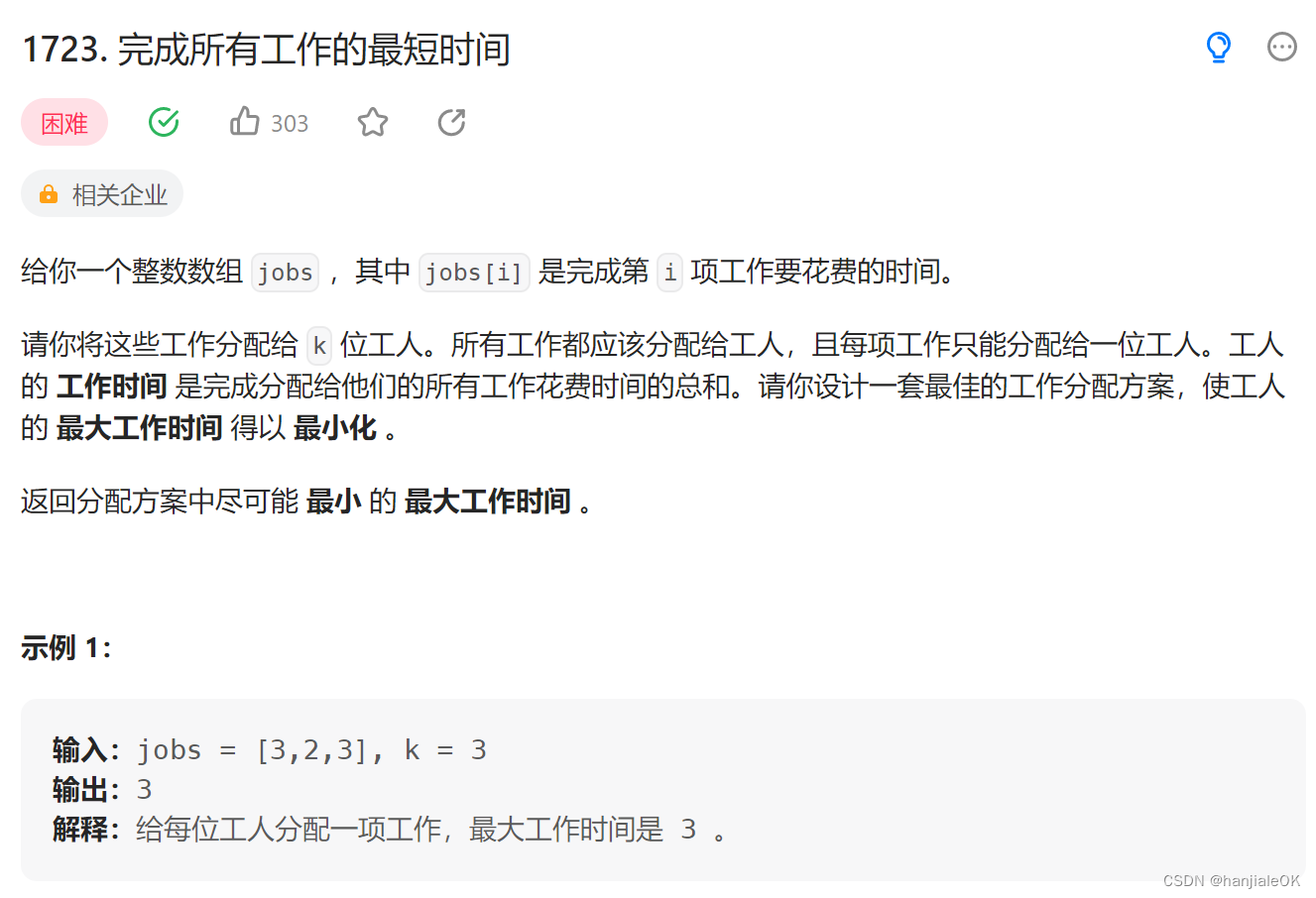
题目

题目：https://leetcode.cn/problems/find-minimum-time-to-finish-all-jobs/description/
该题和 [leetcode 2305] 公平分发饼干 完全相同。

解法

回溯+剪枝

感觉和 [leetcode 198] 划分为k个相等的子集 有点相似，这题更像是划分为k个尽量相等的子集。使用回溯的话，需要检查数据范围，即数组jobs的长度，一般不能超过 20，否则会超时。

代码基本上也是改编自 [leetcode 198]，主要是回溯+剪枝，其中有三处剪枝和一处排序比较重要：

• 如果已经超过最小值，无需继续向下递归；
• 如果当前桶和上个桶相同且该桶不是第一个，无需继续向下递归（此类题目必备剪枝）；
• 为了尽量相等，超过平均值后，无需继续向下递归；
• 数组降序排列，加快速度（此类题目必备）；

这里特别说明一下为什么需要降序排列，如果数组为 1,1,1,2,2,2，分成3组，每组的值应该为3，如果没有降序，回溯时会遇到3个1在同一个桶内，另外两个桶是2，最后一个2没法放，需要回溯到第一层栈，非常浪费时间。

class Solution {
public:
    int ans;
    void backtracking(vector<int>& jobs, vector<int>& subs, int targ, int cur) {
        int len = jobs.size();
        if (cur == len) {
            int dis = 0;
            for (int sub : subs) {
                dis = max(dis, sub);
            }
            ans = min(ans, dis);
            return ;
        }
        int n = subs.size();
        for (int i = 0; i < n; i++) {
        	// 第一处剪枝：如果已经超过最小值，无需继续向下递归
            if (subs[i] > ans) {
                return ;
            }
            // 第二处剪枝：如果当前桶和上个桶相同且该桶不是第一个，该桶无需继续向下递归
            if (i > 0 && subs[i] == subs[i-1]) {
                continue;
            }
            // 第三处剪枝：为了尽量相等，超过平均值后，无需继续向下递归
            if (subs[i] < targ) {
                subs[i] += jobs[cur];
                backtracking(jobs, subs, targ, cur+1);
                subs[i] -= jobs[cur];
            }
        }
    }
    int distributejobs(vector<int>& jobs, int k) {
        int sum = accumulate(jobs.begin(), jobs.end(), 0);
        // 降序排列，加快速度
        sort(jobs.begin(), jobs.end(), greater<int>());
        vector<int> subs(k, 0);
        int targ = sum / k;
        ans = INT_MAX;
        backtracking(jobs, subs, targ, 0);
        return ans;
    }
};

二分+回溯

一定会有一个桶分到数组最大值，故最终结果一定不低于该数组最大值；假设只有一个桶，数组中所有值只能放在该桶内，最终结果一定不超过数组总和。我们可以通过二分查找，在上面两个值范围内，找到满足题意的最小值！如何判断某个值是否满足题意（即每桶的值均不超过该值）呢，使用回溯。这种方法比上面更快，速度可以击败100%。

class Solution {
public:
    int ans;
    bool backtracking(vector<int>& jobs, vector<int>& subs, int targ, int cur) {
        int len = jobs.size();
        if (cur == len) {
            return true;
        }
        int n = subs.size();
        for (int i = 0; i < n; i++) {
        	// 剪枝：如果当前桶和上个桶相同且该桶不是第一个，该桶无需继续向下递归
            if (i > 0 && subs[i] == subs[i-1]) {
                continue;
            }
            if (subs[i] + jobs[cur] <= targ) {
                subs[i] += jobs[cur];
                bool res = backtracking(jobs, subs, targ, cur+1);
                if (res) {
                    return true;
                }
                subs[i] -= jobs[cur];
            }
        }
        return false;
    }
    int minimumTimeRequired(vector<int>& jobs, int k) {
        int sum = accumulate(jobs.begin(), jobs.end(), 0);
        // 降序排列，加快速度
        sort(jobs.begin(), jobs.end(), greater<int>());
        int low = jobs[0], high = sum;
        int ans = 0;
        while (low <= high) {
            int mid = (high + low) >> 1;
            vector<int> subs(k, 0);
            bool res = backtracking(jobs, subs, mid, 0);
            if (res) {
                high = mid - 1;
                ans = mid;
            }
            else {
                low = mid + 1;
            }
        }
        return ans;
    }
};

状压+dp