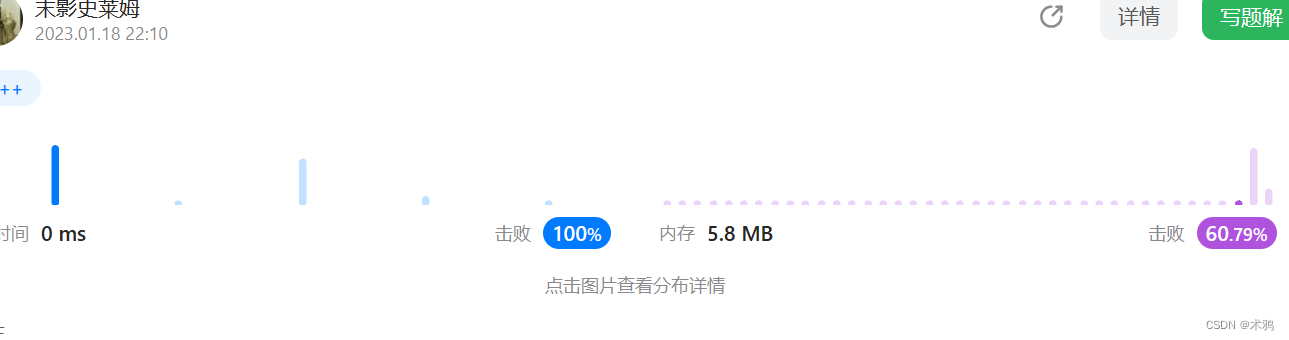
题目如下

不允许用乘除法，但是我们可以用加减法和位运算。。。不过这里不要用位运算，比如说你要是想用补码交替除法，你根本无法获得移动几位（移动31位？太鬼畜了吧）

所以说单纯的除法部分，我们可以用减法一点一点模拟，暴力不是问题。当然我们也可以使用一种叫做倍速除法的东西，快速计算出整数商 

知识点（1）倍增法：

（这个解释来自leetcode某个题解，实现就是套上两层循环） 

知识点（2）int可能会越界的问题以及处理方式

（1）第一种int可能会越界的情况，加法越界

比如说 2^31-1+2^31-1 > 2^20，这个没啥问题，但是前面太大了，没法计算，会发生越界报错

我们可以转化为a<c-b的形式

不过这个一般要求是同号，为了防止下面的情况我们常用负数，负数容纳量高一点点

（2）正负的最大值不同，如果对负数的最大值取反，结果是2^31,但因为这是补码，正数没法表示那麽大。所以我们遇到可能跃出边界的题，尽量都转化为负数，不会报错的转化方式为

 divisor= divisor>0?-divisor:divisor;

题解如下：

首先先处理唯一的特殊情况，MIN_max/-1，结果会超出界限，这个没法处理，具体题目返回具体的数值吧。

首先先记录符号位

然后把除数和被除数全部转化为负值

（结果也可能是最小值，所以说结果的计算也要是负数，比如Min-max/1的问题）

进行计算

最后按照符号位返回需要的结果

//这题很难用位运算处理。。。因为就算你用了原码交替加减法，还是不知道移动几位
    //只能说位运算是好东西但你不能天天用
    int divide(int dividend, int divisor) {
        if(dividend==-2147483648&&divisor==-1){
            return 2147483647;
        }
        bool sign=(divisor>0&&dividend>0)||(divisor<0&&dividend<0);//记录符号位
        //全部转化为负数，因为计算的时候如果用2的31次方并且转化为正数，就肯定会超出界限
        divisor= divisor>0?-divisor:divisor;
        dividend= dividend>0?-dividend:dividend;
        //下面这个是倍速除法
        int target=dividend;
        int temp;
        int result=0;
        int x=0;
        while(target<=divisor){
            temp=divisor;
            while(temp>=target-temp){//使用这种形式是为了防止越界
                x++;
                temp+=temp;
            }
            target-=temp;
            result-=pow(2,x);
            x=0;
        }
        return sign?-result:result;
    }