概述
- 说话人识别中的损失函数分为基于多类别分类的损失函数,和端到端的损失函数(也叫基于度量学习的损失函数),关于这些损失函数的理论部分,可参考说话人识别中的损失函数
- 本文主要关注这些损失函数的实现,此外,文章说话人识别中的损失函数中,没有详细介绍基于多类别分类的损失函数,因此本文会顺便补足这一点
- 本文持续更新
Softmax Loss
- 先看Softmax Loss,完整的叫法是Cross-entropy Loss with Softmax,主要由三部分组成
-
Fully Connected:将当前样本的嵌入码(embedding),变换成长度为类别数的向量(通常称为Logit),公式如下
y = W x + b y=Wx+b y=Wx+b
其中- x是特征向量,长度为 e m b e d - d i m embed\text{-}dim embed-dim
- W是权重矩阵,维度为 [ n - c l a s s e s , e m b e d - d i m ] [n\text{-}classes,embed\text{-}dim] [n-classes,embed-dim], n - c l a s s e s n\text{-}classes n-classes为类别数
- b是偏置向量,长度为 n - c l a s s e s n\text{-}classes n-classes
- Logit中的每一个值,对应W的每一行与x逐项相乘再相加,然后与b中的对应项再相加
-
Softmax:将Logit变换成多类别概率分布Probability,不改变向量长度,公式如下(取 N = n - c l a s s e s − 1 N=n\text{-}classes-1 N=n-classes−1)
y i = e x i ∑ i = 0 N e x i y_i=\frac{e^{x_i}}{\sum_{i=0}^{N}e^{x_i}} yi=∑i=0Nexiexi
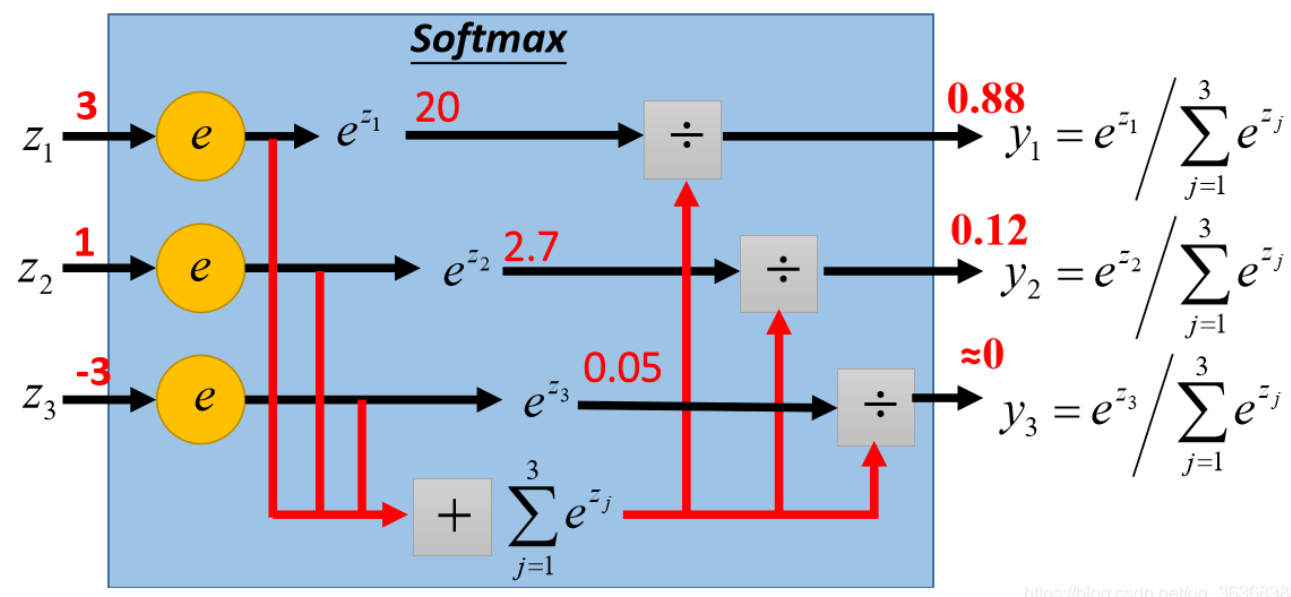
- 本质上是max函数的软化版本,将不可导的max函数变得可导
- 因此需要像max函数那样,具有最大值主导的特点,上图中
s o f t m a x ( [ 3 , 1 , − 3 ] ) = [ 0.88 , 0.12 , 0 ] softmax([3,1,-3])=[0.88,0.12,0] softmax([3,1,−3])=[0.88,0.12,0] - 又因为输出是多类别概率分布,因此Probability的每一项相加等于1
∑ i = 0 N y i = 1 \sum_{i=0}^{N}y_i=1 i=0∑Nyi=1 - 但是当Logit的值都比较小时,比如:
[
0
,
1
]
[0,1]
[0,1],最大值主导的效果不明显
s o f t m a x ( [ 0.1 , 0.3 , 0.5 , 0.7 , 0.9 ] ) = [ 0.1289 , 0.1574 , 0.1922 , 0.2348 , 0.2868 ] softmax([0.1,0.3,0.5,0.7,0.9])=[0.1289, 0.1574, 0.1922, 0.2348, 0.2868] softmax([0.1,0.3,0.5,0.7,0.9])=[0.1289,0.1574,0.1922,0.2348,0.2868]
-
Cross-entropy(交叉熵):将Ground Truth(基本事实)的One-hot Vector(记为 P P P)与Probability(记为 Q Q Q)计算相似度,输出是标量。交叉熵的值越小,Probability与One-hot Vector越相似,公式如下
L C E ( P , Q ) = − ∑ i = 0 N p i log ( q i ) L_{CE}(P,Q)=-\sum_{i=0}^{N} p_i \log(q_i) LCE(P,Q)=−i=0∑Npilog(qi)- One-hot Vector的长度与Probability一致,即等于类别数 N N N,形式为 [ 0 , 0 , . . . , 1 , . . . , 0 ] [0,0,...,1,...,0] [0,0,...,1,...,0],即GT是哪个类,哪个类对应的下标就为1
- 设One-hot Vector值为1的下标为
j
j
j,上式可简化为
L S o f t m a x ( P , Q ) = − log ( q j ) = − log ( e x j ∑ i = 0 N e x i ) L_{Softmax}(P,Q)=-\log(q_j)=-\log(\frac{e^{x_j}}{\sum_{i=0}^{N}e^{x_i}}) LSoftmax(P,Q)=−log(qj)=−log(∑i=0Nexiexj)
-
- 在上述的过程中,如果用tensor.scatter_来实现One-hot Vector是比较难懂的,完整PyTorch代码如下
import torch import torch.nn.functional as F import torch.nn as nn embed_dim = 5 num_class = 10 device = torch.device("cuda" if torch.cuda.is_available() else "cpu") x = torch.tensor([0.1, 0.3, 0.5, 0.7, 0.9]) x.unsqueeze_(0) # 模拟batch-size,就地在dim = 0插入维度,此时x的维度为[1,5] x = x.expand(2, embed_dim) # 直接堆叠x,使batch-size = 2,此时x的维度为[2,5] x = x.float().to(device) # label是长度为batch-size的向量,每个值是GT的下标,维度为[2] label = torch.tensor([0, 5]) label = label.long().to(device) weight = nn.Parameter(torch.FloatTensor(num_class, embed_dim)).to(device) nn.init.xavier_uniform_(weight) # 初始化权重矩阵 logit = F.linear(x, weight) # 取消偏置向量 probability = F.softmax(logit, dim=1) # 维度为[2,10] # one_hot的数据类型与设备要和x相同,维度和Probability相同[2,10] one_hot = x.new_zeros(probability.size()) # 根据label,就地得到one_hot,步骤如下 # scatter_函数:Tensor.scatter_(dim, index, src, reduce=None) # 先把label的维度变为[2,1],然后根据label的dim = 1(参数中的src)上的值 # 作为one_hot的dim = 1(参数中的dim)上的下标,并将下标对应的值设置为1 # 由于label的dim = 1上的值只有一个,所以是One-hot,如果label维度为[2,2],则为Two-hot # 如果label维度为[2,k],则为K-hot one_hot.scatter_(1, label.view(-1, 1).long(), 1) # 等价于 # one_hot = F.one_hot(label, num_class).float().to(device) # 但是F.one_hot只能构造One-hot,Tensor.scatter_可以构造K-hot # 对batch中每个样本计算loss,并求均值 loss = 0 for P, Q in zip(one_hot, probability): loss += torch.log((P * Q).sum()) loss /= -one_hot.size()[0] # 等价于 # loss = F.cross_entropy(logit, label) - 上述PyTorch代码要看懂,是之后魔改Softmax Loss的基础
AAM-Softmax(ArcFace)
-
AAM-Softmax(Additive Angular Margin Loss,也叫ArcFace)出自人脸识别,是说话人识别挑战VoxSRC近年冠军方案的基础损失函数,是基于Softmax Loss进行改进而来的。步骤如下
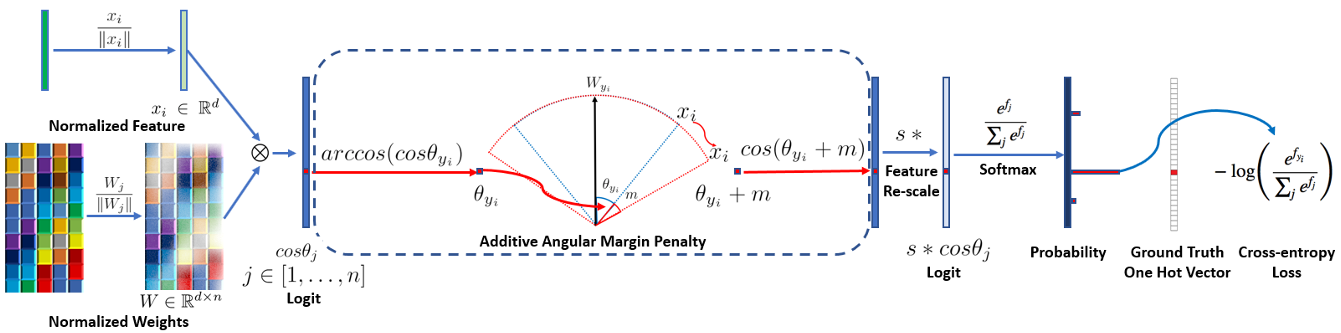
-
取消偏置向量,根据上文,Logit中的每一个值,对应W的每一行 w i w_i wi与x逐项相乘再相加,即 y i = w i x y_i=w_ix yi=wix
-
把 w i w_i wi和 x x x都单位化
w i ′ = w i ∣ ∣ w i ∣ ∣ , x ′ = x ∣ ∣ x ∣ ∣ w'_i=\frac{w_i}{||w_i||},x'=\frac{x}{||x||} wi′=∣∣wi∣∣wi,x′=∣∣x∣∣x -
计算Logit,此时Logit中的每一个值如下,即 w i w_i wi和 x x x的夹角的余弦值,记为 θ i \theta_i θi
y i = w i ′ x ′ = w i ∣ ∣ w i ∣ ∣ x ∣ ∣ x ∣ ∣ = cos < w i , x > = cos θ i y_i=w'_ix'=\frac{w_i}{||w_i||}\frac{x}{||x||}=\cos<w_i,x>=\cos\theta_i yi=wi′x′=∣∣wi∣∣wi∣∣x∣∣x=cos<wi,x>=cosθi -
权重矩阵W的每一行,本质上是神经网络学习到的每个说话人的中心向量(中心点),关于说话人的中心点,可参考说话人识别中的损失函数中的端到端损失函数。端到端的损失函数,直接利用每个batch中属于不同说话人的样本,计算对应说话人的中心点;而基于多类别分类的损失函数,则是通过学习,得到每个说话人的中心点
-
因此,将 w i w_i wi和 x x x单位化后,再计算Softmax Loss,可以视作是对当前样本嵌入码与每一个说话人中心点,计算余弦相似度向量,对余弦相似度向量进行Softmax Loss优化。根据上文,当Logit的值都比较小时,比如: [ 0 , 1 ] [0,1] [0,1],Softmax最大值主导的效果不明显,所以单位化后计算的Logit,需要进行伸缩(Scale),即 y i = s ∗ y i = s cos θ i y_i=s*y_i=s\cos\theta_i yi=s∗yi=scosθi。此时再计算Softmax Loss,如下
L = − log ( e s cos θ j ∑ i = 0 N e s cos θ i ) L=-\log(\frac{e^{s\cos\theta_j}}{\sum_{i=0}^{N}e^{s\cos\theta_i}}) L=−log(∑i=0Nescosθiescosθj) -
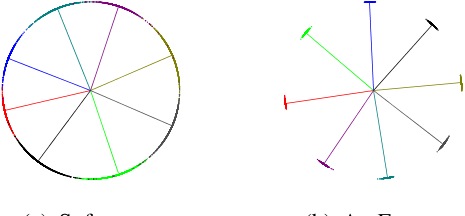
用此时的Softmax Loss,训练2维嵌入码,然后取8个类,对这8个类的大量样本,计算嵌入码,绘制到图上,如下面左图所示。发现这8个类类间是可分的,但是类内却没有聚合,我们希望这8个类能够像下面右图那样,不仅类间可分,而且类内聚合
-
首先要明确:两个向量的夹角范围为 [ 0 , π ] [0,\pi] [0,π],夹角余弦值范围为 [ − 1 , 1 ] [-1,1] [−1,1],并且单调递减,如下图所示
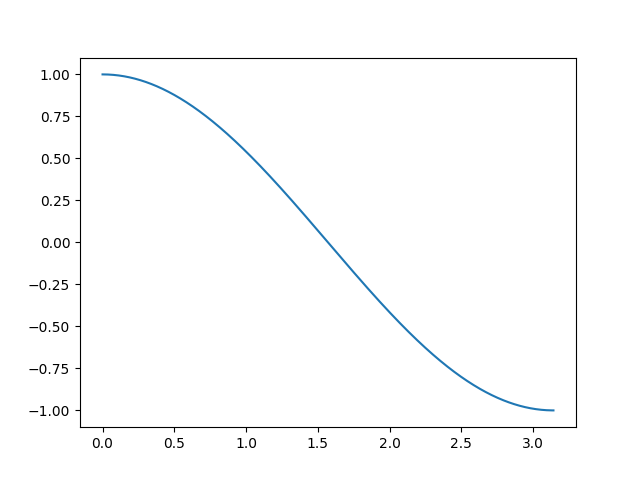
-
训练时,对嵌入码和GT说话人中心点的夹角,施加额外的惩罚,惩罚后,该夹角变大,从而余弦值变小,神经网络需要将余弦值重新变大,才能使该嵌入码正确分类。测试时,用嵌入码与不同的嵌入码直接计算相似度,此时没有惩罚,从而实现类间可分和类内聚合
-
AAM-Softmax中,直接将GT夹角加上一个值 m m m(通常称为margin),从而Logit中GT对应的值变为 y j = s cos ( θ j + m ) y_j=s\cos(\theta_j+m) yj=scos(θj+m),Logit中其他的值不变,仍为 s cos θ i s\cos\theta_i scosθi。此时再计算Softmax Loss,如下
L = − log ( e s cos ( θ j + m ) e s cos ( θ j + m ) + ∑ i = 0 , i ≠ j N e s cos θ i ) L=-\log(\frac{e^{s\cos(\theta_j+m)}}{e^{s\cos(\theta_j+m)}+\sum_{i=0,i\ne j}^{N}e^{s\cos\theta_i}}) L=−log(escos(θj+m)+∑i=0,i=jNescosθiescos(θj+m))
-
-
在上述的过程中,施加额外的惩罚这一步,有不同的情况需要讨论,先看forward函数
def forward(self, input, label): # input即上述的x,label与上述要求一致 # 计算cos(theta),F.normalize默认对dim = 1施加l2-norm cosine = F.linear(F.normalize(input), F.normalize(self.weight)) # 计算sin(theta) sine = torch.sqrt(1.0 - torch.pow(cosine, 2)) # cos(theta-m) = cos(theta)cos(m) - sin(theta)sin(m) phi = cosine * self.cos_m - sine * self.sin_m # easy_margin表示只将cos(theta) > 0的余弦值惩罚为cos(theta-m) # cos(theta) <= 0的余弦值仍为cos(theta) # 惩罚后的余弦值,范围为[-1, cos(m)] if self.easy_margin: phi = torch.where(cosine > 0, phi, cosine) # 否则,对全区间施加惩罚,但不都是惩罚为cos(theta-m) # 取th = -cos(m) # 将cos(theta) > th的余弦值惩罚为cos(theta-m) # 将cos(theta) <= th的余弦值惩罚为cos(theta) + cos(m) - 1 # 惩罚后的余弦值,范围为[cos(m) - 2, cos(m)] else: ######## # 主流代码会将cos(theta) <= th的余弦值 # 惩罚为m*sin(m),难以理解,在此不采用 # phi = torch.where(cosine > self.th, phi, cosine - self.mm) phi = torch.where(cosine > self.th, phi, cosine - self.mmm) ######## # 构造One-hot Vector one_hot = input.new_zeros(cosine.size()) one_hot.scatter_(1, label.view(-1, 1).long(), 1) # 只有GT对应的余弦值被惩罚,其他余弦值仍为cos(theta) output = (one_hot * phi) + ((1.0 - one_hot) * cosine) # 伸缩 output *= self.scale # 返回的是logit return output -
如果采用easy-margin,会导致GT余弦值较大的不连续
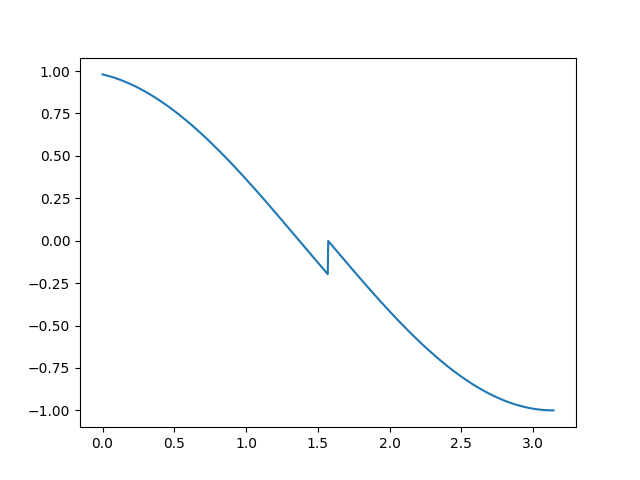
-
不采用easy-margin,GT余弦值能变得连续
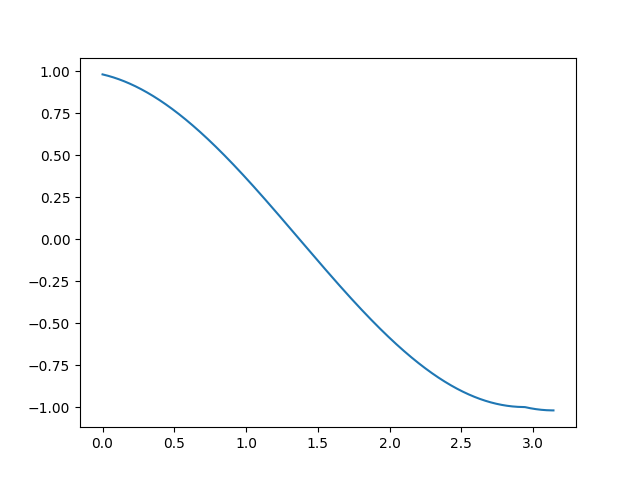
-
最后是AAM-Softmax的完整PyTorch代码
class ArcMarginProduct(nn.Module): r"""Implement of large margin arc distance: : Args: in_features: size of each input sample out_features: size of each output sample scale: norm of input feature margin: margin cos(theta + margin) """ def __init__(self, in_features, out_features, scale=32.0, margin=0.2, easy_margin=False): super(ArcMarginProduct, self).__init__() self.in_features = in_features self.out_features = out_features self.scale = scale self.margin = margin self.weight = nn.Parameter(torch.FloatTensor(out_features, in_features)) nn.init.xavier_uniform_(self.weight) self.easy_margin = easy_margin self.cos_m = math.cos(margin) self.sin_m = math.sin(margin) self.th = math.cos(math.pi - margin) self.mm = math.sin(math.pi - margin) * margin self.mmm = 1.0 + math.cos( math.pi - margin) # this can make the output more continuous ######## self.m = self.margin ######## # update函数可用于margin调度,类似学习率调度,只不过margin是越调度越大 def update(self, margin=0.2): self.margin = margin self.cos_m = math.cos(margin) self.sin_m = math.sin(margin) self.th = math.cos(math.pi - margin) self.mm = math.sin(math.pi - margin) * margin self.m = self.margin self.mmm = 1.0 + math.cos(math.pi - margin) # self.weight = self.weight # self.scale = self.scale def forward(self, input, label): cosine = F.linear(F.normalize(input), F.normalize(self.weight)) sine = torch.sqrt(1.0 - torch.pow(cosine, 2)) phi = cosine * self.cos_m - sine * self.sin_m if self.easy_margin: phi = torch.where(cosine > 0, phi, cosine) else: ######## # phi = torch.where(cosine > self.th, phi, cosine - self.mm) phi = torch.where(cosine > self.th, phi, cosine - self.mmm) ######## one_hot = input.new_zeros(cosine.size()) one_hot.scatter_(1, label.view(-1, 1).long(), 1) output = (one_hot * phi) + ((1.0 - one_hot) * cosine) output *= self.scale return output def extra_repr(self): return '''in_features={}, out_features={}, scale={}, margin={}, easy_margin={}'''.format(self.in_features, self.out_features, self.scale, self.margin, self.easy_margin)
Sub-center ArcFace
- 数据集常常带有噪声,越是大的数据集,噪声越是多,常见的噪声有离群点(Outlier)噪声和标签翻转(Label-flip)噪声,关于数据噪声,可参考说话人识别的数据需求中“数据的正确性”这一节
- 大数据集的噪声清除是非常困难且昂贵的,神经网络需要能够在带有噪声(CASIA Face中噪声约有9.3%-13.0%)的数据集中,甚至是强噪声(MS1MV0中噪声约有47.1%-54.4%)的数据集中,进行训练
- Sub-center ArcFace就是用于在带有噪声的大规模数据集训练中,要求类内聚合和类间可分(即严格性Strictness),同时不被数据集中的噪声过度影响(即鲁棒性Robustness),的损失函数,步骤如下
-
根据上文,权重矩阵W的每一行,本质上是神经网络学习到的每个说话人的中心点,但是在带有噪声的数据集中, 这个学习到的中心点,可能不是非常准确
-
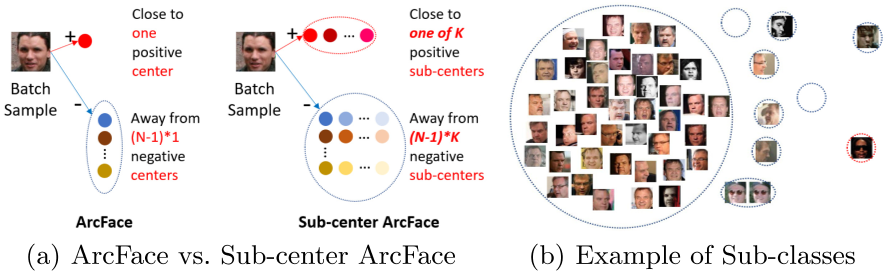
可以让神经网络学习每个说话人的 K K K个中心点,其中一个是正常样本(Easy clean)的中心点,称为主导中心点(Dominant Sub-center),其余是噪声(Hard or Noise)样本的中心点,称为非主导中心点(Non-dominant Sub-center)。如下图(b)所示,取 K = 10 K=10 K=10,则一共有10个圆圈,最大圆圈为主导中心点,其余圆圈为非主导中心点
-
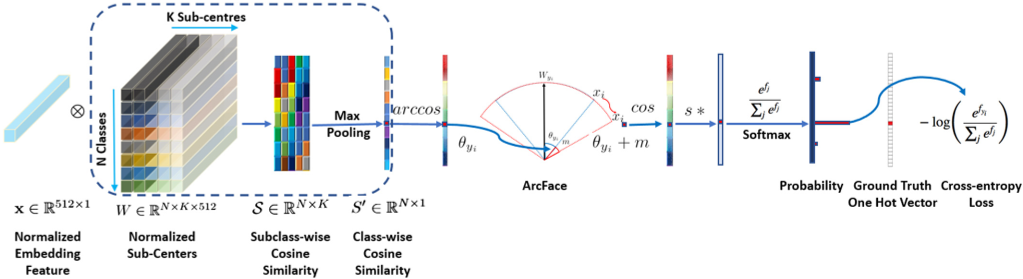
由此,W的维度从 [ n - c l a s s e s , e m b e d - d i m ] [n\text{-}classes,embed\text{-}dim] [n-classes,embed-dim]变成了 [ n - c l a s s e s , e m b e d - d i m , K ] [n\text{-}classes,embed\text{-}dim,K] [n-classes,embed-dim,K],将嵌入码和W的每个中心点,计算余弦相似度,会得到维度为 [ n - c l a s s e s , K ] [n\text{-}classes,K] [n-classes,K]的相似度矩阵
-
对相似度矩阵的每一行进行池化,会得到长为 n - c l a s s e s n\text{-}classes n-classes的向量,可以作为Logit,后续的步骤与ArcFace一致。Sub-center ArcFace的额外处理,集中在下图的蓝色虚线内
-
上述对相似度矩阵的池化操作,就是平衡损失函数的Strictness和Robustness的关键。我们知道,ArcFace是对Logit中嵌入码和GT中心点的夹角,加上margin,再取cos得到GT相似度,最后对Logit计算Softmax Loss
-
因此,要分析margin与池化的协同作用,需要先把相似度矩阵映射成夹角矩阵,再作分析,如下图所示

-
其中
- min ( i n t e r ) \min(inter) min(inter)表示对当前非GT的 ( N − 1 ) ∗ K (N-1)*K (N−1)∗K个夹角进行最小值池化
- max ( i n t e r ) \max(inter) max(inter)表示对当前非GT的 ( N − 1 ) ∗ K (N-1)*K (N−1)∗K个夹角进行最大值池化
- min ( i n t r a ) \min(intra) min(intra)表示对当前GT的 K K K个夹角进行最小值池化
- max ( i n t r a ) \max(intra) max(intra)表示对当前GT的 K K K个夹角进行最大值池化
- (1) 表示,取嵌入码与距离最近的GT夹角,加上margin,再取cos得到GT相似度;取嵌入码与距离最近的非GT夹角,再取cos得到非GT相似度。此时对类内聚合的Strictness降低,从而对离群点噪声的Robustness提高;对类间可分的Strictness提高,从而对标签翻转噪声的Robustness一般
- (2) 表示,取嵌入码与距离最近的GT夹角,加上margin,再取cos得到GT相似度;取嵌入码与距离最远的非GT夹角,再取cos得到非GT相似度。此时对类内聚合的Strictness降低,从而对离群点噪声的Robustness提高;对类间可分的Strictness降低,从而对标签翻转噪声的Robustness提高。但此时训练无法收敛,因为监督信息不够强,梯度方向不明确
- (3) 表示,取嵌入码与距离最远的GT夹角,加上margin,再取cos得到GT相似度;取嵌入码与距离最近的非GT夹角,再取cos得到非GT相似度。此时对类内聚合的Strictness提高,从而无法学习出多个Sub-center,导致对噪声Robustness弱;对类间可分的Strictness提高。此时效果类似原始ArcFace
- (4) 表示,取嵌入码与距离最远的GT夹角,加上margin,再取cos得到GT相似度;取嵌入码与距离最远的非GT夹角,再取cos得到非GT相似度。此时对类内聚合的Strictness提高,从而无法学习出多个Sub-center,导致对噪声Robustness弱;对类间可分的Strictness降低
-
综上,(1) 是较优的做法,但是较大的 K K K(如 K = 10 K=10 K=10),会破坏类内聚合,因为正常样本中,许多困难样本被用于学习非主导中心点,因此常取 K = 3 K=3 K=3。为增强类内聚合,还可以在神经网络判别能力较强时,去除非主导中心点,只保留主导中心点,即 K = 1 K=1 K=1,同时去除与GT主导中心点夹角小于75度的样本(这些样本可视为噪声),再用剩下的样本进行训练
-
- 如何检验Sub-center ArcFace的效果呢?我们希望的效果是:简单和困难样本越靠近主导中心点越好,噪声样本越靠近非主导中心点越好。因此,要检验Sub-center ArcFace的效果,可以先用强噪声的大规模数据集训练Sub-center ArcFace,之后统计训练集中,更靠近主导中心点,与更靠近非主导中心点的样本,最后检查这些样本中,哪些是正常样本,哪些是噪声样本。如下图所示

- 从上图中可见,相比ArcFace(图c),Sub-center ArcFace靠近主导中心点(图a)的噪声样本从38%降低到12%,不过也有4%左右的正常样本,更靠近非主导中心点(图b)
- 绝大多数的靠近主导中心点的噪声样本,夹角都大于75度,这也是上述Sub-center ArcFace最后一个步骤中的增强类内聚合,按照75度来去除噪声样本的依据。采用增强类内聚合方法后,效果如图(d)所示
- 有了ArcFace的基础,Sub-center ArcFace的PyTorch实现就比较好理解了,下面是完整代码
class ArcMarginProduct_subcenter(nn.Module): r"""Implement of large margin arc distance with subcenter: Reference: Sub-center ArcFace: Boosting Face Recognition by Large-Scale Noisy Web Faces. https://ibug.doc.ic.ac.uk/media/uploads/documents/eccv_1445.pdf Args: in_features: size of each input sample out_features: size of each output sample scale: norm of input feature margin: margin cos(theta + margin) K: number of sub-centers """ def __init__(self, in_features, out_features, scale=32.0, margin=0.2, easy_margin=False, K=3): super(ArcMarginProduct_subcenter, self).__init__() self.in_features = in_features self.out_features = out_features self.scale = scale self.margin = margin # subcenter self.K = K # initial classifier self.weight = nn.Parameter( torch.FloatTensor(self.K * out_features, in_features)) nn.init.xavier_uniform_(self.weight) self.easy_margin = easy_margin self.cos_m = math.cos(margin) self.sin_m = math.sin(margin) self.th = math.cos(math.pi - margin) self.mm = math.sin(math.pi - margin) * margin self.mmm = 1.0 + math.cos( math.pi - margin) # this can make the output more continuous ######## self.m = self.margin ######## def update(self, margin=0.2): self.margin = margin self.cos_m = math.cos(margin) self.sin_m = math.sin(margin) self.th = math.cos(math.pi - margin) self.mm = math.sin(math.pi - margin) * margin self.m = self.margin self.mmm = 1.0 + math.cos(math.pi - margin) def forward(self, input, label): # 对cos(theta)的额外处理是与ArcFace的唯一区别 cosine = F.linear(F.normalize(input), F.normalize(self.weight)) # (batch, out_dim * k) cosine = torch.reshape( cosine, (-1, self.out_features, self.K)) # (batch, out_dim, k) # 取max是因为cos(theta)是相似度,与theta刚好成反比 # 如果现在处理的是theta,则应取min,然后取cos cosine, _ = torch.max(cosine, 2) # (batch, out_dim) sine = torch.sqrt(1.0 - torch.pow(cosine, 2)) phi = cosine * self.cos_m - sine * self.sin_m if self.easy_margin: phi = torch.where(cosine > 0, phi, cosine) else: ######## # phi = torch.where(cosine > self.th, phi, cosine - self.mm) phi = torch.where(cosine > self.th, phi, cosine - self.mmm) ######## one_hot = input.new_zeros(cosine.size()) one_hot.scatter_(1, label.view(-1, 1).long(), 1) output = (one_hot * phi) + ((1.0 - one_hot) * cosine) output *= self.scale return output def extra_repr(self): return 'in_features={}, out_features={}, scale={}, margin={}, ' \ 'easy_margin={}, K={}'.format( self.in_features, self.out_features, self.scale, self.margin, self.easy_margin, self.K)