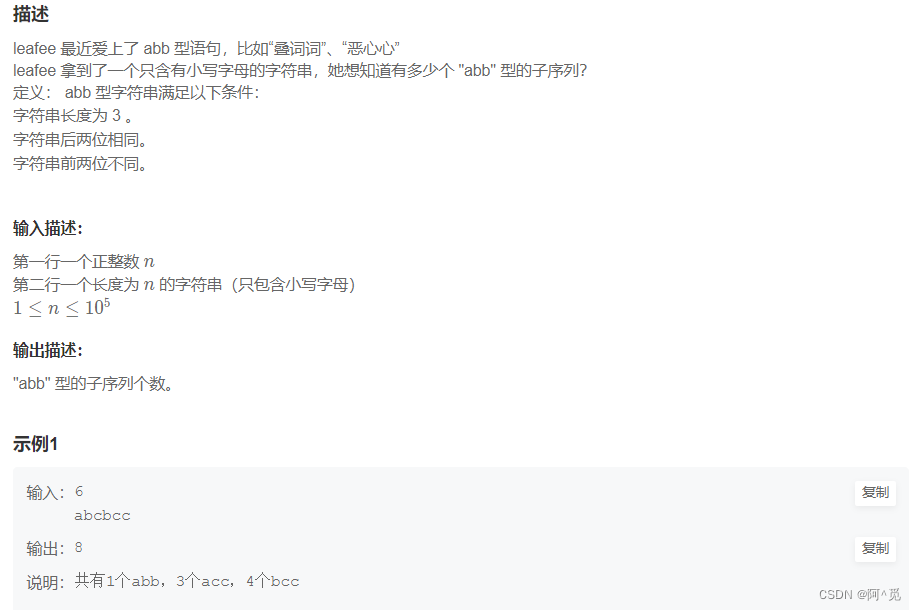
原理
ResNet 解决了什么问题?
一言以蔽之:解决了深度的神经网络难以训练的问题。
具体的说,理论上神经网络的深度越深,其训练效果应该越好,但实际上并非如此,层数越深会导致越差的结果并且容易产生梯度爆炸或梯度消失等问题。
ResNet 怎么解决的?
提出了一个残差学习网络的框架,该框架解决了上述问题。
残差网络的架构
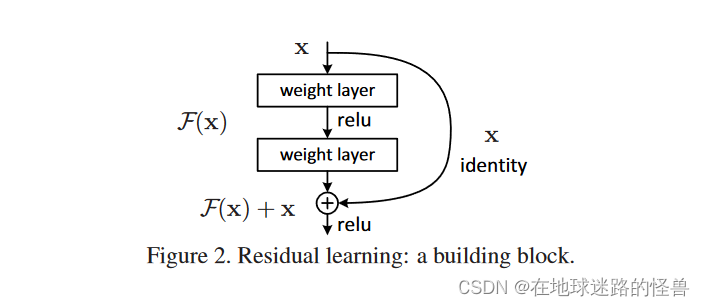
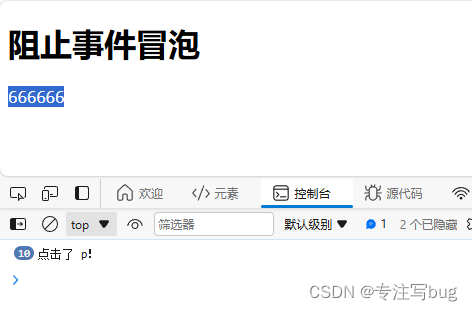
整个架构如上图所示。
首先我们要学习的东西是 H(x),假设现在已经有了一个浅的网络,然后我们要在上面新加一些层,让网络变得更深,如果按传统的做法那么新加的层就继续跟之前一样进行学习就行了。但是现在在新加的层中我们不直接去学 H(x),而是应该去学 H(x) - x。x 就是之前比较浅的网络已经学到的那个东西,也就是在新加的层中不去重新学个东西而只是学学到的东西和真实的东西二者之间的残差 H(x) - x,然后该层最后的输出结果 F(x) 再加上原始数据 x 就是最终结果也就是 F(x) + x ,此时优化的目标就不再是原始的 H(x),而是 H(x) - x 这个东西。
这就是 ResNet 的核心思想。
我感觉有一篇文章讲的很好,可以参考一下:ResNet网络详细讲解
下面是论文原文的描述:
在本文中,我们通过引入一个深度残差学习框架来解决退化问题。我们不希望每几个堆叠层直接拟合一个期望的底层映射,而是明确地让这些层拟合一个残差映射。在形式上,我们将期望的底层映射表示为H ( x ),并让堆叠的非线性层拟合F ( x )的另一个映射:= H ( x ) - x。原始映射被重铸成F ( x ) + x。我们假设优化残差映射比优化原始的、未引用的映射更容易。在极端情况下,如果一个恒等映射是最优的,那么将残差推到零比用一堆非线性层拟合一个恒等映射更容易。
F ( x ) + x的表达式可以通过具有"捷径连接"的前馈神经网络来实现(图2 )。快捷方式连接[ 2、33、48]是那些跳过一个或多个层的连接。在我们的例子中,快捷连接只是执行身份映射,它们的输出被添加到堆叠层的输出中(图2 )。身份捷径连接既不增加额外的参数,也不增加计算复杂度。整个网络仍然可以通过反向传播的SGD进行端到端的训练,并且可以很容易地使用公共库(例如, Caffe )实现,无需修改求解器。
我们在ImageNet [ 35 ]上进行了全面的实验来展示退化问题并评估我们的方法。研究表明:
1 )我们的深度残差网络易于优化,但对应的"普通"网络(简单地堆叠层)在深度增加时表现出更高的训练误差;
2 )我们的深度残差网络可以很容易地从大幅增加的深度中获得精度增益,产生的结果明显优于以前的网络。
在ImageNet分类数据集上[ 35 ],我们通过极深的残差网络获得了优异的结果。我们的152层残差网络是ImageNet上有史以来最深层的网络,但仍比VGG网络具有更低的复杂度[ 40 ]。我们的集成在ImageNet测试集上有3.57 %的top - 5误差,并在ILSVRC 2015分类竞赛中获得第一名。在其他识别任务上也具有出色的泛化性能,并引领我们在ILSVRC & COCO 2015竞赛中进一步获得第1名:ImageNet检测、ImageNet定位、COCO检测和COCO分割。这有力的证据表明,残差学习原理具有一般性,我们预期它在其他视觉和非视觉问题中也适用。
代码复现
这里给出我自己的模型代码:
import torch
from torch import nn
# 基本残差块
class BasicBlock(nn.Module):
expansion = 1
"""
参数解释:
in_ch:输入通道数
block_ch:输出通道数
stride:步长,通过该参数我们就可以实现网络结构中特征图Size减半、通道数增加一倍的效果
downSample:其本身也是一个网络,用来实现残差网络中的跳跃连接(也就是论文中虚线和实线)
同时跳跃连接也是用来区别基本残差块和瓶颈残差块的,二者区别如下:
基本残差块:输入输出通道数相同
瓶颈残差块:输入输出通道数不同,需要进行升维操作才能对位相加
另外二者的结构不同,可以通过论文看到
"""
def __init__(self, in_ch, block_ch, stride=1, downSample=None):
super().__init__()
self.downSample = downSample
# 从网络结构图中可以看到,先进行第一层卷积
self.conv1 = nn.Conv2d(in_ch, block_ch, kernel_size=3, stride=stride, padding=1, bias=False)
# 在网络模型中添加一个二维批归一化(Batch Normalization)层。
# 批归一化是一种用于加速神经网络训练并提高其性能的技术,类似于将上面所输出的数据进行了统一整理
self.bn1 = nn.BatchNorm2d(block_ch)
# 激活函数
self.relu1 = nn.ReLU()
# 第二层卷积
self.conv2 = nn.Conv2d(block_ch, block_ch * self.expansion, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(block_ch * self.expansion)
self.relu2 = nn.ReLU()
def forward(self, x):
identity = x
# 如果downSample参数不为空,说明其需要升维(也就是论文中虚线的样子)
if self.downSample is not None:
# 升维,让输入输出的通道数对齐
identity = self.downSample(x)
out = self.relu1(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
# 这里就是论文中的输出与原始输入进对位相加的步骤
out += identity
# 对位相加结束后再进行 relu 函数的激活,然后输出结果
return self.relu2(out)
# 瓶颈残差块
class Bottleneck(nn.Module):
# 从论文的网络结构图中不难发现,瓶颈残差块在第三层卷积时通道数会放大四倍
# 因此定义一个 expansion 变量
expansion = 4
"""
参数解释:
in_ch:输入通道数
block_ch:输出通道数
stride:步长,通过该参数我们就可以实现网络结构中特征图Size减半、通道数增加一倍的效果
downSample:其本身也是一个网络,用来实现残差网络中的跳跃连接(也就是论文中虚线和实线)
同时跳跃连接也是用来区别基本残差块和瓶颈残差块的,二者区别如下:
基本残差块:输入输出通道数相同
瓶颈残差块:输入输出通道数不同,需要进行升维操作才能对位相加
另外二者的结构不同,可以通过论文看到
"""
def __init__(self, in_ch, block_ch, stride=1, downSample=None):
super().__init__()
self.downSample = downSample
# 从网络结构图中可以看到,先进行第一层卷积
self.conv1 = nn.Conv2d(in_ch, block_ch, kernel_size=1, stride=stride, bias=False)
# 在网络模型中添加一个二维批归一化(Batch Normalization)层。
# 批归一化是一种用于加速神经网络训练并提高其性能的技术,类似于将上面所输出的数据进行了统一整理
self.bn1 = nn.BatchNorm2d(block_ch)
# 激活函数
self.relu1 = nn.ReLU()
# 第二层卷积
self.conv2 = nn.Conv2d(block_ch, block_ch, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(block_ch)
self.relu2 = nn.ReLU()
# 第三层卷积
self.conv3 = nn.Conv2d(block_ch, block_ch * self.expansion, kernel_size=1, stride=1, bias=False)
self.bn3 = nn.BatchNorm2d(block_ch * self.expansion)
self.relu3 = nn.ReLU()
def forward(self, x):
identity = x
# 如果downSample参数不为空,说明其需要升维(也就是论文中虚线的样子)
if self.downSample is not None:
# 升维,让输入输出的通道数对齐
identity = self.downSample(x)
out = self.relu1(self.bn1(self.conv1(x)))
out = self.relu2(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
# 这里就是论文中的输出与原始输入进对位相加的步骤
out += identity
# 对位相加结束后再进行 relu 函数的激活,然后输出结果
return self.relu3(out)
# 残差网络
class ResNet(nn.Module):
"""
in_ch: 默认为3,因为残差网络就是用来图片分类的,所以输入通道数默认为 3
num_classes:分类的数量,默认设置为100,即 100 种分类
block:用来区别是 基本残差块 还是 瓶颈残差块
block_num:每个残差块所需要堆叠的次数(也是论文中提供的有)
"""
def __init__(self, in_ch=3, num_classes=100, block=Bottleneck, block_num=[3, 4, 6, 3]):
super().__init__()
# 因为在各层之间通道数会发生变化,因此要进行跟踪
self.in_ch = in_ch
# 对于残差网络来说,不管是什么类型其一开始都要进行 7x7 的卷积和 3x3 的池化
# 因此我们直接照搬即可(论文中已经有了)
self.conv1 = nn.Conv2d(in_ch, 64, kernel_size=7, stride=2, padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.maxpool1 = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.in_ch = 64
# 将残差块堆叠起来,形成一个一个的残差层,进而构建成ResNet
self.layer1 = self._make_layer(block, 64, block_num[0], stride=1)
self.layer2 = self._make_layer(block, 128, block_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, block_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, block_num[3], stride=2)
# 最后是全连接层,做预测的
self.fc_layer = nn.Sequential(
nn.Linear(512*block.expansion*7*7, num_classes),
nn.Softmax(dim=-1)
)
def _make_layer(self, block, block_ch, block_num, stride=2):
layers = []
downSample = nn.Conv2d(self.in_ch, block_ch * block.expansion, kernel_size=1, stride=stride)
layers += [block(self.in_ch, block_ch, stride=stride, downSample=downSample)]
self.in_ch = block_ch * block.expansion
for _ in range(1, block_num):
layers += [block(self.in_ch, block_ch)]
return nn.Sequential(*layers)
def forward(self, x):
out = self.maxpool1(self.bn1(self.conv1(x))) #(1, 3, 224, 224) -> (1, 64, 56, 56)
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = out.reshape(out.shape[0], -1)
out = self.fc_layer(out)
return out
if __name__ == '__main__':
# 接下来进行测试
# 这行代码创建了一个形状为 (1, 3, 224, 224) 的四维张量 x,
# 其中包含了一个大小为 1 的批次中的一个 224x224 像素的 RGB 图像。
x = torch.randn(1, 3, 224, 224)
resnet = ResNet(in_ch=3, num_classes=100, block=Bottleneck, block_num=[2, 2, 2, 2])
y = resnet(x)
print(y.shape)