目录
1.提取不重复的整数
2.【模板】哈夫曼编码
3.abb
1.提取不重复的整数
链接![]() https://www.nowcoder.com/practice/253986e66d114d378ae8de2e6c4577c1?tpId=37&tqId=21232&ru=/exam/oj
https://www.nowcoder.com/practice/253986e66d114d378ae8de2e6c4577c1?tpId=37&tqId=21232&ru=/exam/oj
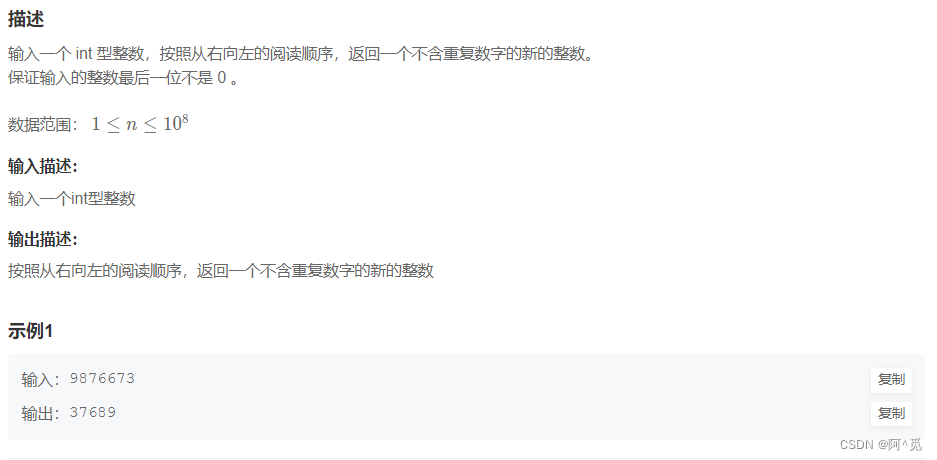
按照题意模拟就行,记得从右往左遍历
#include <iostream>
using namespace std;
int a[10];
int main() {
string s;
cin >> s;
for (int i = s.size() - 1; i >= 0; --i)
if (a[s[i] - '0']++ == 0)
cout << s[i] - '0';
cout << endl;
return 0;
}2.【模板】哈夫曼编码
链接![]() https://www.nowcoder.com/practice/4c0419eb07c840ca8402e4f2a52cfd49?tpId=308&tqId=40489&ru=/exam/oj
https://www.nowcoder.com/practice/4c0419eb07c840ca8402e4f2a52cfd49?tpId=308&tqId=40489&ru=/exam/oj

做这题前首先需要去了解哈夫曼编码。
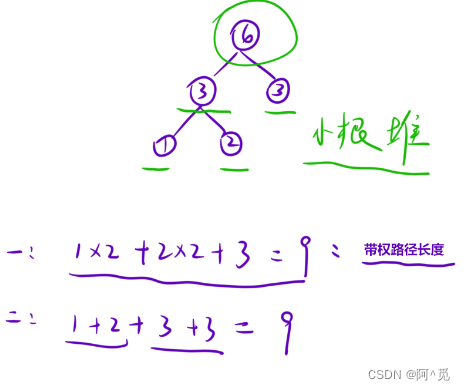

因为题中已经给出了每个字符的频次,因此可以直接用优先队列(堆)解决,但别忘了用小根堆。
3.abb
链接![]() https://www.nowcoder.com/practice/0a8bbf8b9b5b4280957849ef4f240f07?tpId=230&tqId=38957&ru=/exam/oj
https://www.nowcoder.com/practice/0a8bbf8b9b5b4280957849ef4f240f07?tpId=230&tqId=38957&ru=/exam/oj
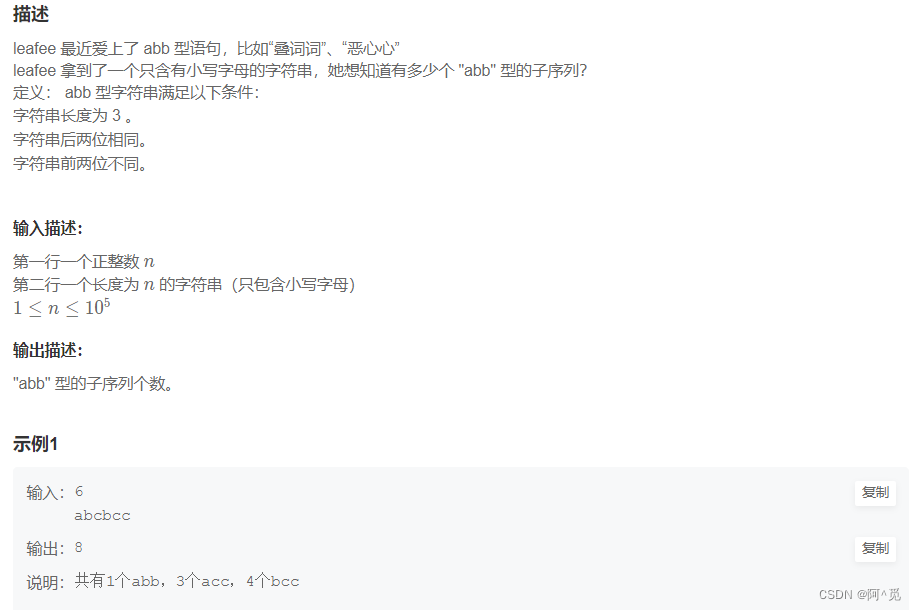
一道动态规划题,同样是去找出它的状态表示:
dp[x] : 以 x 元素结尾的所有子序列中,_xx的个数。
要想拿到dp[x],则需要找到以 x 元素结尾的所有子序列中,_x的个数。
将其(以 x 元素结尾的所有子序列中,_x的个数)定义为 f[x] ,要想拿到 f[x] ,则需要找到区间[0, i - 1]中非 x 的个数,(这里我们转化为 x 的个数,最后用 i {区间总数} 减去 x 个数即可),(定义为g[x])。
然后就是状态转移方程:
dp[x] = f[x], (因为这时候遍历到的数就是 x, _x 加上x即为_xx)
f[x] = f[x] + (i - g[x])
g[x] = g[x] + 1
注意状态转移方程顺序,要先更新 f[x] 后才能更新 g[x]。
最后是返回值:
返回的是所有字母为结尾的个数的和。即所有的dp[x]。因为dp[x] = f[x]。
所以可以不需要dp[x]。
#include <iostream>
#define int long long
using namespace std;
int f[26];
int g[26];
char s[100010];
int n;
signed main() {
cin >> n;
for(int i = 0; i < n; ++i)
cin >> s[i];
int ret = 0;
for(int i = 0; i < n; ++i)
{
int x = s[i] - 'a';
ret += f[x];
f[x] = f[x] + i - g[x];
g[x] = g[x] + 1;
}
cout << ret << endl;
return 0;
}