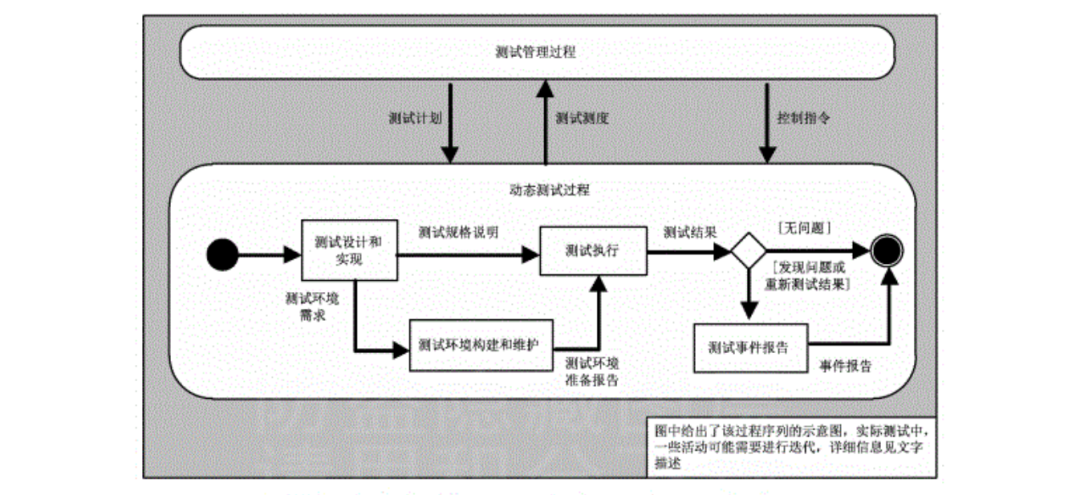
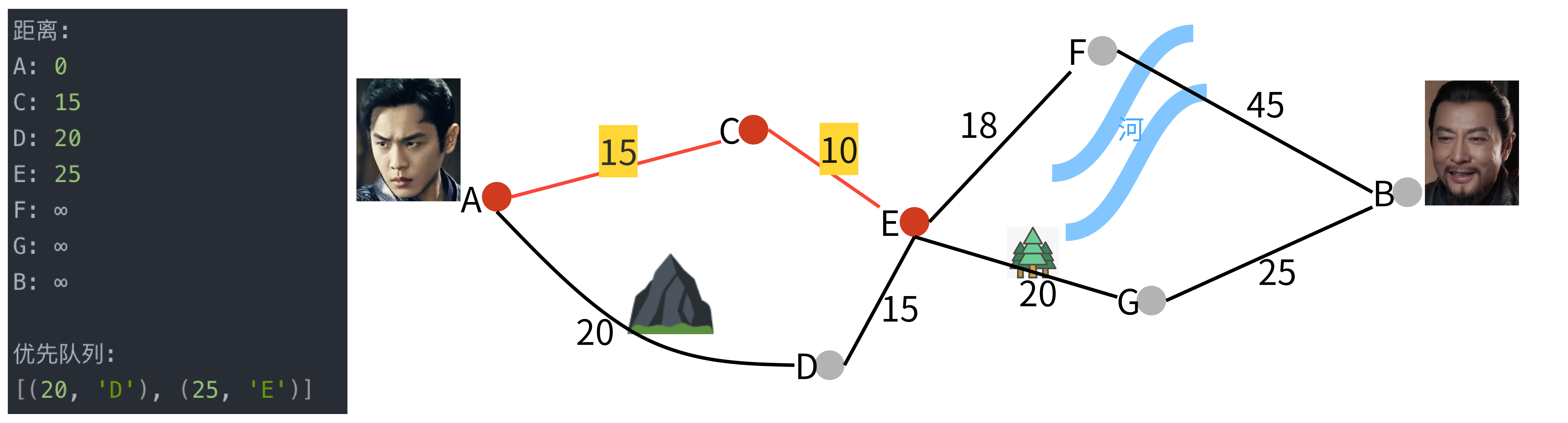
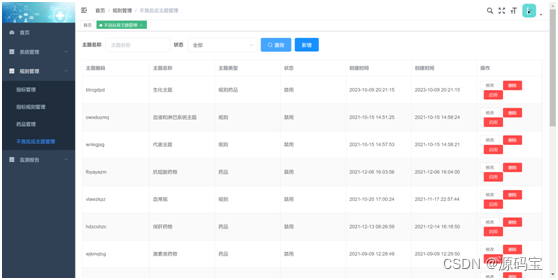
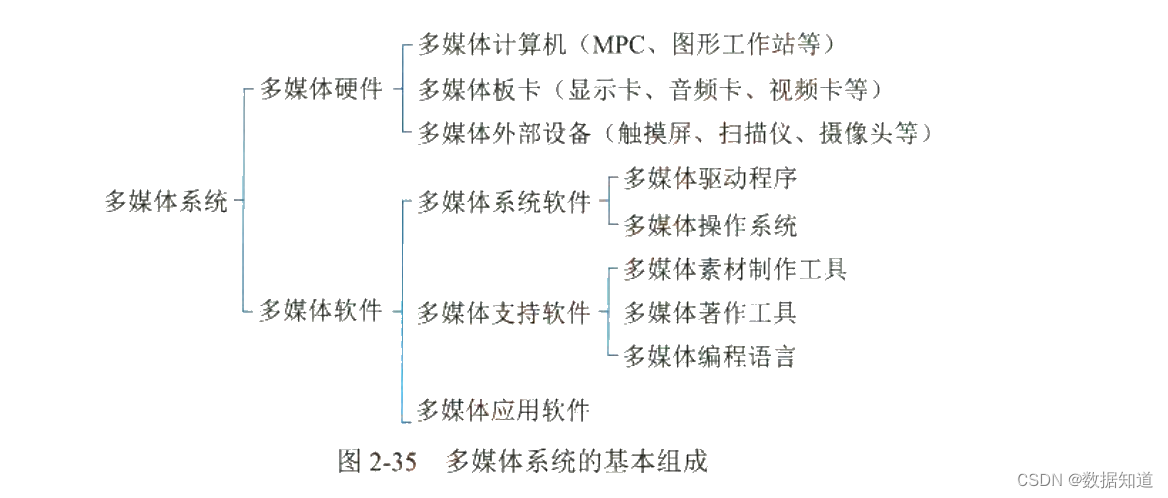
模拟集成电路(5)----单级放大器（共栅级）
有一些场合需要一些小的输入电阻（电流放大器）
大信号分析
− W h e n V i n ≥ V B − V T H ∙ M 1 i s o f f , V o u t = V D D − F o r L o w e r V i n I d = 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 V o u t = V D D − 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 ⋅ R D \begin{aligned} &-\mathrm{~When~}V_{in}\geq V_B-V_{TH} \\ &\bullet\mathrm{M}_1\mathrm{~is~off},V_{out}=V_{DD} \\ &-\mathrm{~For~Lower~}V_{in} \\ &I_{d}=\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2} \\ &V_{out}=V_{DD}-\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2}\cdot R_{D} \end{aligned} − When Vin≥VB−VTH∙M1 is off,Vout=VDD− For Lower VinId=21μnCoxLW(VB−Vin−VTH)2Vout=VDD−21μnCoxLW(VB−Vin−VTH)2⋅RD
− When V i n < V i n 1 , M 1 enters triode region V D D − 1 2 μ n C o x W L ( V B − V i n 1 − V T H ) 2 ⋅ R D = V B − V T H \begin{aligned}&-\text{ When }V_{in}<V_{in1},\text{M}_1\text{ enters triode region}\\&V_{DD}-\frac12\mu_nC_{ox}\frac{W}L(V_B-V_{in1}-V_{TH})^2\cdot R_D=V_B-V_{TH}\end{aligned} − When Vin<Vin1,M1 enters triode regionVDD−21μnCoxLW(VB−Vin1−VTH)2⋅RD=VB−VTH
大信号特性图
求增益
V o u t = V D D − 1 2 μ n C o x W L ( V B − V i n − V T H ) 2 R D ∂ V o u t ∂ V i n = − μ n C o x W L ( V B − V i n − V T H ) ( − 1 − ∂ V T H ∂ V i n ) R D \begin{aligned}&V_{out}=V_{DD}-\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})^{2}R_{D}\\&\frac{\partial V_{out}}{\partial V_{in}}=-\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})(-1-\frac{\partial V_{TH}}{\partial V_{in}})R_{D}\end{aligned} Vout=VDD−21μnCoxLW(VB−Vin−VTH)2RD∂Vin∂Vout=−μnCoxLW(VB−Vin−VTH)(−1−∂Vin∂VTH)RD
∵ ∂ V T H / ∂ V i n = ∂ V T H / ∂ V S B = η , A ν = ∂ V o u t ∂ V i n = μ n C o x W L ( V B − V i n − V T H ) ( 1 + η ) R D \because\quad\partial V_{TH}/\partial V_{in}=\partial V_{TH}/\partial V_{SB}=\eta,\\A_{\nu}=\frac{\partial V_{out}}{\partial V_{in}}=\mu_{n}C_{ox}\frac{W}{L}(V_{B}-V_{in}-V_{TH})(1+\eta)R_{D} ∵∂VTH/∂Vin=∂VTH/∂VSB=η,Aν=∂Vin∂Vout=μnCoxLW(VB−Vin−VTH)(1+η)RD
A ν = g m ( 1 + η ) R D A_\nu=g_m(1+\eta)R_D Aν=gm(1+η)RD
小信号分析
ν
b
s
=
−
ν
i
n
ν
1
=
−
ν
i
n
\nu_{bs}=-\nu_{in}\quad\nu_{1}=-\nu_{in}
νbs=−νinν1=−νin
ν o u t = − [ g m ν 1 + g m b ν b s + ( ν o u t − ν i n ) / r o ] ⋅ R D \nu_{out}=-[g_{m}\nu_{1}+g_{mb}\nu_{bs}+(\nu_{out}-\nu_{in})/r_{o}]\cdot R_{D} νout=−[gmν1+gmbνbs+(νout−νin)/ro]⋅RD
A ν = ν o u t ν i n = g m + g m b + 1 / r o 1 + R D / r o ⋅ R D ≈ ( g m + g m b ) ⋅ R D A_{\nu}=\frac{\nu_{out}}{\nu_{in}}=\frac{g_{m}+g_{mb}+1/r_{o}}{1+R_{D}/r_{o}}\cdot R_{D}\approx(g_{m}+g_{mb})\cdot R_{D} Aν=νinνout=1+RD/rogm+gmb+1/ro⋅RD≈(gm+gmb)⋅RD
如果输入电流源有无限的阻抗
R
s
R_s
Rs
ν
1
=
−
[
ν
i
n
−
(
ν
o
u
t
/
R
D
)
⋅
R
S
)
ν
b
s
=
ν
1
\nu_1=-[\nu_{in}-(\nu_{out}/R_D)\cdot R_S)\quad\nu_{bs}=\nu_1
ν1=−[νin−(νout/RD)⋅RS)νbs=ν1
ν o u t = − [ g m ν 1 + ( ν o u t + ν 1 ) / r o + g m b ν b s ] ⋅ R D A ν = ν o u t ν i n = g m + g m b + 1 / r o 1 + ( g m + g m b ) R S + ( R D + R S ) / r o ⋅ R D \nu_{out}=-[g_{m}\nu_{1}+(\nu_{out}+\nu_{1})/r_{o}+g_{mb}\nu_{bs}]\cdot R_{D}\\A_{\nu}=\frac{\nu_{out}}{\nu_{in}}=\frac{g_{m}+g_{mb}+1/r_{o}}{1+(g_{m}+g_{mb})R_{S}+(R_{D}+R_{S})/r_{o}}\cdot R_{D} νout=−[gmν1+(νout+ν1)/ro+gmbνbs]⋅RDAν=νinνout=1+(gm+gmb)RS+(RD+RS)/rogm+gmb+1/ro⋅RD
CG的输入电阻
ν 1 = − ν x ν b s = − ν x \nu_1=-\nu_x\quad\nu_{bs}=-\nu_x ν1=−νxνbs=−νx
i x R D + r o ( i x − ( g m + g m b ) ν x = ν x i_{x}R_{D}+r_{o}(i_{x}-(g_{m}+g_{mb})\nu_{x}=\nu_{x} ixRD+ro(ix−(gm+gmb)νx=νx
r i n = ν x i x = R D / r o + 1 1 / r o + ( g m + g m b ) ≈ 1 g m + g m b r_{in}=\frac{\nu_{x}}{i_{x}}=\frac{R_{D}/r_{o}+1}{1/r_{o}+(g_{m}+g_{mb})}\approx\frac{1}{g_{m}+g_{mb}} rin=ixνx=1/ro+(gm+gmb)RD/ro+1≈gm+gmb1
R D R_D RD的影响
r i n = ν x i x = R D / r o + 1 1 / r o + ( g m + g m b ) r_{in}=\frac{\nu_{x}}{i_{x}}=\frac{R_{D}/r_{o}+1}{1/r_{o}+(g_{m}+g_{mb})} rin=ixνx=1/ro+(gm+gmb)RD/ro+1
输出电阻
$$ \begin{aligned}r_{out}&=r_{OD}\left\|R_{D}\right\|\\&=\{r_{O}+[1+(g_{m}+g_{mb})r_{O}]\cdot R_{S}\}\|R_{D}\end{aligned} $$
− i f R s = 0 ⟶ r o u t = r O ∥ R D ∥ \begin{array}{cc}{-\mathrm{if}R_{s}=0}\\\\{\longrightarrow}&{r_{out}=r_{O}\left\|R_{D}\right\|}\\\end{array} −ifRs=0⟶rout=rO∥RD∥
