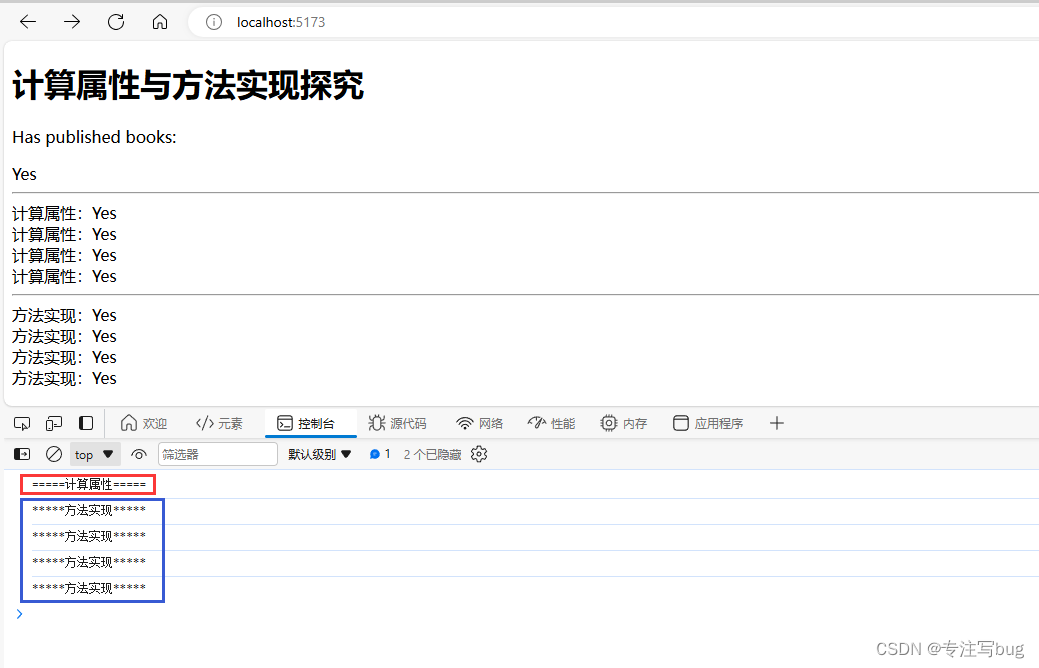
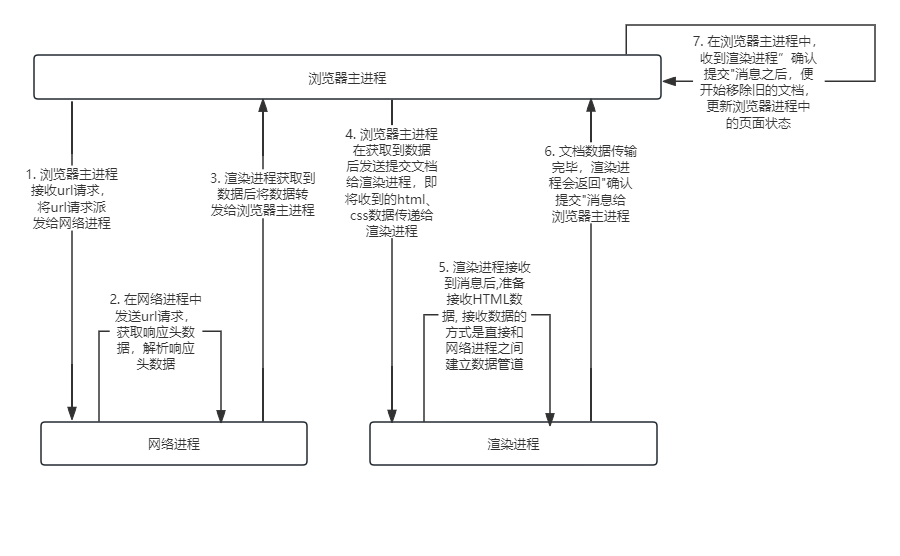
一、问题描述

二、解题思路

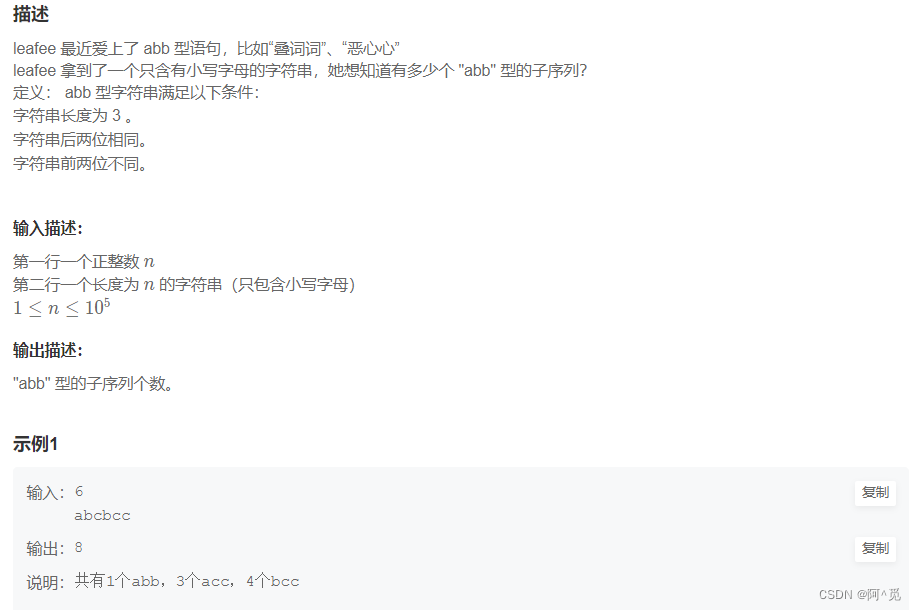
这个题目其实是求给出数组中，子数组和不大于M中，和最大值的子数组。

求子数组使用双指针就可以解决问题，相对比较简单。（如果是子序列，则等价于0-1背包问题，看题目扩展中的问题）

三、代码实现

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param trees int整型一维数组 
     * @param M int整型 
     * @return int整型
     */
    public int maxFruits (int[] trees, int M) {
        // 题目要求的是trees中不超过M的最大子数组的和
        int maxnum=0;
        for(int i=0;i<trees.length;i++){
            for(int j=i;j<trees.length;j++){
                int nowsum=arrSum(trees,i,j);
                if(nowsum<M){
                    maxnum=maxnum>nowsum?maxnum:nowsum;
                }else if(nowsum==M){
                    maxnum=M;
                }else{
                    //当前子数组超过最大值M，不做任何处理
                }
            }
        }
        return maxnum;
    }
    public int arrSum(int []trees,int i,int j){
        int sum=0;
        for(;i<=j;i++){
            sum+=trees[i];
        }
        return sum;
    }
}

四、刷题链接

牛牛的果实收集_牛客题霸_牛客网

五、题目扩展（动态规划：0-1背包问题）

(1)分析过程

(2)代码实现

import java.util.Arrays;

public class BegProblem {
    public static int getMaxValue(int[] arr,int[] values,int volumn){
        
        //初始化dp数组
        int[][] dpArr=new int[arr.length+1][volumn+1];
        for(int i=1;i<volumn+1;i++){
            //初始化第一行：arr[0]和当前容量对比
            dpArr[1][i]=arr[0]<=i?values[0]:0;
        }

        for(int i=1;i<arr.length+1;i++){
            //初始化第一列：
            dpArr[i][1]=arr[i-1]==1?values[i-1]:0;
        }

        //动态规划
        for(int i=2;i<=arr.length;i++){
            for(int j=2;j<=volumn;j++){
                //状态转移方程
                int nowvolumn=arr[i-1];
                int nowvalue=values[i-1];
                if(nowvolumn<j){
                    dpArr[i][j]=Math.max(dpArr[i-1][j],dpArr[i][j-nowvolumn]+nowvalue);
                }else{
                    dpArr[i][j]=dpArr[i-1][j];
                }
            }
        }
        
        //打印一下dp数组(二维)
        for(int i=0;i<arr.length+1;i++){
            String s1=Arrays.toString(dpArr[i]);
            System.out.println(s1);
        }

        return dpArr[arr.length][volumn];
    }

    public static void main(String[] args) {
        //测试用例：
        int[] arr={1,2,3,4,5};
        int[] values={2,4,4,5,6};

        int maxvalue=getMaxValue(arr,values,6);
        System.out.println("最大值:"+maxvalue);
        
    }
}

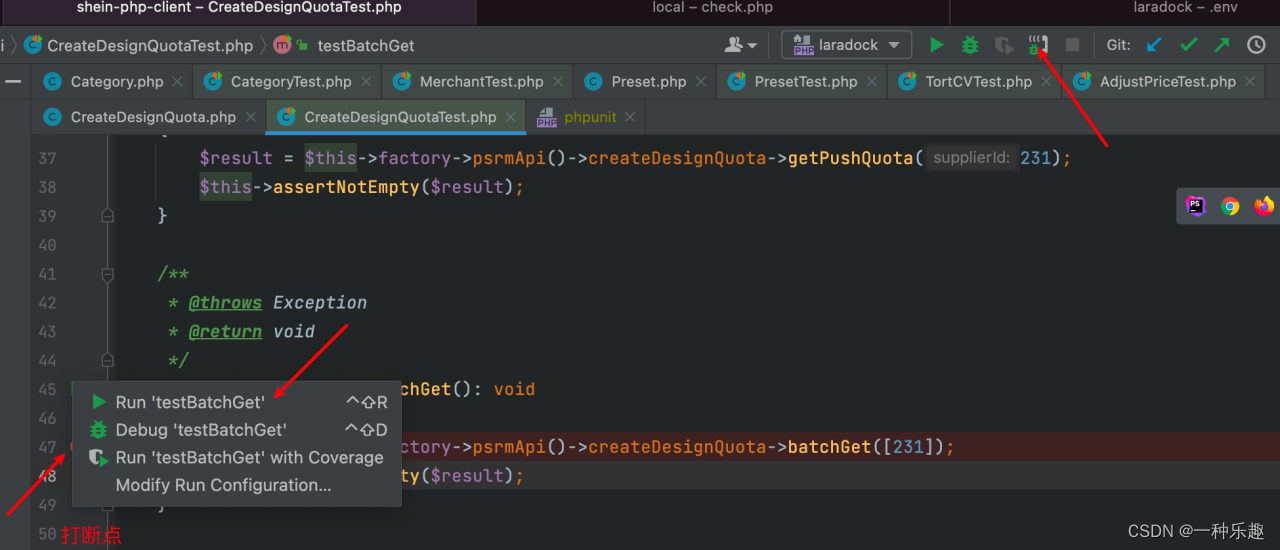
(3)执行效果