栈和队列专题（LeetCode）

news2024/11/17 1:30:40

目录

  • 有效的括号
    • 题解
    • 代码加解释
  • 用队列实现栈
    • 题解
    • 代码加解释
  • 设计循环队列
    • 题解
    • 代码加解释
  • 用栈实现队列
    • 题解
    • 代码加解释

有效的括号

在这里插入图片描述

题解

左括号从s字符串中取出来放入栈中
s中就只有右括号了
那么栈顶的左括号和s的右括号匹配即可
代码中也详细解释了左括号和右括号多少的问题

代码加解释

bool isValid(char* s) 
{
    Stack sl;
    StackInit(&sl);
    while(*s)
    {
        //先插入左括号
        if(*s == '('||
           *s == '{'||
           *s == '[')
           {
             StackPush(&sl,*s);
           }
        else//右括号取栈顶左括号尝试匹配
        {
           if(STEmpty(&sl))
           {
            //解决右括号比左括号多的情况
            //s中只有右括号，top == 0
            StackDestroy(&sl);
            //释放sl指向的空间
            return false;
           }
           //取栈顶数据
           char top = STTop(&sl);
           //把栈顶的括号取出来和右括号匹配
           StackPop(&sl);
           //弹出栈顶数据，方便取下一个数据
           //不匹配
           if(top == '('&& *s != ')'||
              top == '['&&*s != ']'||
              top == '{'&&*s != '}')
              {
                StackDestroy(&sl);
                return false;
              }
        }
        s++;
    }
    
    //栈不为空，左括号的数量比右括号的数量多，数量不匹配
    //只有一个左括号,假
    //解决的是右括号和左括号一样多和左括号多的情况
    bool ret = STEmpty(&sl);
    //栈为空，top == 0，真
    StackDestroy(&sl);
    return ret; 
}

用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

1 <= x <= 9
最多调用100 次 push、pop、top 和 empty
每次调用 pop 和 top 都保证栈不为空

进阶：你能否仅用一个队列来实现栈。

题解

实现各个接口，用两个队列实现栈
主体思路还是保证一个队列是空的，一个队列是非空的
空的队列用于导数据，比如非空队列 1 2 3 4,1 2 3导到空的队列中，4直接pop,对应栈顶的删除
非空的队列直接插入数据，因为队列是尾插，也就是栈顶的插入
在这里插入图片描述
MyStack下有一个重要的说明
1.后取地址，相当于开了一个新的队列，在新的队列中许多值是未定义的，相当于随机值，所以不能后取地址
在这里插入图片描述

2.先取地址，是对原队列进行操作，指针指向原队列
在这里插入图片描述

代码加解释

//C语言要造轮子，前面的接口在上一个博客，需要的可以自取
typedef struct 
{
  Queue q;//队列1
  Queue p;//队列2
} MyStack;

MyStack* myStackCreate() 
{
    //一个队列为空，另一个队列为有数据
    //把数据插入非空队列中，空的队列用来导数据
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    //不能和题里创建一样的指针，重定义
    QueueInit(&(obj->p));
    QueueInit(&(obj->q));
    //初始化队列1和队列2

    return obj;
}

void myStackPush(MyStack* obj, int x) 
{
    if(!QueueEmpty(&(obj->p)))
    {
        QueuePush(&(obj->p),x);
        //第一个队列是非空的就插入第一个队列中
    }   
    else//1.p空q非空，插入队列q 2.p空q空，这种随便插入那个队列
    {
        QueuePush(&(obj->q),x);
    }
}

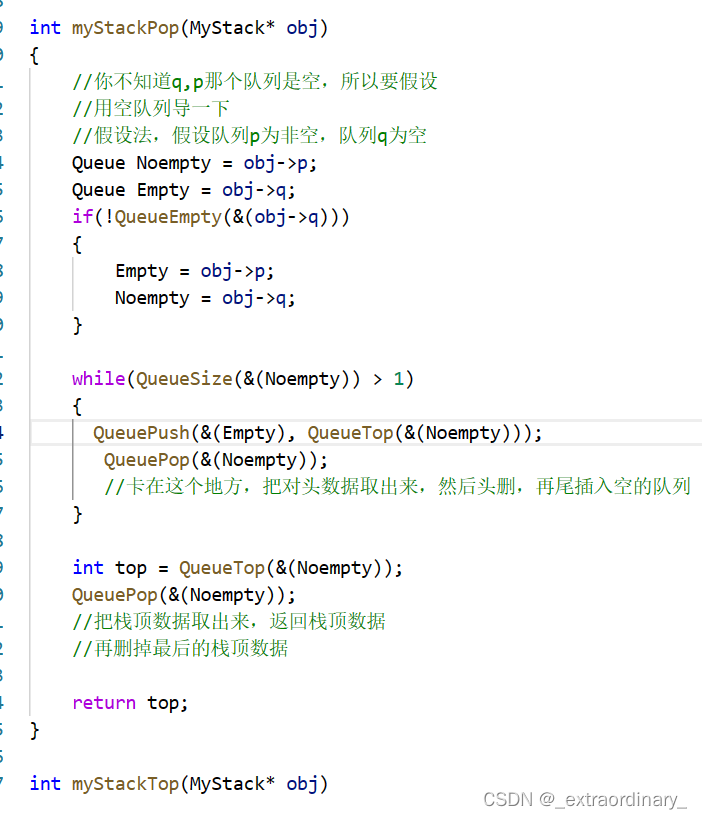
int myStackPop(MyStack* obj) 
{
    //你不知道q,p那个队列是空，所以要假设
    //用空队列导一下
    //假设法，假设队列p为非空，队列q为空
    Queue* Noempty = &(obj->p);
    Queue* Empty = &(obj->q);
    if(!QueueEmpty(&(obj->q)))
    {
        Empty = &(obj->p);
        Noempty = &(obj->q);
    }   
    
    while(QueueSize(Noempty) > 1)
    {
      QueuePush(Empty, QueueTop(Noempty));
       QueuePop(Noempty);
       //卡在这个地方，把对头数据取出来，然后头删，再尾插入空的队列
    }
    
    int top = QueueTop(Noempty);
    QueuePop(Noempty); 
    //把栈顶数据取出来，返回栈顶数据
    //再删掉最后的栈顶数据    

    return top;
}

int myStackTop(MyStack* obj) 
{
    if(!QueueEmpty(&(obj->q)))
    {
        return QueueTail(&(obj->q));
    }  
    else
    {
        return QueueTail(&(obj->p));
    }
}

bool myStackEmpty(MyStack* obj) 
{
   return QueueEmpty(&(obj->q)) && QueueEmpty(&(obj->p));    
}

void myStackFree(MyStack* obj) 
{
   QueueDestroy(&(obj->q));
   QueueDestroy(&(obj->p));

   free(obj);    
}

/**  * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
  * myStackPush(obj, x);
 
  * int param_2 = myStackPop(obj);
 
  * int param_3 = myStackTop(obj);
 
  * bool param_4 = myStackEmpty(obj);
 
  * myStackFree(obj);
 */

设计循环队列

在这里插入图片描述

题解

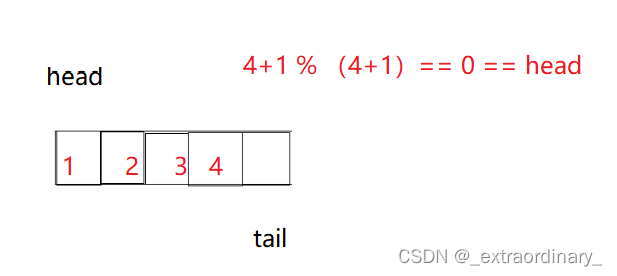
主要多开一个空间为了解决假溢出问题
代码里也有写

队列为空 -> head == tail
在这里插入图片描述

队列为满 -> （tail+1）% （k+1） == head
%k+1 为了解决回绕问题
普通的情况tail + 1 = head
在这里插入图片描述

  • 插入数据 -> (obj->tail) %= (obj->k+1);
    tail++ 变成5又要解决回绕问题，%k+1回到0位置可以插入数据
  • 删除数据 -> obj->head %= (obj->k+1)
    head++ 变成5又要解决回绕问题，%k+1回到0位置可以删除数据
  • 取队头数据 -> obj->a[obj->head]
    head指向头直接取队头数据
  • 取队尾数据 ->
    1.return obj->a[(obj->tail-1 + obj->k+1) % (obj->k+1)]
    2.return obj->tail == 0 ? obj->a[obj->k] : obj->a[obj->tail-1]

tail是指向队尾的下一个位置
取队尾数据要tail - 1，但是tail == 0时，tail - 1就会越界，
tail == 0时要回绕到 tail == k 是队尾数据的下标

有两种方法可以理解第二种比较好理解
第一种取一个数据也比较好理解
比如tail = 0,k = 4 时，-1+5 = 4 % k+1 = 4,就取到队尾的下标了

代码加解释

typedef struct 
{
  int* a;
  int head;//指向头
  int tail;//指向尾
  int k;     
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) 
{
    
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    //多开一个空间，为了解决循环队列的假溢出问题
    //假溢出问题：比如开四个空间，head == tail是空，head == tail也是满
    obj->head = 0;
    obj->tail = 0;    
    obj->k = k;

    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->head == obj->tail;    
}

bool myCircularQueueIsFull(MyCircularQueue* obj)  
{
    // tail + 1 == head;
    return (obj->tail+1) % (obj->k+1) == obj->head;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }

    obj->a[obj->tail] = value;
    obj->tail++;
    (obj->tail) %= (obj->k+1);

    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }    

    obj->head++;
    obj->head %= (obj->k+1);

    return true;
}

int myCircularQueueFront(MyCircularQueue* obj)
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    
    return obj->a[obj->head];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    
    return obj->a[(obj->tail-1 + obj->k+1) % (obj->k+1)];
    //return obj->tail == 0 ? obj->a[obj->k] : obj->a[obj->tail-1];
}

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    //先把数组释放，再把结构体释放
    free(obj);
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/

用栈实现队列

在这里插入图片描述

题解

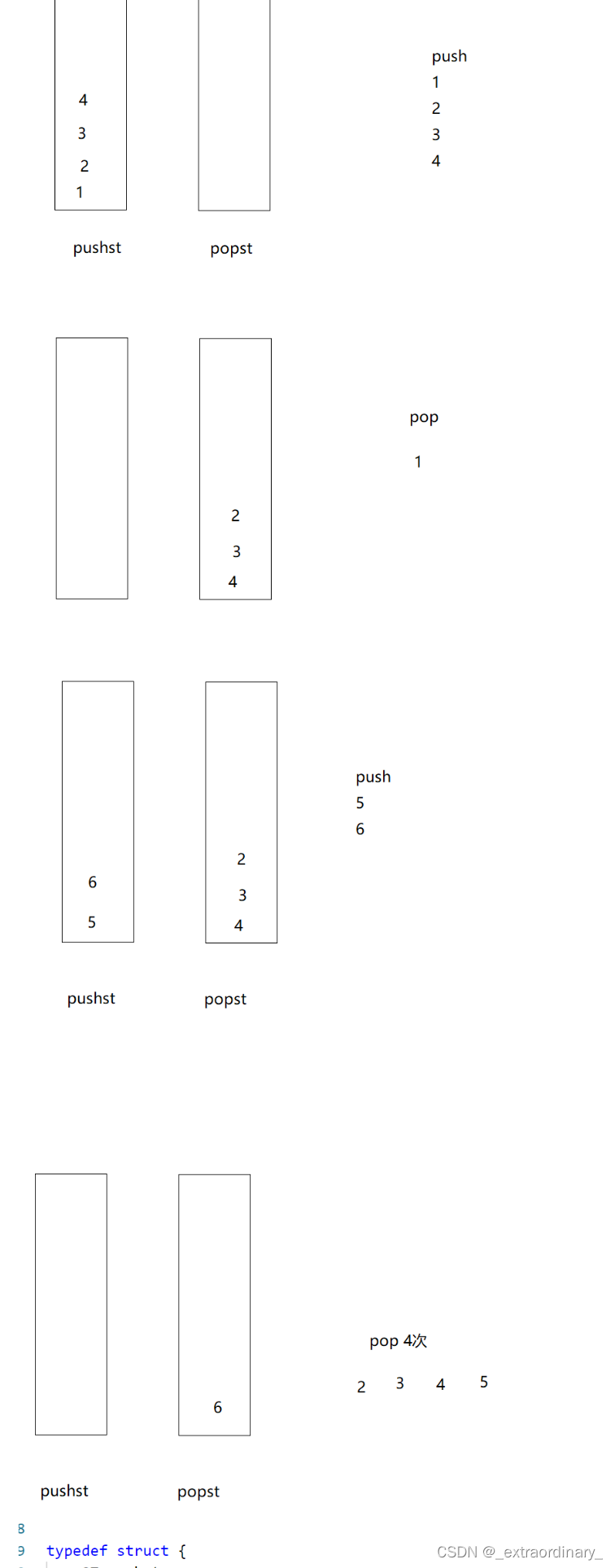
设计一个为poplist的栈和pushlist的栈
一个栈专门插入数据
一个栈专门删除数据
StackPush(&(obj->pushlist),x)
直接入栈达到了先进的效果
将pushlist中的数据导入poplist中，先进的数据就达到先出的效果了
poplist中有数据直接出
没有数据从pushlist中导数据在出数据
所以两个栈只要有一个栈是非空的就可以出数据
只要有一个栈是非空的，就是非空队列
在这里插入图片描述

代码加解释

typedef struct 
{
   Stack pushlist;
   Stack poplist;
   //后进先出栈实现先进先出队列
} MyQueue;


MyQueue* myQueueCreate() 
{
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&(obj->pushlist));
    StackInit(&(obj->poplist));

    return obj;
}

void myQueuePush(MyQueue* obj, int x) 
{
    //直接插入pushlist的队列，队尾入数据也就是栈顶入数据
    StackPush(&(obj->pushlist),x);
}

int myQueuePop(MyQueue* obj) 
{
   int front = myQueuePeek(obj);
   //push pop
   //传过去的应该是obj，指向两个栈的结构体指针
   StackPop(&(obj->poplist));
   return front;
}

int myQueuePeek(MyQueue* obj) 
{
    if(STEmpty(&(obj->poplist)))
    {
        while(!STEmpty(&(obj->pushlist)))
        {
            StackPush(&(obj->poplist),STTop(&(obj->pushlist)));
            StackPop(&(obj->pushlist));
        }
    }
    int ret = STTop(&(obj->poplist));

    return ret;
}

bool myQueueEmpty(MyQueue* obj) 
{
    return STEmpty(&(obj->pushlist)) && STEmpty(&(obj->poplist));    
}

void myQueueFree(MyQueue* obj) 
{
    StackDestroy(&(obj->pushlist));
    StackDestroy(&(obj->poplist));

    free(obj);
}

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1711201.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何成为快手外卖代理？本地生活服务平台加盟条件解析

如何成为快手外卖代理？本地生活服务平台加盟条件解析

近年来&#xff0c;以抖音、快手和小红书等为代表的互联网大厂纷纷进军本地生活领域&#xff0c;改变美团和饿了么二分天下的这一局面的同时&#xff0c;也让本地生活成为了众多创业者眼中的“香饽饽”。其中&#xff0c;快手凭借着其庞大的用户群体&#xff0c;让快手团购外卖…
阅读更多...
关于本人VIP付费文章说明

关于本人VIP付费文章说明

郑重声明&#xff1a;我写博客只是为了记录分享经验 自从上次写完数据结构系列后我就一直没有登陆&#xff0c;目前也没打算继续开新内容。今天偶然发现我之前写的文章被设为vip文章&#xff0c;要vip解锁才能看&#xff0c;我很确定当初我发布的时候选择的是公开&#xff0c;…
阅读更多...
LeetCode 474.一和零

LeetCode 474.一和零

没做出来&#xff0c;最后看了解析&#xff0c;看了半天才懂。 我一开始把这个题当成多重背包来做了&#xff0c;因为有0和1两个参数需要考虑&#xff0c;但是中间很多情况不知道怎么处理。后面看了解析才知道这是个01背包问题&#xff0c;0和1都是一个物品上的属性&#xff0c…
阅读更多...
HTML静态网页成品作业(HTML+CSS)——游戏阴阳师介绍网页(4个页面)

HTML静态网页成品作业(HTML+CSS)——游戏阴阳师介绍网页(4个页面)

&#x1f389;不定期分享源码&#xff0c;关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 &#x1f3f7;️本套采用HTMLCSS&#xff0c;未使用Javacsript代码&#xff0c;共有4个页面。 二、作品演示 三、代…
阅读更多...
RDP方式连接服务器上传文件方法

RDP方式连接服务器上传文件方法

随笔 目录 1. RDP 连接服务器 2. 为避免rdp 访问界面文字不清晰 3. 本地上传文件到服务器 1. RDP 连接服务器 # mstsc 连接服务器step1: 输入mstscstep2: 输入 IP, username, passwd 2. 为避免rdp 访问界面文字不清晰 解决方法&#xff1a; 3. 本地上传文件到服务器 step…
阅读更多...
《KAN》论文笔记

《KAN》论文笔记

原文出处 KAN: Kolmogorov–Arnold Networks (arxiv.org)https://arxiv.org/html/2404.19756v1 论文笔记 What 《KAN: Kolmogorov–Arnold Networks》——我们提出了 KolmogorovArnold Networks (KANs) 作为多层感知器 (MLP) 的有前途的替代方案。 我们表明&#xff0c;这…
阅读更多...
小程序自动化辅助渗透脚本（2024）

小程序自动化辅助渗透脚本（2024）

简介 1.还在一个个反编译小程序吗&#xff1f; 2.还在自己一个个注入hook吗&#xff1f; 3.还在一个个查看找接口、查找泄露吗&#xff1f; 现在有自动化辅助渗透脚本了&#xff0c;自动化辅助反编译、自动化注入hook、自动化查看泄露 注&#xff1a;本工具仅用于学习交流&…
阅读更多...
数据库系统概论（个人笔记）（第三部分）

数据库系统概论（个人笔记）（第三部分）

数据库系统概论&#xff08;个人笔记&#xff09; 文章目录 数据库系统概论&#xff08;个人笔记&#xff09;3、SQL介绍3.1 SQL查询语言概述3.2 SQL数据定义3.3 SQL查询的基本查询结构3.4 其他基本操作3.5 设置操作3.6 空值3.7 聚合函数3.8 嵌套子查询3.9 数据库的修改 3、SQL…
阅读更多...
VSCODE常用插件记录

VSCODE常用插件记录

重点提名&#xff1a; back & ForthBookmarksC/ChighlightSSH FS //SSH插件
阅读更多...
SQL2017附加从其他电脑复制过来的mdf数据后出现【只读】无法写入数据

SQL2017附加从其他电脑复制过来的mdf数据后出现【只读】无法写入数据

1. 尝试给它所在的文件夹的属性中的“只读”去勾&#xff0c;无果。 2. 其他文章提示是文件的问题。 该错误为文件权限错误&#xff0c;找到该数据库的 数据库文件 和 日志文件&#xff0c;在安全中添加 Authenticated Users 用户的权限&#xff0c;并设置 “完全控制”
阅读更多...
Linux：进程控制（二.详细讲解进程程序替换）

Linux：进程控制（二.详细讲解进程程序替换）

上次讲了&#xff1a;Linux&#xff1a;进程地址空间、进程控制&#xff08;一.进程创建、进程终止、进程等待&#xff09; 文章目录 1.进程程序替换1.1概念1.2原理1.3使用一个exec 系列函数execl&#xff08;&#xff09;函数结论与细节 2.多进程时的程序替换3.其他几个exec系…
阅读更多...
【链表】Leetcode 82. 删除排序链表中的重复元素 II【中等】

【链表】Leetcode 82. 删除排序链表中的重复元素 II【中等】

删除排序链表中的重复元素 II 给定一个已排序的链表的头 head &#xff0c; 删除原始链表中所有重复数字的节点&#xff0c;只留下不同的数字 。返回 已排序的链表 。 示例 1&#xff1a; 输入&#xff1a;head [1,2,3,3,4,4,5] 输出&#xff1a;[1,2,5] 解题思路 由于链表…
阅读更多...
【小呆的力学笔记】连续介质力学的知识点回顾一：运动和变形

【小呆的力学笔记】连续介质力学的知识点回顾一：运动和变形

文章目录 1. 运动的描述2. 拉格朗日描述下的变形2.1 线元的变化2.2 体元的变化2.3 面元的变化 1. 运动的描述 在连续介质力学中&#xff0c;存在着两种对运动的描述&#xff0c;一种为拉格朗日描述&#xff0c;即通过描述每个物质点的运动来描述整个变形体的运动&#xff0c;也…
阅读更多...
电脑如何远程访问？

电脑如何远程访问？

【天联】的使用场景 电脑远程访问在现代科技的发展中扮演了重要的角色。对于企业和个人用户来说&#xff0c;远程访问的便利性提供了许多机会和可能性。作为一种高效的工具&#xff0c;【天联】具有广泛的应用场景&#xff0c;可以实现异地统一管理、协同办公以及远程数据采集…
阅读更多...
一文了解MyBatis

一文了解MyBatis

文章目录 MyBatis1. MyBatis的执行流程2. MyBatis是否支持延迟加载3. MyBatis延迟加载的底层原理4. MyBatis的二级缓存机制用过吗5. 谈谈MyBatis框架的优势6. 简单描述MyBatis的工作原理7. MyBatis中的sql标签8. MyBatis中的${}和#{}的区别9. MyBatis中ResulyMap的作用[重要]10…
阅读更多...
在Python中实现限定抽奖次数的机制

在Python中实现限定抽奖次数的机制

目录 一、引言 二、需求分析 三、设计思路 四、代码实现 4.1 使用字典存储用户抽奖次数 4.2 使用数据库存储用户抽奖次数 五、扩展与优化 六、总结 一、引言 在当今互联网应用中&#xff0c;抽奖系统作为吸引用户、提高用户参与度和活跃度的重要手段&#xff0c;已经被…
阅读更多...
展望跨境智慧银行在全球化金融服务中的发展趋势和机遇

展望跨境智慧银行在全球化金融服务中的发展趋势和机遇

一、引言 随着全球经济的不断融合和金融科技的迅猛发展，跨境智慧银行作为连接不同国家和地区金融市场的桥梁，正逐渐展现出其独特的魅力和潜力。跨境支付与结算作为跨境智慧银行的核心业务之一，随着全球化的深入发展和国际贸易的日益频繁，其业务场景也愈发丰富和复杂。本文…
阅读更多...
【智能算法应用】灰狼算法GWO求解三维路径规划问题

【智能算法应用】灰狼算法GWO求解三维路径规划问题

目录 1.算法原理2.三维路径规划数学模型3.结果展示4.参考文献5.代码获取 1.算法原理 【智能算法】灰狼算法&#xff08;GWO&#xff09;原理及实现 2.三维路径规划数学模型 三维地形可以等效处理成山峰地形&#xff0c;数学模型为: z ( x , y ) h 0 ∑ j 1 N h j max ⁡…
阅读更多...
Vitis HLS 学习笔记--块级控制协议-ap_ctrl_chain/ap_ctrl_hs/ap_ctrl_none

Vitis HLS 学习笔记--块级控制协议-ap_ctrl_chain/ap_ctrl_hs/ap_ctrl_none

目录 1. 简介 2. 详细分析 2.1 使用场景区别 2.2 ap_continue 行为详解 2.3 ap_ctrl_chain 行为详解 3. 总结 1. 简介 块级控制协议允许硬件模块表明&#xff1a; 何时可以开始处理数据。何时完成了数据处理。以及何时处于空闲状态&#xff0c;准备接受新的数据输入。 …
阅读更多...
【放球问题】920. 播放列表的数量

【放球问题】920. 播放列表的数量

本文涉及知识点 【组合数学 隔板法 容斥原理】放球问题 本题同解 【动态规划】【组合数学】【C算法】920播放列表的数量 LeetCode 920. 播放列表的数量 你的音乐播放器里有 n 首不同的歌&#xff0c;在旅途中&#xff0c;你计划听 goal 首歌&#xff08;不一定不同&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023