1. 运动的描述

在连续介质力学中，存在着两种对运动的描述，一种为拉格朗日描述，即通过描述每个物质点的运动来描述整个变形体的运动，也称为物质描述，另外一种为欧拉描述，即通过描述每个空间位置点物理量来描述整个变形体的运动，也称空间描述。下面我们通过一些说明来梳理清两者的内容和区别。
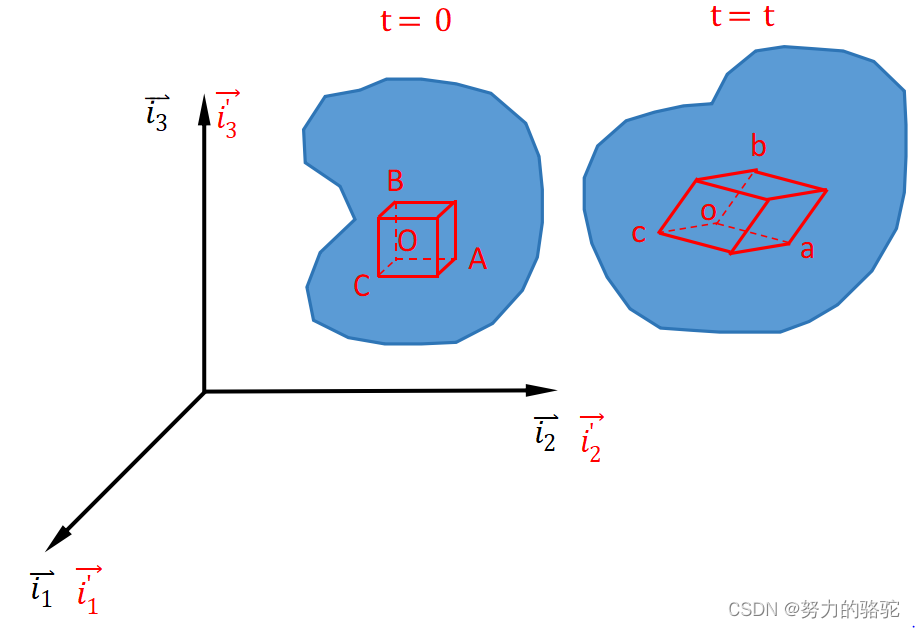
假设在$t=0$时刻，变形体在空间中的位置如下图所示，其中$\overrightarrow{i_1}、\overrightarrow{i_2}、\overrightarrow{i_3}$ 为此时空间坐标系，$\overrightarrow{i_1^{{}^{\prime }}}、\overrightarrow{i_2^{{}^{\prime }}}、\overrightarrow{i_3^{{}^{\prime }}}$ 为固结在此变形体上的直角坐标系，经过$t$时间后，变形体发生运动和变形，其位形（位置和形状）变成下图右侧所示，此时固结于变形体的坐标系将发生角度和长度的变化，其不一定能够继续保持直角坐标系，而是成为下图右侧黄色斜体坐标系的形式。

现在我们来讨论变形体的运动，在拉格朗日描述中，我们关注的是物质点的运动，例如在上图中的P点，在$t=0$时刻，P点在$\overrightarrow{i_1^{{}^{\prime }}}\overrightarrow{i_2^{{}^{\prime }}}\overrightarrow{i_3^{{}^{\prime }}}$ 中的坐标为$<x_1^{{}^{\prime }},x_2^{{}^{\prime }},x_3^{{}^{\prime }}>$，在$\overrightarrow{i_1}\overrightarrow{i_2}\overrightarrow{i_3}$ 中的坐标可由下式确定
$$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OA}+<x_1^{{}^{\prime }},x_2^{{}^{\prime }},x_3^{{}^{\prime }}>\text{\hspace{1em}(1.1)}$$
在$t$时刻，P点运动至P‘点，此时P‘点在固结于变形体的$\overrightarrow{i_1^{{}^{\prime }}}\overrightarrow{i_2^{{}^{\prime }}}\overrightarrow{i_3^{{}^{\prime }}}$的坐标已经不容易表示了，我们直接记录P‘在$\overrightarrow{i_1}\overrightarrow{i_2}\overrightarrow{i_3}$ 空间坐标系中的位置坐标为$<x_1,x_2,x_3>$，显然这与P点初始坐标和时间是相关的，当取相应的坐标系使得$\overrightarrow{OA}=0$，且$\overrightarrow{i_1^{{}^{\prime }}}\overrightarrow{i_2^{{}^{\prime }}}\overrightarrow{i_3^{{}^{\prime }}}$ 与$\overrightarrow{i_1}\overrightarrow{i_2}\overrightarrow{i_3}$ 坐标轴平行，即初始固结于变形体的坐标系和空间坐标系取一致坐标系，此时，P点初始空间坐标即为$<x_1^{{}^{\prime }},x_2^{{}^{\prime }},x_3^{{}^{\prime }}>$，那么 $x_i=x_i(x_j^{{}^{\prime }},t)$，那么此时物质点P点的位移为
$$u_i=x_i(x_j^{{}^{\prime }},t)-x_i^{{}^{\prime }}\text{\hspace{1em}(1.2)}$$

接下来，我们来看看欧拉描述下，变形体的运动。在欧拉描述中，我们将关注空间中的某一位置点，比如我们关注空间位置点P’点，该点的空间位置坐标为$<x_1,x_2,x_3>$，当$t=t$时，有一个$t=0$时刻处于P点的物质点此时占据该位置（当$t=t^{{}^{\prime }}$时，占据该位置的物质可能是$t=0$时刻的其他物质点）。因此，当$t=t$时占据空间位置点P’点的物质，在$t=0$时该物质点的初始坐标为$x_i^{{}^{\prime }}=x_i^{{}^{\prime }}(x_j,t)$。那么此时，位移由下式确定
$$u_i=x_i-x_i^{{}^{\prime }}(x_j,t)\text{\hspace{1em}(1.3)}$$

2. 拉格朗日描述下的变形

2.1 线元的变化

接下来，我们来讨论拉格朗日描述下变形体的变形。坐标系仍然是将$t=0$时刻的固结与变形体的坐标系$\overrightarrow{i_1^{{}^{\prime }}}\overrightarrow{i_2^{{}^{\prime }}}\overrightarrow{i_3^{{}^{\prime }}}$和空间坐标系$\overrightarrow{i_1}\overrightarrow{i_2}\overrightarrow{i_3}$ 选为统一坐标系，如下图所示。

此时，$t=0$时刻的微元六面体OABC在$t=t$时刻变成微元六面体oabc。其中设O点坐标为变形体在变形前的坐标（即在初始固结于变形体的$\overrightarrow{i_1^{{}^{\prime }}}\overrightarrow{i_2^{{}^{\prime }}}\overrightarrow{i_3^{{}^{\prime }}}$坐标系下）为$<x_1^{{}^{\prime }},x_2^{{}^{\prime }},x_3^{{}^{\prime }}>$，A点坐标为$<x_1^{{}^{\prime }}+d{x}_1^{{}^{\prime }},x_2^{{}^{\prime }}+d{x}_2^{{}^{\prime }},x_3^{{}^{\prime }}+d{x}_3^{{}^{\prime }}>$，经过t时间后，变形前微元OA变为微元oa，同时用变形后的坐标来表示，那么o点空间坐标为$<x_1,x_2,x_3>$，a点空间坐标为$<x_1+d{x}_1,x_2+d{x}_2,x_3+d{x}_3>$，上述坐标有以下关系
$$\begin{gathered} x_i=x_i(x_j^{{}^{\prime }},t) \\ {x}_i+d{x}_i=x_i(x_j^{{}^{\prime }}+d{x}_j^{{}^{\prime }},t)\text{\hspace{1em}(2.1)} \end{gathered}$$
那么，不难得到
$$\begin{array}{rl}d{x}_i& =x_i(x_j^{{}^{\prime }}+d{x}_j^{{}^{\prime }},t)-x_i(x_j^{{}^{\prime }},t)\\ & =x_i(x_j^{{}^{\prime }},t)+\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}-x_i(x_j^{{}^{\prime }},t)\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(2.2)}$$
以$d{x}_1$为例，有
$$d{x}_1=\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}d{x}_1^{{}^{\prime }}+\frac{\partial x_1}{\partial x_2^{{}^{\prime }}}d{x}_2^{{}^{\prime }}+\frac{\partial x_1}{\partial x_3^{{}^{\prime }}}d{x}_3^{{}^{\prime }}\text{\hspace{1em}(2.3)}$$

其中第一项即为线元沿$\overrightarrow{i_1^{{}^{\prime }}}$方向的伸长，第二项为线元从$\overrightarrow{i_1^{{}^{\prime }}}$向$\overrightarrow{i_2^{{}^{\prime }}}$转动引起$\overrightarrow{i_1^{{}^{\prime }}}$投影的伸长量，第三项线元从$\overrightarrow{i_1^{{}^{\prime }}}$向$\overrightarrow{i_3^{{}^{\prime }}}$转动引起$\overrightarrow{i_1^{{}^{\prime }}}$投影的伸长量。

同理，设B点坐标为$<x_1^{{}^{\prime }}+\delta x_1^{{}^{\prime }},x_2^{{}^{\prime }}+\delta x_2^{{}^{\prime }},x_3^{{}^{\prime }}+\delta x_3^{{}^{\prime }}>$，b点坐标为$<x_1+\delta x_1,x_2+\delta x_2,x_3+\delta x_3>$，那么有

$$\begin{array}{rl}\delta x_i& =x_i(x_j^{{}^{\prime }}+\delta x_j^{{}^{\prime }},t)-x_i(x_j^{{}^{\prime }},t)\\ & =x_i(x_j^{{}^{\prime }},t)+\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\delta x_j^{{}^{\prime }}-x_i(x_j^{{}^{\prime }},t)\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\delta x_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(2.4)}$$

设C点坐标为$<x_1^{{}^{\prime }}+\Delta x_1^{{}^{\prime }},x_2^{{}^{\prime }}+\Delta x_2^{{}^{\prime }},x_3^{{}^{\prime }}+\Delta x_3^{{}^{\prime }}>$，b点坐标为$<x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3>$，那么有

$$\begin{array}{rl}\Delta x_i& =x_i(x_j^{{}^{\prime }}+\Delta x_j^{{}^{\prime }},t)-x_i(x_j^{{}^{\prime }},t)\\ & =x_i(x_j^{{}^{\prime }},t)+\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\Delta x_j^{{}^{\prime }}-x_i(x_j^{{}^{\prime }},t)\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\Delta x_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(2.5)}$$

2.2 体元的变化

那么，变形后，六面体微元体积变化为
$$\begin{gathered} dV=[\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}]=\left|\begin{array}{ccc}d{x}_1& d{x}_2& d{x}_3\\ \delta x_1& \delta x_2& \delta x_3\\ \Delta x_1& \Delta x_2& \Delta x_3\end{array}\right| \\ =\left|\begin{array}{ccc}\frac{\partial x_1}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}& \frac{\partial x_2}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}& \frac{\partial x_3}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}\\ \frac{\partial x_1}{\partial x_j^{{}^{\prime }}}\delta x_j^{{}^{\prime }}& \frac{\partial x_2}{\partial x_j^{{}^{\prime }}}\delta x_j^{{}^{\prime }}& \frac{\partial x_3}{\partial x_j^{{}^{\prime }}}\delta x_j^{{}^{\prime }}\\ \frac{\partial x_1}{\partial x_j^{{}^{\prime }}}\Delta x_j^{{}^{\prime }}& \frac{\partial x_2}{\partial x_j^{{}^{\prime }}}\Delta x_j^{{}^{\prime }}& \frac{\partial x_3}{\partial x_j^{{}^{\prime }}}\Delta x_j^{{}^{\prime }}\end{array}\right| \\ =\left|\begin{array}{ccc}d{x}_1^{{}^{\prime }}& d{x}_2^{{}^{\prime }}& d{x}_3^{{}^{\prime }}\\ \delta x_1^{{}^{\prime }}& \delta x_2^{{}^{\prime }}& \delta x_3^{{}^{\prime }}\\ \Delta x_1^{{}^{\prime }}& \Delta x_2^{{}^{\prime }}& \Delta x_3^{{}^{\prime }}\end{array}\right|\cdot \left|\begin{array}{ccc}\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_2^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\end{array}\right|\text{\hspace{1em}(2.6)} \end{gathered}$$

（体积为$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$混合积）
我们定义变形梯度矩阵为
$$F={\left[\begin{array}{ccc}\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_2^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\end{array}\right]}^T\text{\hspace{1em}(2.7)}$$
变形梯度类似小变形假设下的应变矩阵，包含了线元伸长和转动等信息。
高等数学的知识，不难得出变形梯度行列式为Jaccobi行列式，即
$$J=\left|\begin{array}{ccc}\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_1}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_1}{\partial x_3^{{}^{\prime }}}\\ \frac{\partial x_2}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_3^{{}^{\prime }}}\\ \frac{\partial x_3}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\end{array}\right|=\left|\begin{array}{ccc}\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_1^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_2^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_2^{{}^{\prime }}}\\ \frac{\partial x_1}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_2}{\partial x_3^{{}^{\prime }}}& \frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\end{array}\right|\text{\hspace{1em}(2.8)}$$

那么上式（2.6）变为
$$dV=Jd{V}_0\text{\hspace{1em}(2.9)}$$

2.3 面元的变化

变形后，一个面元变化为下图，其中面元 $\boxed{}OAB$存在在变形前的变形体中，也就是初始构形中，面元$\boxed{}oab$存在在变形后的变形体中，也就是即时构形中。

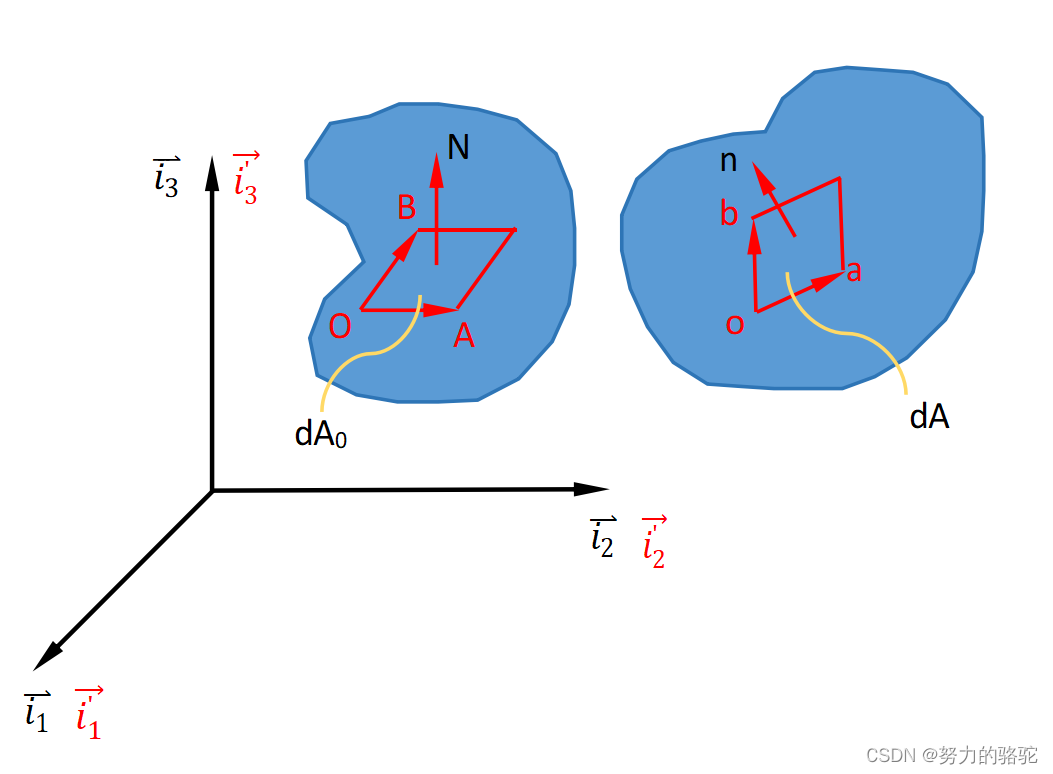
其中对有向面元有下式成立
$$\begin{array}{rl}\overrightarrow{N}d{A}_0& =\overrightarrow{OA}\otimes \overrightarrow{OB}\\ & =\left|\begin{array}{ccc}\overrightarrow{i_1}& \overrightarrow{i_2}& \overrightarrow{i_3}\\ d{x}_1^{{}^{\prime }}& d{x}_2^{{}^{\prime }}& d{x}_3^{{}^{\prime }}\\ \delta x_1^{{}^{\prime }}& \delta x_2^{{}^{\prime }}& \delta x_3^{{}^{\prime }}\end{array}\right|\\ & =\overrightarrow{i_1}(d{x}_2^{{}^{\prime }}\delta x_3^{{}^{\prime }}-d{x}_3^{{}^{\prime }}\delta x_2^{{}^{\prime }})+\overrightarrow{i_2}(d{x}_3^{{}^{\prime }}\delta x_1^{{}^{\prime }}-d{x}_1^{{}^{\prime }}\delta x_3^{{}^{\prime }})+\overrightarrow{i_3}(d{x}_1^{{}^{\prime }}\delta x_2^{{}^{\prime }}-d{x}_2^{{}^{\prime }}\delta x_1^{{}^{\prime }})\end{array}\text{\hspace{1em}(2.10)}$$

$$\begin{array}{rl}\overrightarrow{n}dA& =\overrightarrow{oa}\otimes \overrightarrow{ob}\\ & =\left|\begin{array}{ccc}\overrightarrow{i_1}& \overrightarrow{i_2}& \overrightarrow{i_3}\\ d{x}_1& d{x}_2& d{x}_3\\ \delta x_1& \delta x_2& \delta x_3\end{array}\right|\\ & =\overrightarrow{i_1}(d{x}_2\delta x_3-d{x}_3\delta x_2)+\overrightarrow{i_2}(d{x}_3\delta x_1-d{x}_1\delta x_3)+\overrightarrow{i_3}(d{x}_1\delta x_2-d{x}_2\delta x_1)\end{array}\text{\hspace{1em}(2.11)}$$
当然，上两式可以用Einstein 标记法其分量形式为
$$\begin{array}{rl}{N}_{i}d{A}_0\overrightarrow{i_i}& =e_{ijk}\overrightarrow{i_i}d{x}_j^{{}^{\prime }}\delta x_k^{{}^{\prime }}\end{array}\text{\hspace{1em}(2.10’)}$$

$$\begin{array}{rl}{n}_{i}dA\overrightarrow{i_i}& =e_{ijk}\overrightarrow{i_i}d{x}_j\delta x_k\end{array}\text{\hspace{1em}(2.11’)}$$
对于式（2.11‘），有
$$\begin{array}{rl}{n}_{i}dA& =e_{ijk}d{x}_j\delta x_k\\ & =e_{ijk}\frac{\partial x_j}{\partial x_l^{{}^{\prime }}}d{x}_l^{{}^{\prime }}\cdot \frac{\partial x_k}{\partial x_m^{{}^{\prime }}}\delta x_m^{{}^{\prime }}\\ & =e_{ijk}\frac{\partial x_j}{\partial x_l^{{}^{\prime }}}\frac{\partial x_k}{\partial x_m^{{}^{\prime }}}d{x}_l^{{}^{\prime }}\delta x_m^{{}^{\prime }}\end{array}\text{\hspace{1em}(2.12)}$$
对上式左乘$\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}$，有
$$\begin{array}{rl}\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}{n}_{i}dA& =e_{ijk}\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}\frac{\partial x_j}{\partial x_l^{{}^{\prime }}}\frac{\partial x_k}{\partial x_m^{{}^{\prime }}}d{x}_l^{{}^{\prime }}\delta x_m^{{}^{\prime }}\\ & =J\cdot e_{plm}d{x}_l^{{}^{\prime }}\delta x_m^{{}^{\prime }}\\ & =J{N}_{p}d{A}_0\end{array}\text{\hspace{1em}(2.13)}$$

这里需要用到
$$e_{ijk}\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}\frac{\partial x_j}{\partial x_l^{{}^{\prime }}}\frac{\partial x_k}{\partial x_m^{{}^{\prime }}}=J\cdot e_{plm}$$
我们先将Jaccobi行列式展开
$$\begin{gathered} J=+\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}\frac{\partial x_2}{\partial x_2^{{}^{\prime }}}\frac{\partial x_3}{\partial x_3^{{}^{\prime }}}+\frac{\partial x_2}{\partial x_1^{{}^{\prime }}}\frac{\partial x_3}{\partial x_2^{{}^{\prime }}}\frac{\partial x_1}{\partial x_3^{{}^{\prime }}}+\frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\frac{\partial x_1}{\partial x_2^{{}^{\prime }}}\frac{\partial x_2}{\partial x_3^{{}^{\prime }}} \\ -\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}\frac{\partial x_3}{\partial x_2^{{}^{\prime }}}\frac{\partial x_2}{\partial x_3^{{}^{\prime }}}-\frac{\partial x_2}{\partial x_1^{{}^{\prime }}}\frac{\partial x_1}{\partial x_2^{{}^{\prime }}}\frac{\partial x_1}{\partial x_3^{{}^{\prime }}}-\frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\frac{\partial x_2}{\partial x_2^{{}^{\prime }}}\frac{\partial x_1}{\partial x_3^{{}^{\prime }}} \\ =e_{ijk}\frac{\partial x_i}{\partial x_1^{{}^{\prime }}}\frac{\partial x_j}{\partial x_2^{{}^{\prime }}}\frac{\partial x_k}{\partial x_3^{{}^{\prime }}} \end{gathered}$$

$$\begin{gathered} J=-\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}\frac{\partial x_2}{\partial x_3^{{}^{\prime }}}\frac{\partial x_3}{\partial x_2^{{}^{\prime }}}-\frac{\partial x_2}{\partial x_1^{{}^{\prime }}}\frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\frac{\partial x_1}{\partial x_2^{{}^{\prime }}}-\frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\frac{\partial x_1}{\partial x_3^{{}^{\prime }}}\frac{\partial x_2}{\partial x_2^{{}^{\prime }}} \\ +\frac{\partial x_1}{\partial x_1^{{}^{\prime }}}\frac{\partial x_3}{\partial x_3^{{}^{\prime }}}\frac{\partial x_2}{\partial x_2^{{}^{\prime }}}+\frac{\partial x_2}{\partial x_1^{{}^{\prime }}}\frac{\partial x_1}{\partial x_3^{{}^{\prime }}}\frac{\partial x_1}{\partial x_2^{{}^{\prime }}}+\frac{\partial x_3}{\partial x_1^{{}^{\prime }}}\frac{\partial x_2}{\partial x_3^{{}^{\prime }}}\frac{\partial x_1}{\partial x_2^{{}^{\prime }}} \\ =-e_{ijk}\frac{\partial x_i}{\partial x_1^{{}^{\prime }}}\frac{\partial x_j}{\partial x_3^{{}^{\prime }}}\frac{\partial x_k}{\partial x_2^{{}^{\prime }}} \end{gathered}$$
不难得出，$$J{e}_{plm}=e_{ijk}\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}\frac{\partial x_j}{\partial x_l^{{}^{\prime }}}\frac{\partial x_k}{\partial x_m^{{}^{\prime }}}$$
对式（2.13）左乘$\frac{\partial x_p^{{}^{\prime }}}{\partial x_j}$，那么有
$$\begin{array}{rl}& \frac{\partial x_p^{{}^{\prime }}}{\partial x_j}\frac{\partial x_i}{\partial x_p^{{}^{\prime }}}{n}_{i}dA=\frac{\partial x_p^{{}^{\prime }}}{\partial x_j}J{N}_{p}d{A}_0\\ \Rightarrow & {\delta }_{ij}{n}_{i}dA=\frac{\partial x_p^{{}^{\prime }}}{\partial x_j}J{N}_{p}d{A}_0\\ \Rightarrow & n_{j}dA=\frac{\partial x_p^{{}^{\prime }}}{\partial x_j}J{N}_{p}d{A}_0\end{array}$$
上式写成矩阵形式，如下所示
$$\begin{array}{r}\mathbf{n}\cdot dA=J\cdot \mathbf{N}\cdot {\mathbf{F}}^{-1}\cdot d{A}_0\end{array}$$