目录
- 1.算法原理
- 2.三维路径规划数学模型
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】灰狼算法(GWO)原理及实现
2.三维路径规划数学模型
三维地形可以等效处理成山峰地形,数学模型为:
z
(
x
,
y
)
=
h
0
+
∑
j
=
1
N
h
j
max
⋅
exp
{
−
[
k
j
x
⋅
(
x
−
x
j
max
)
x
j
max
]
2
−
[
k
j
y
⋅
(
y
−
y
j
max
)
y
j
max
]
2
}
(1)
\begin{aligned}&z(x,y)=h_0+\sum_{j=1}^Nh_j^{\max}\cdot\exp\left\{-\left[\frac{k_j^x\cdot(x-x_j^{\max})}{x_j^{\max}}\right]^2-\left[\frac{k_j^y\cdot(y-y_j^{\max})}{y_j^{\max}}\right]^2\right\}\end{aligned}\tag{1}
z(x,y)=h0+j=1∑Nhjmax⋅exp⎩
⎨
⎧−[xjmaxkjx⋅(x−xjmax)]2−[yjmaxkjy⋅(y−yjmax)]2⎭
⎬
⎫(1)

其中,h0 为基准地形高度,N 表示山峰数量。x , y 依次是水平投影面上的点的横、纵坐标,z 则是该水平面坐标点所对应的地形高度。
设航迹的起始点为Ps,终点为Pf ,将航迹的起始点和终点的连线沿 x 轴方向进行 n +1等分,等分点为 xi ,相对应的航迹点 Pi 坐标为(xi,yi,zi) ,避障成本
ϕ
\phi
ϕ。目标适应度函数可表示为:
f
i
t
n
e
s
s
=
∑
i
=
1
n
+
1
(
x
i
−
x
i
−
1
)
2
+
(
y
i
−
y
i
−
1
)
2
+
(
z
i
−
z
i
−
1
)
2
+
ϕ
(2)
fitness=\sum_{i=1}^{n+1}\sqrt{(x_i-x_{i-1})^2+(y_i-y_{i-1})^2+(z_i-z_{i-1})^2}+\phi\tag{2}
fitness=i=1∑n+1(xi−xi−1)2+(yi−yi−1)2+(zi−zi−1)2+ϕ(2)
3.结果展示


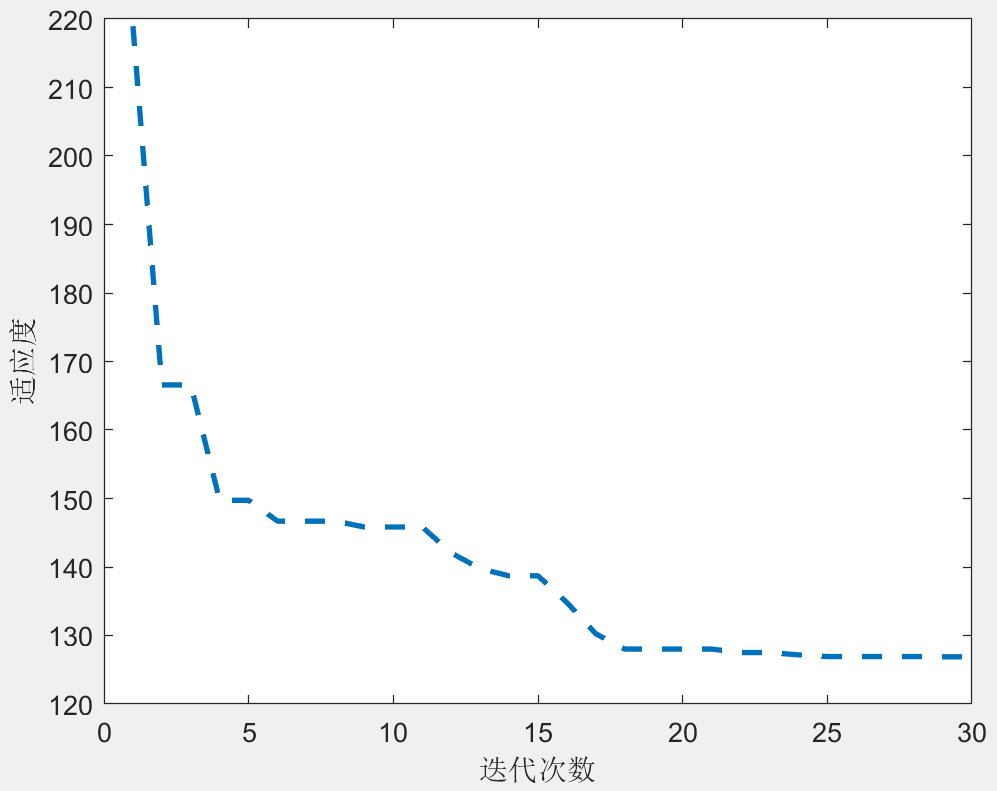
4.参考文献
[1] 刘永兰,李为民,吴虎胜,等.基于狼群算法的无人机航迹规划[J].系统仿真学报,2015,27(08):1838-1843.
[2] 解瑞云,海本斋.多策略鼠群优化算法的无人机三维航迹规划[J/OL].机械设计与制造,1-8[2024-05-28].
5.代码获取
资源清单