原文出处
KAN: Kolmogorov–Arnold Networks (arxiv.org)![]() https://arxiv.org/html/2404.19756v1
https://arxiv.org/html/2404.19756v1
论文笔记
What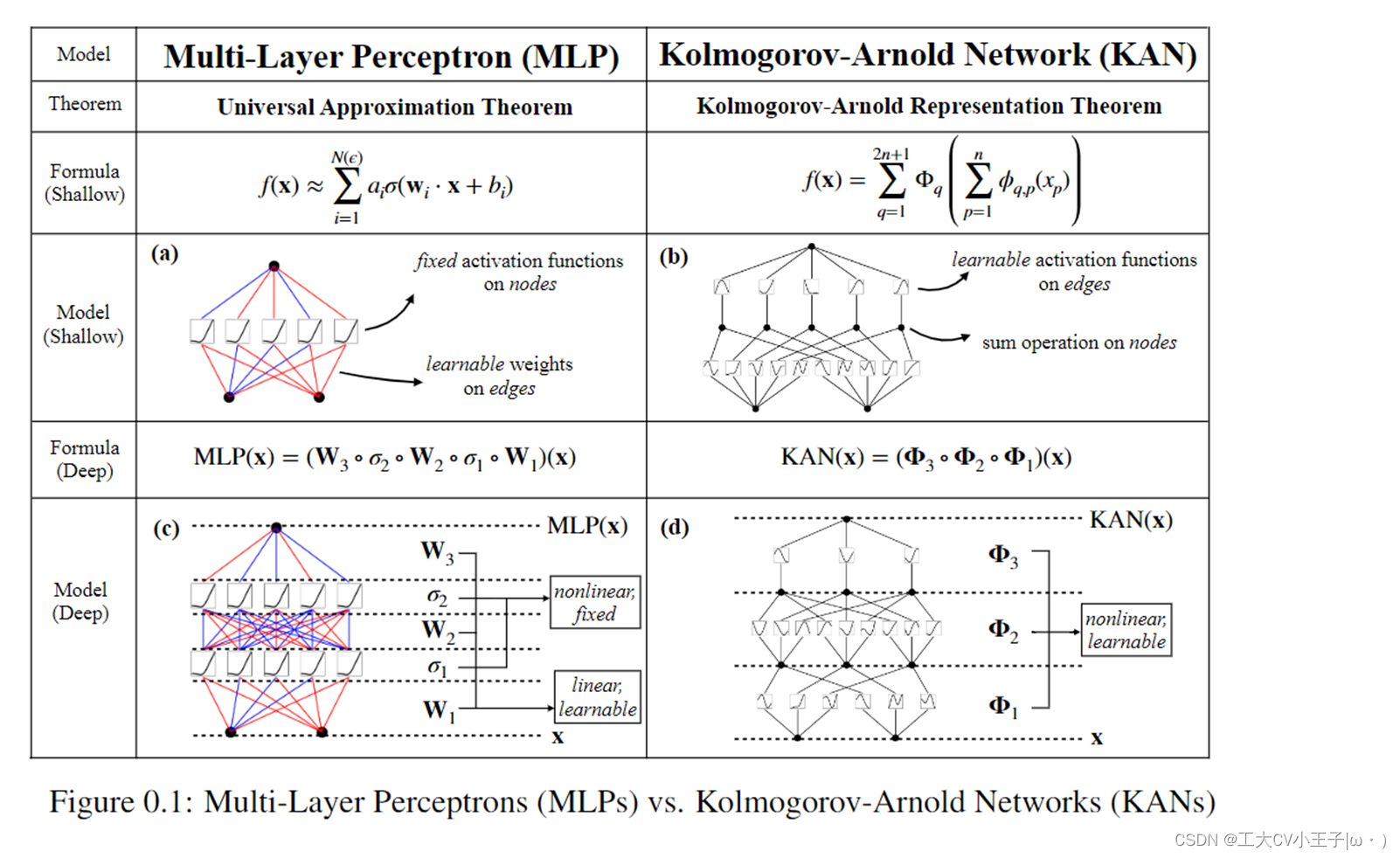
《KAN: Kolmogorov–Arnold Networks》——我们提出了 KolmogorovArnold Networks (KANs) 作为多层感知器 (MLP) 的有前途的替代方案。
我们表明,这种看似简单的变化使得 KAN 在准确性和可解释性方面优于 MLP。对于准确性,在数据拟合和 PDE 求解中,较小的 KAN 可以达到与大得多的 MLP 相当或更好的精度。从理论上和经验上讲,KAN 比 MLP 可以更快的处理神经尺度规律(faster neural scaling laws)。对于可解释性,KANs 可以直观地可视化,可以轻松与人类用户交互。通过数学和物理中的两个例子,KANs 被证明是有用的“合作者”,帮助科学家(重新)发现数学和物理规律。
Why
- 尽管 MLP 普遍使用,但它们存在重大缺陷。包括但不限于以下几条
1、梯度消失和梯度爆炸
(resnet也无法完全解除梯度消失/梯度爆炸)
2、参数效率低(激活函数是固定的,只能重复线性层+激活层的结构来增强网络的表示能力)
(这种全连接结构使得网络结构不能太稀疏,这不仅增加了计算负担,也增加了模型过拟合的风险。这就是大模型的困境,拼参数量没出路,大部分学习都是浪费掉的,效率巨低下无比,好比人海战术。)
3、处理高维数据的能力有限
mlp无法感知数据内部的空间/时序结构,因为他只是简单的全连接
4、长期依赖问题
- 一些工作[8,9,10,11,12,13]已经研究了使用Kolmogorov-Arnold表示定理来构建神经网络的可能性。然而,大多数工作都坚持原始的 depth-2 宽度 (2n + 1) 表示,并且没有机会利用更多现代技术(例如反向传播)来训练网络。就是说网络没有办法向更深的结构来发展(无法用BP来进行反向传播)
Challenge
为了准确地学习一个函数,一个模型不仅要学习组成结构(外部自由度),而且要很好地近似单变量函数(内部自由度)
- 样条对于低维函数是精确的,易于局部调整,并且能够在不同的分辨率之间切换。然而,样条曲线由于无法利用组合结构而存在严重的维数缺陷(COD)。
- 另一方面,mlp由于其特征学习而较少受到COD的影响,但由于其无法优化单变量函数,因此在低维情况下不如样条曲线准确。
- kan是样条和mlp的组合,利用各自的优势并避免各自的弱点。因为它们在外面有mlp,在里面有样条。因此,KANs不仅可以学习特征(由于它们与mlp的外部相似性),而且还可以以很高的精度优化这些学习到的特征(由于它们与样条的内部相似性)。
KAN的学习是比MLP更难的,因为它学习的是函数,但是它相较于MLP而言完成相同任务所需要的节点是更少的,相当于负责度对冲了
Idea
- mlp受到普遍近似定理的启发,而kan则受到Kolmogorov-Arnold表示定理的启发[6,7]。与mlp一样,kan具有完全连接的结构。
万能近似定理(universal approximation theorem)(Hornik et al., 1989;Cybenko, 1989) 表明,一个前馈神经网络如果具有线性输出层和至少一层具有任何一种‘‘挤压’’ 性质的激活函数(例如logistic sigmoid激活函数)的隐藏层,只要给予网络足够数量的隐藏单元,它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的Borel 可测函数。
Kolmogorov-Arnold Representation Theorem:
可以用一组较简单的非线性一元函数来表示任何一个多变量的连续函数。
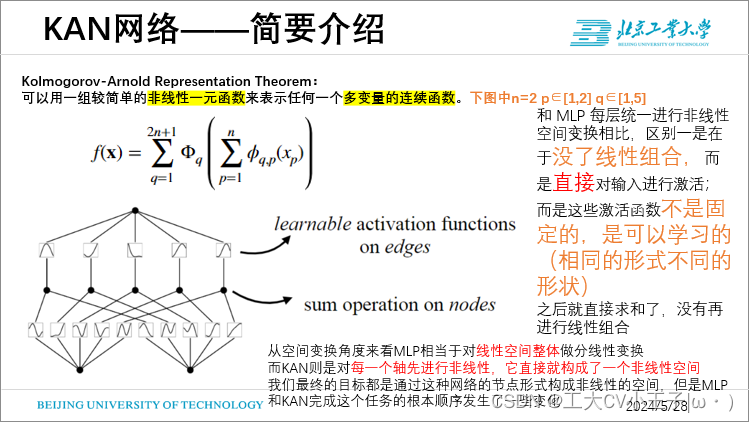
- 我们的贡献在于将原始的 Kolmogorov-Arnold 表示推广到任意宽度和深度,具体来说,放宽了公式中2n+1这种限制,KAN假设层宽相等,L层,每层N个节点。
- 至于网络的结构设计问题 原文是这样说的MLP有在节点上有固定的激活函数,而KAN在边上有可学习的激活函数
- 深层网络的设计还考虑了层级问题。图中展示的结构中,使用了两种尺度或分辨率的组合:粗粒度和细粒度网格,在保持计算效率的同时,更加精确地捕捉和适应函数的变化。这种基础结构其实并不是很难想到,以前就有了,但难点是怎么把它变深,否则单靠这么点玩意儿是不能逼近复杂函数的。这就是本文的主要贡献了。
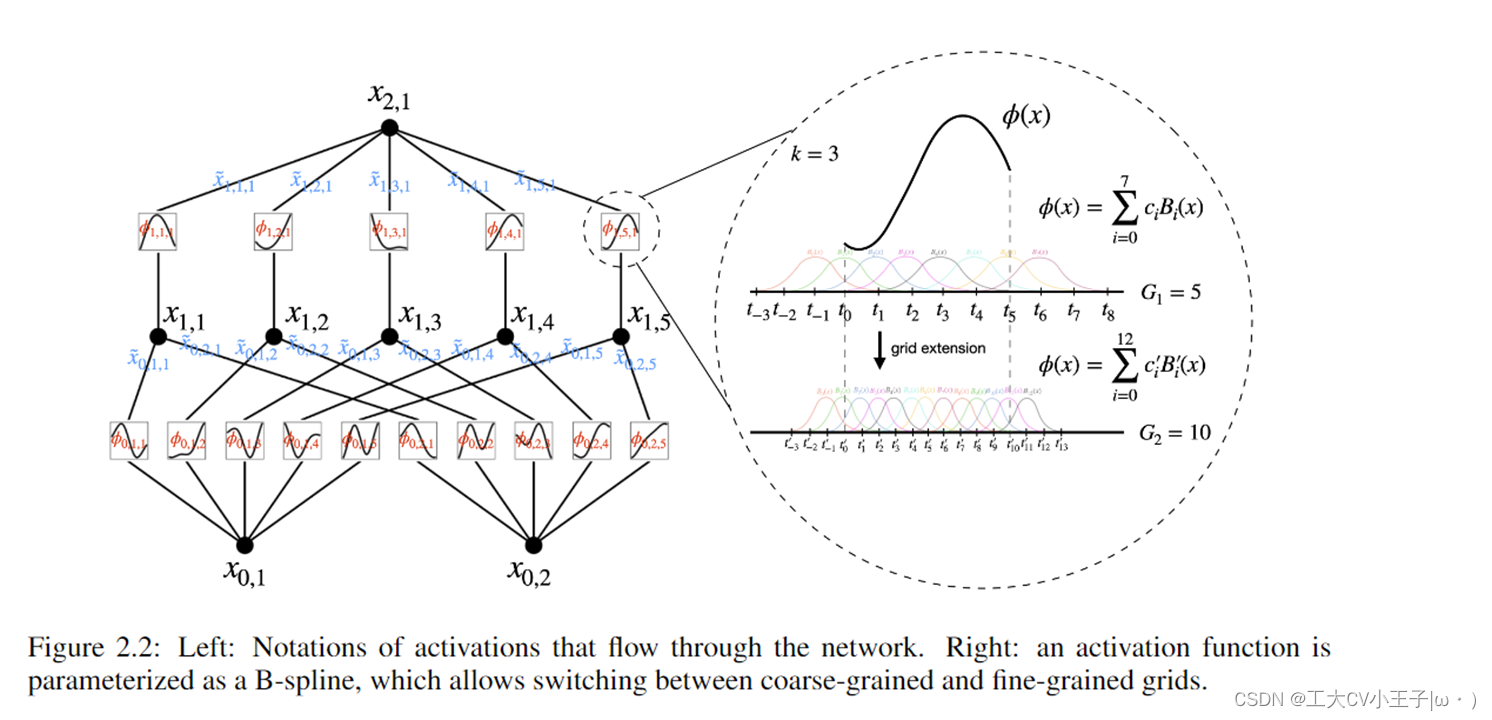
- KAN层具体实现(对照上边那个图来看)

- KAN网络执行细节(1)

- KAN网络执行细节(2)

MLP vs KAN 训练策略
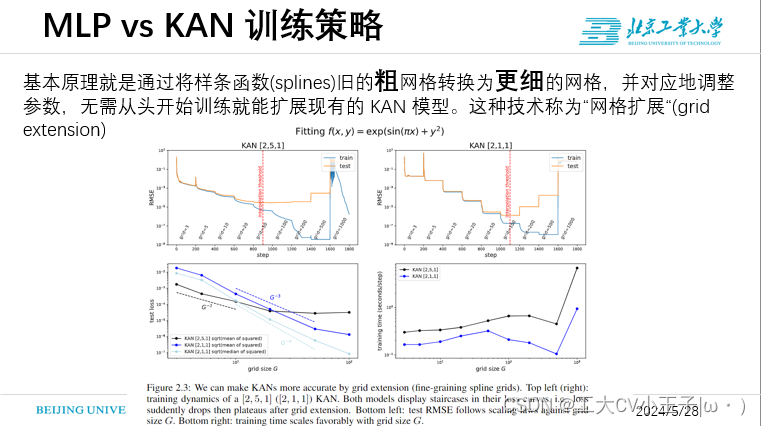

- MLP vs KAN(cost层面)

- MLP vs KAN(网络拓展与泛化)

- MLP vs KAN(模型效果)

- MLP vs KAN(可解释性)
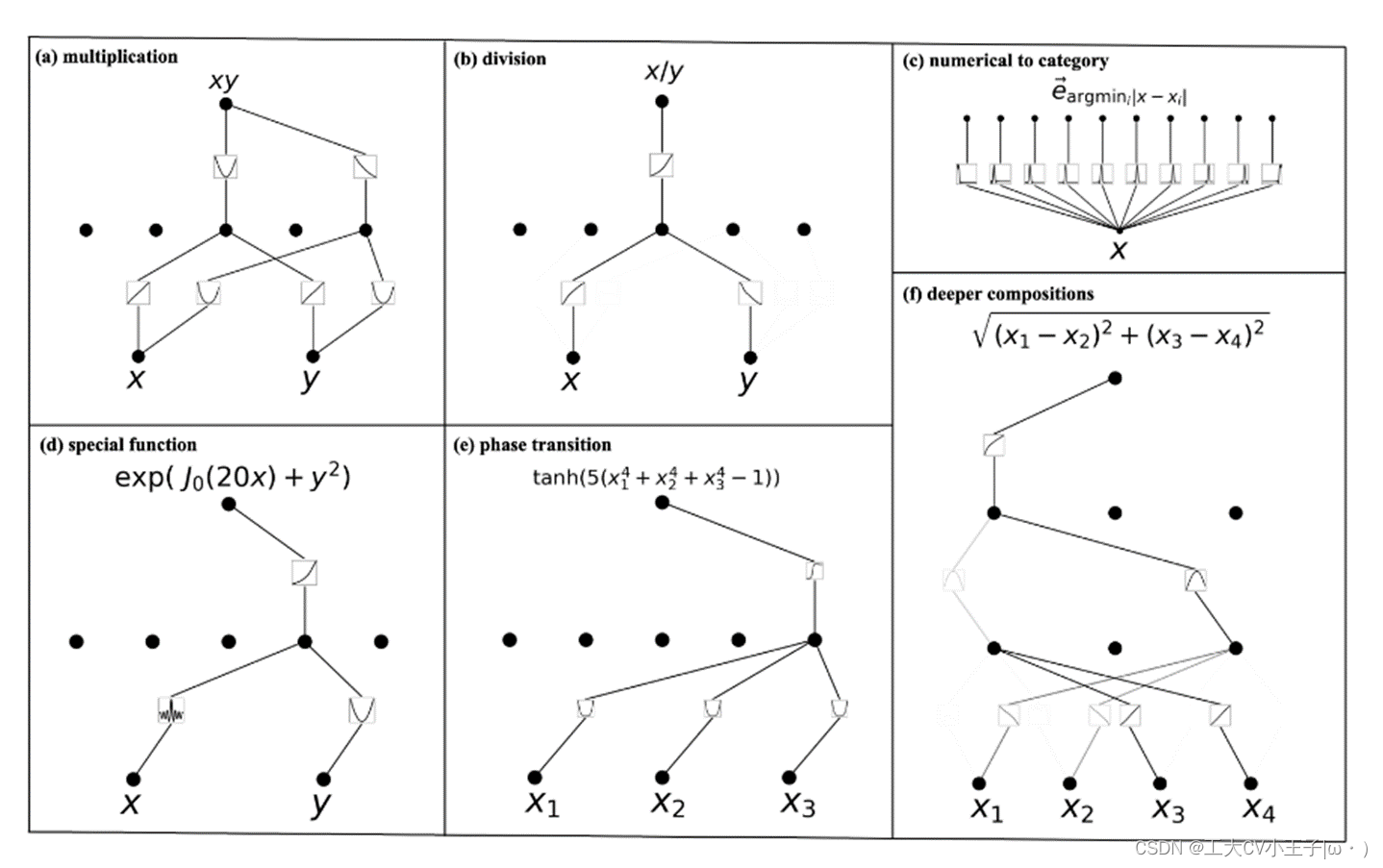
以(a)为例,xy = (x+y)^2-(x^2+y^2)自己可以对比着看一下
- kan是样条和mlp的组合,利用各自的优势并避免各自的弱点。因为它们在外面有mlp,在里面有样条。因此,KANs不仅可以学习特征(由于它们与mlp的外部相似性),而且还可以以很高的精度优化这些学习到的特征(由于它们与样条的内部相似性)。
原文翻译
Abstract(这个摘要写的真好)
受 Kolmogorov-Arnold 表示定理的启发,我们提出了 KolmogorovArnold Networks (KANs) 作为多层感知器 (MLP) 的有前途的替代方案。虽然 MLP 在节点(“神经元”)上具有固定激活函数,但 KAN 在边上(“权重”)具有可学习的激活函数。KAN 根本没有线性权重——每个权重参数都被参数化为样条的单变量函数所取代。我们表明,这种看似简单的变化使得 KAN 在准确性和可解释性方面优于 MLP。对于准确性,在数据拟合和 PDE 求解中,较小的 KAN 可以达到与大得多的 MLP 相当或更好的精度。从理论上和经验上讲,KAN 比 MLP 可以更快的处理神经尺度规律(faster neural scaling laws)。对于可解释性,KANs 可以直观地可视化,可以轻松与人类用户交互。通过数学和物理中的两个例子,KANs 被证明是有用的“合作者”,帮助科学家(重新)发现数学和物理规律。总之,KAN 是 MLP 的有前途的替代方案,为进一步改进当今严重依赖 MLP 的深度学习模型提供了机会。

1 Introduction
多层感知器 (MLP) [1, 2, 3],也称为全连接前馈神经网络,是当今深度学习模型的基础构建块。MLP 的重要性永远不会被夸大,因为它们是机器学习中近似非线性函数的默认模型,因为它们的表达能力由通用逼近定理 [3] 保证。然而,MLP 是我们可以构建的最佳非线性回归器吗?。尽管 MLP 普遍使用,但它们存在重大缺陷。例如,在Transformers [4] 中,MLP 消耗几乎所有的非嵌入参数,并且在没有后期分析工具 [5] 的情况下通常不太可解释(相对于注意力层)。
我们提出了一种有希望的mlp替代方案,称为Kolmogorov-Arnold网络(KANs)。mlp受到普遍近似定理的启发,而kan则受到Kolmogorov-Arnold表示定理的启发[6,7]。与mlp一样,kan具有完全连接的结构。然而,mlp将固定的激活函数放在节点(“神经元”)上,而kan将可学习的激活函数放在边缘(“权重”)上,如图0.1所示。因此,kan根本没有线性权矩阵:取而代之的是,每个权参数都被一个可学习的一维函数参数化为样条(learnable 1D function parametrized as a spline)所取代。KANs节点只是简单地对输入信号求和,而不应用任何非线性。有人可能会担心,由于每个MLP的权重参数都变成了KAN的样条函数,因此KAN的成本非常昂贵。幸运的是,kan通常允许比mlp更小的计算图。例如,我们表明,对于PDE求解,2层宽度-10的KAN比4层宽度-100的MLP(10−7 vs 10−5 MSE)精确100倍,参数效率高100倍(10^2 vs 10^4参数)。
不出所料,一些工作[8,9,10,11,12,13]已经研究了使用Kolmogorov-Arnold表示定理来构建神经网络的可能性。然而,大多数工作都坚持原始的 depth-2 宽度 (2n + 1) 表示,并且没有机会利用更多现代技术(例如反向传播)来训练网络。我们的贡献在于将原始的 Kolmogorov-Arnold 表示推广到任意宽度和深度,在当今深度学习世界中振兴和上下文化,以及使用大量经验实验来突出其作为 AI + Science 基础模型的潜在作用,因为它的准确性和可解释性。
尽管它们有优雅的数学解释,但kan只不过是样条和mlp的组合,利用各自的优势并避免各自的弱点。样条对于低维函数是精确的,易于局部调整,并且能够在不同的分辨率之间切换。然而,样条曲线由于无法利用组合结构而存在严重的维数缺陷(COD)。另一方面,mlp由于其特征学习而较少受到COD的影响,但由于其无法优化单变量函数,因此在低维情况下不如样条曲线准确。为了准确地学习一个函数,一个模型不仅要学习组成结构(外部自由度),而且要很好地近似单变量函数(内部自由度)。kan是这样的模型,因为它们在外面有mlp,在里面有样条。因此,KANs不仅可以学习特征(由于它们与mlp的外部相似性),而且还可以以很高的精度优化这些学习到的特征(由于它们与样条的内部相似性)。例如,给定一个高维函数

由于COD,样条对于较大的N会失败;mlp可以潜在地学习广义相加结构,但对于用ReLU激活逼近指数函数和正弦函数是非常低效的。相比之下,KANs 可以很好地学习组合结构和单变量函数,因此大大优于 MLP(见图 3.1)。

在本文中,我们将使用大量的数值实验来证明 KAN 可以显着提高 MLP 的准确性和可解释性。本文的组织如图2.1所示。在第2节中,我们介绍了KAN体系结构及其数学基础,介绍了网络简化技术,使KAN具有可解释性,并引入了网格扩展技术,使KAN更加准确。在第 3 节中,我们展示了 KAN 在数据拟合和 PDE 求解方面比 MLP 更准确:当数据中存在组合结构时,KAN 可以击败维度诅咒,比 MLP 实现了更好的缩放定律。在第 4 节中,我们展示了 KAN 是可解释的,可用于科学发现。我们使用来自数学(knot 理论)和物理(Anderson 定位)的两个示例来证明 KAN 可以帮助科学家“合作者”(重新)发现数学和物理规律。第 5 节总结了相关工作。在第 6 节中,我们通过讨论广泛的影响和未来的方向来结束。代码可在 https://github.com/KindXiaoming/pykan 获得,也可以通过 pip install pykan 安装。
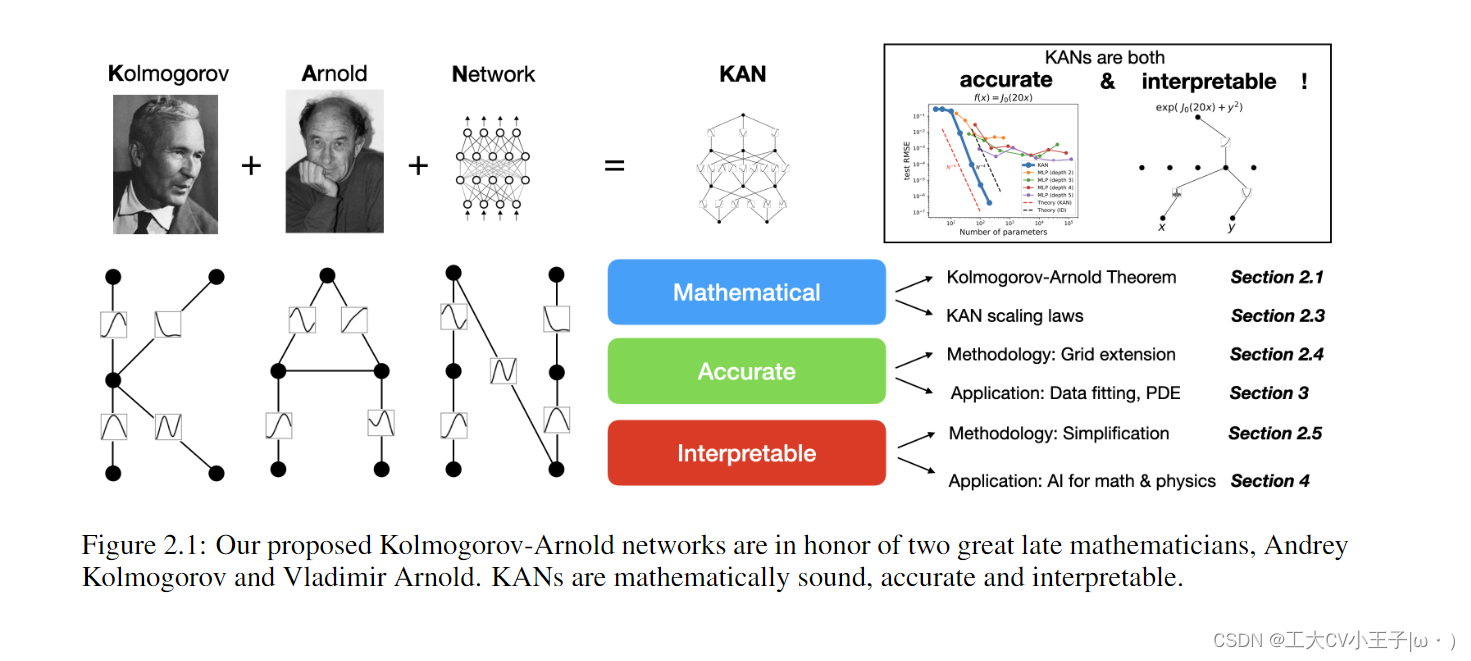
2 Kolmogorov–Arnold Networks (KAN)
多层感知器 (MLP) 受到通用逼近定理的启发。相反,我们专注于 Kolmogorov-Arnold 表示定理,该定理可以通过一种称为 Kolmogorov-Arnold 网络 (KAN) 的一种新型神经网络来实现。我们在第 2.1 节中回顾了 Kolmogorov-Arnold 定理,以激发第 2.2 节中 Kolmogorov-Arnold 网络设计。在第 2.3 节中,我们为 KAN 的表达能力及其神经缩放定律提供了理论保证。在第 2.4 节中,我们提出了一种网格扩展技术,使 KAN 越来越准确。在第 2.5 节中,我们提出了简化技术来使 KAN 可解释。
2.1 Kolmogorov-Arnold Representation theorem
Vladimir Arnold 和 Andrey Kolmogorov 确定,如果 f 是有界域上的多元连续函数,那么f可以写成单变量连续函数和二元加法运算的有限复合。(then f can be written as a finite composition of continuous functions of a single variable and the binary operation of addition.)更具体地说,对于平滑 f : [0, 1]n → R,

其中 φq,p : [0, 1] → R 和 Φq : R → R。从某种意义上说,他们表明唯一的真正的多元函数是相加的,因为所有其他函数都可以使用单变量函数和求和来编写。人们可能会天真地考虑这种用于机器学习的大新闻:学习高维函数归结为学习多项式数量的一维函数。然而,这些一维函数可以是非光滑甚至分形的,因此它们在实践中可能不是可学习的[14]。由于这种病理行为,Kolmogorov-Arnold 表示定理基本上被判决到机器学习中的死亡,被认为是理论上合理的,但实际上无用[14]。
然而,我们对 Kolmogorov-Arnold 定理对机器学习的有用性更为乐观。首先,我们不需要坚持原始方程。 (2.1),它在隐藏层中只有两层非线性和少量项 (2n + 1):我们将网络推广到任意宽度和深度。其次,科学和日常生活中的大多数功能通常是平滑的,并且具有稀疏的组成结构,可能有助于平滑的 Kolmogorov-Arnold 表示。这里的哲学接近于物理学家的心态,他们经常关心典型的情况,而不是最坏情况。毕竟,我们的物理世界和机器学习任务必须具有使物理和机器学习在所有[15]中都有用或泛化的结构。
2.2 KAN architecture
假设我们有一个由输入输出对 {xi, yi} 组成的监督学习任务,我们希望找到 f 使得所有数据点的 yi ≈ f (xi)。等式(2.1) 意味着如果我们能找到合适的单变量函数 φq,p 和 Φq 我们就成功了。这启发我们设计了一个明确参数化方程(2.1)的神经网络。由于要学习的所有函数都是单变量函数,我们可以将每个一维函数参数化为b样条曲线,具有局部b样条基函数的可学习系数(见图2.2右)。现在我们有一个 KAN 的原型,其计算图由方程式 (2.1)精确指定。如图 0.1 (b)(输入维度 n = 2)所示,显示为两层神经网络,激活函数放置在边缘而不是节点上(对节点执行简单的求和),中间层宽度为 2n + 1。


后边全是数学公式,有兴趣各位再细细研究吧
本文参考自AI大讲堂:深度学习要变天?专业拆解【KAN网络】_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1Hb421b72f/?spm_id_from=333.337.search-card.all.click&vd_source=ae3f1ec4d3d413e8531d6bbc07cd4394
https://www.bilibili.com/video/BV1Hb421b72f/?spm_id_from=333.337.search-card.all.click&vd_source=ae3f1ec4d3d413e8531d6bbc07cd4394