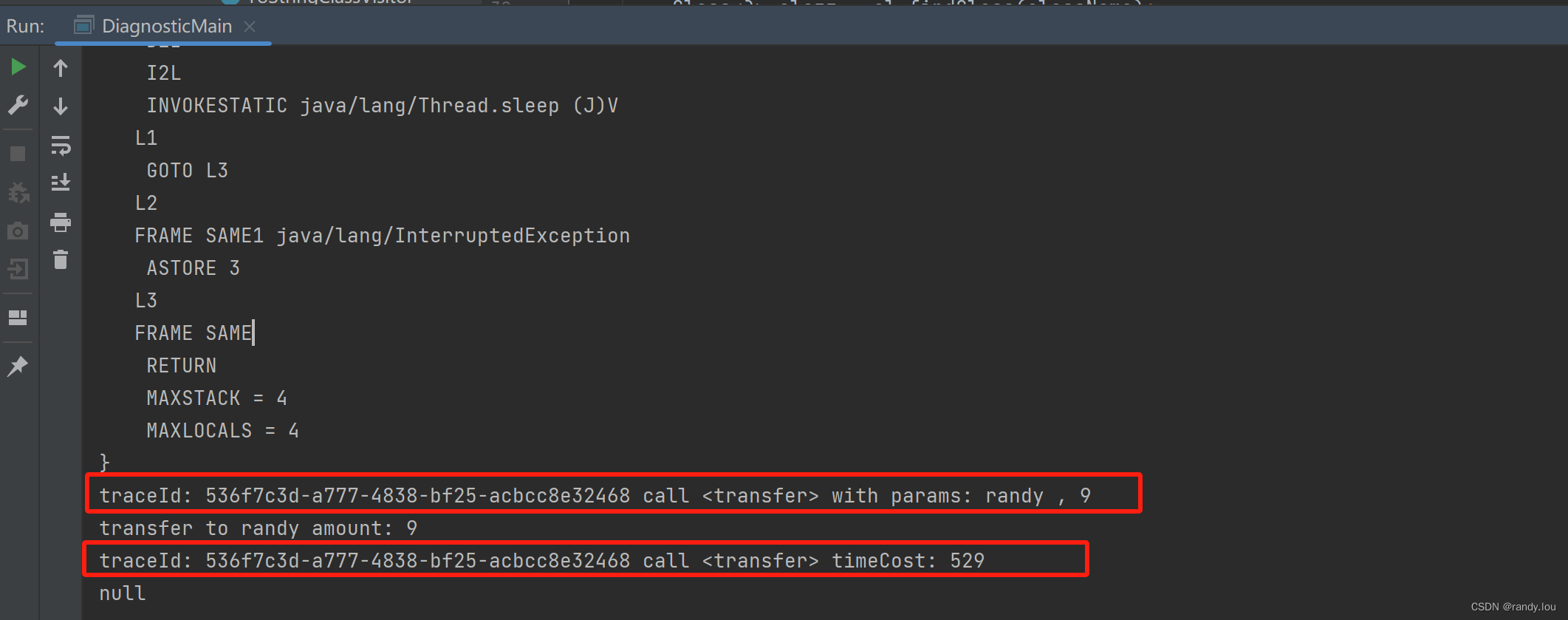
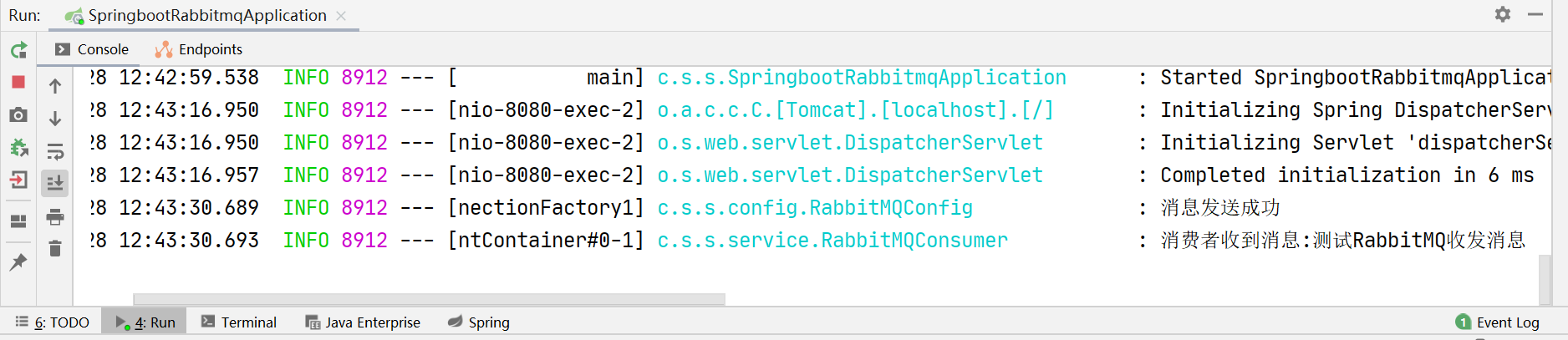
前仿真,即功能仿真。
可使用专用于仿真的工具对设计进行功能仿真,以验证电路功能是否符合设计要求。
通过功能仿真能够及时发现设计中的错误,从而加快设计进度,提高设计的可靠性。
综合后的仿真
把综合生成的标准延时反标注到综合仿真模型去,可估计门延时带来的影响,但是只能估计门延时,不能估计布线延时,仿真结果和实际情况还有一定的差距,并不十分准确。
综合后的仿真一般只在IC设计中用到,但由于目前综合工具比较成熟,大多数的软件能胜任综合工作,因此一般省去了此环节的仿真(在本书的基于Quartus II的开发中,没有进行综合后的仿真)。
布局布线后的仿真
布局布线后的仿真,即时序仿真。布局布线后生成的仿真延时文件最全,不仅包括门延时,还包括布线延时,因此最为准确,能较好地反映芯片的实际工作情况。
一般来讲,布局布线后的仿真必须进行,以确保设计的可靠性和稳定性,并可发现时序违规(Timing Violation)等时序错误,从而进一步对逻辑电路进行优化设计。
仿真包括功能仿真和时序仿真。