目录
前言
算法思想
非递归实现前序遍历
过程分析
代码
非递归实现中序遍历
过程分析
代码
非递归实现后序遍历
过程分析
代码
前言
1)前序:根 左子树 右子树
2)中序:左子树 根 右子树
3)后序:左子树 右子树 根
可以看出,这三种遍历方式的本质区别在于什么时候访问根节点,下面将介绍一种很厉害的思想,对于前中后序的非递归实现,它可以是通解。
算法思想
将二叉树分割成两部分:
1)左路节点
2)左路节点的右子树
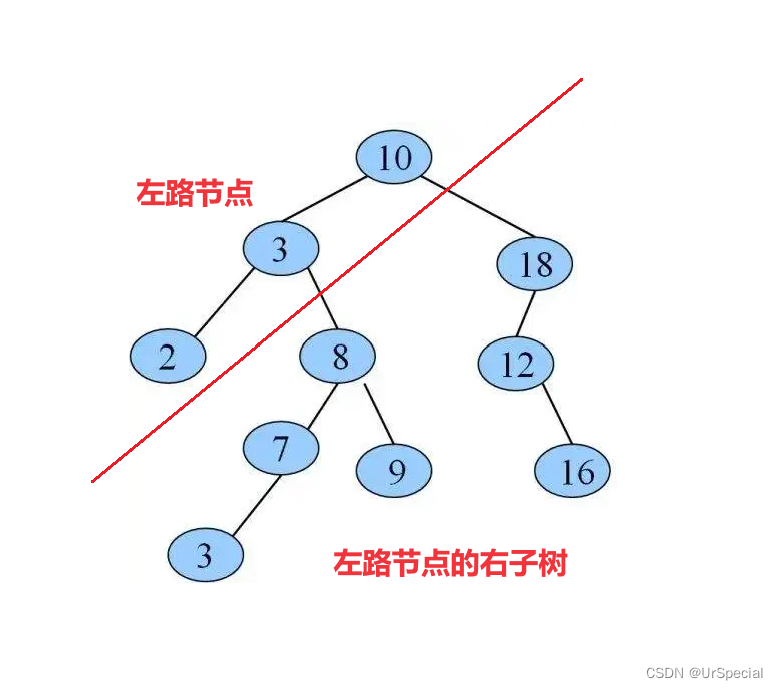
它的每一棵子树也可以继续分为左路节点和左路节点的右子树。
实现这种算法,我们需要借助一种数据结构——栈,同时,为了存储数据我们还需要借助另一种数据结构——vector。
下面,把这种算法转换成代码。
非递归实现前序遍历
过程分析
以这棵树为例:
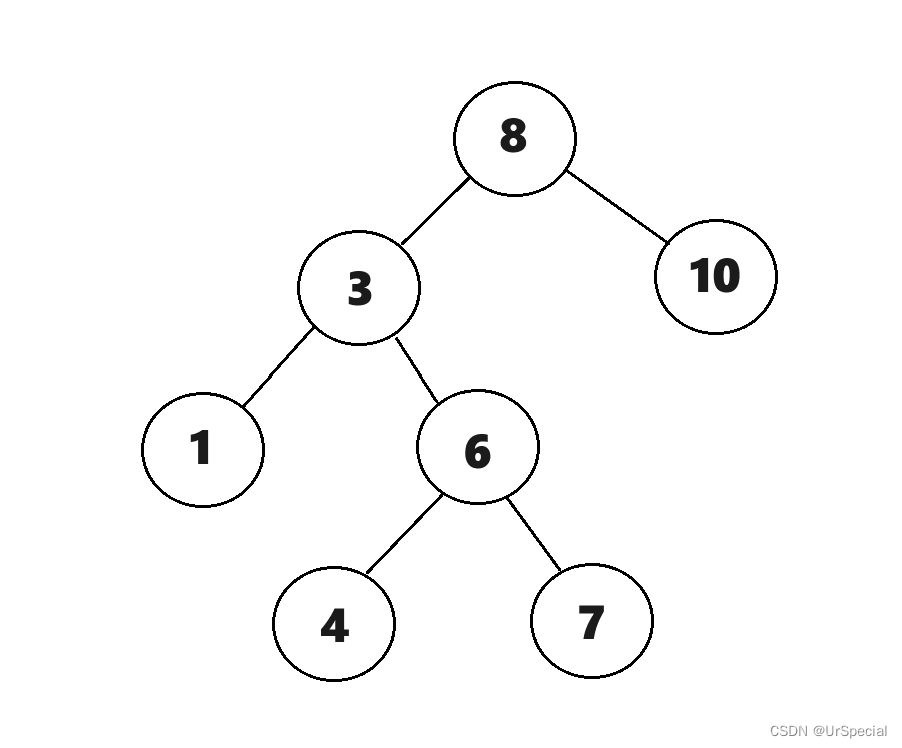
1)所有左路节点进栈。
2)根据前序遍历的规则,所遍历到的结点都可以直接反问,即可以直接保存进vector中, 因为每个节点都可以是根。
3)左路结点遍历完后,出栈,在出栈时,如果它的右子树不为空,则将它的右子树的左路节点入栈,重复此操作,就可以遍历完左路节点对应 的右子树。
以上图为例:
所有左路节点进栈(面向屏幕右手边为栈顶):
stack:8 3 1
vector:8 3 1
考虑1出栈,考虑到1的右子树为空,所以可以直接出栈。下面更新stack和vector。
stack:8 3
vector:8 3 1
考虑3出栈,考虑到3的右子树不为空,所以3出栈后,要把3的右子树的左路节点6和4依次入栈(结点3会有记录,不会找不到它的右树)。下面更新stack和vector。
stack:8 6 4
vector:8 3 1 6 4
考虑4出栈,考虑到4的右树为空,可以直接出栈。下面更新stack和vector。
stack:8 6
vector:8 3 1 6 4
考虑6出栈,考虑到6的右子树不为空,所以出栈后,它的右子树的左路节点7要入栈。下面更新stack和vector。
stack:8 7
vector:8 3 1 6 4 7
考虑7出栈,考虑到7的右子树为空,所以可以直接出栈。下面更新stack和vector。
stack:8
vector:8 3 1 6 4 7
考虑8出栈,考虑到8的右子树不为空,所以出栈后,它的右子树的左路节点10要入栈。下面更新stack和vector。
stack:10
vector:8 3 1 6 4 7 10
考虑10出栈,考虑到10的右子树为空,所以可以直接出栈。下面更新stack和vector。
stack:空
vector:8 3 1 6 4 7 10
此时,栈已空,所有结点均已访问完毕,前序遍历结束。
代码
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> ret;
TreeNode* cur = root;
while(cur || !st.empty())
{
//所有左路节点入栈
while(cur)
{
ret.push_back(cur->val);//遍历到的结点可直接访问
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
//访问当前节点的右子树,如果不为空,会进入内层的while循环,把它的左路节点入栈
//如果为空,则不会进入内存while循环
cur = top->right;
st.pop();
}
return ret;
}
};非递归实现中序遍历
过程分析
中序遍历和前序遍历尤为相似,它们的本质区别在于什么时候访问根结点。
1)所有左路节点进栈
2)左路节点进栈的同时不能去访问这些节点,因为根据中序遍历的规则,应该先访问左子树(这就是与前序遍历的区别)
3)所有左路节点都进栈以后,意味着最后一个左路节点的左子树(为空)已经访问完毕,可以访问根了,这时,弹出栈顶元素,并把它的值存 储进vector中,如果它有右子树,还应该把它的右子树的左路节点入栈。
代码
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
while(cur || !st.empty())
{
//左路节点入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
//退出循环后,意味着左路节点已访问,可以访问根了
TreeNode* top = st.top();
v.push_back(top->val);//访问根
st.pop();
cur = top->right;//左路节点的右子树如果非空,则让它的左路节点入栈
}
return v;
}
};非递归实现后序遍历
过程分析
后序遍历和前面的两种遍历方式其实差不多,都是把整棵树分为左路节点和左路节点的右子树。关键问题在于什么时候访问根。
1)左路节点进栈
2)左路节点进栈是不能直接去访问,根据后序遍历的规则,应该是先访问左子树,右子树再到根。
3)左路节点进栈完毕,意味着可以访问右子树了,如果左路节点的右子树不为空,就让它的左路节点进栈,如果为空,就可以访问根结点了
4)访问完左节点后,如果当前栈顶结点的右子树为空或者上一个访问的结点是它的右节点,满足这两个条件之一就可以访问当前节点了(根)
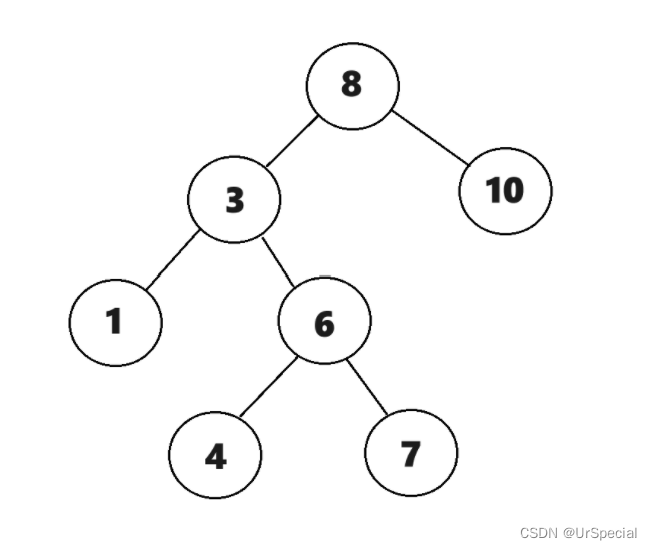
以上图为例
所有左路节点进栈(面向屏幕右手边为栈顶):
stack:8 3 1
vector:空
考虑1出栈,考虑到1的右子树为空,所以可以访问根即节点1,且1出栈。下面更新stack和vector。
stack:8 3
vector:1
考虑3出栈,考虑到3的右子树不为空,且上一个访问的节点不是它的右节点,所以3还不能访问,也还不可以出栈,要把3的右子树的左路节点6和4依次入栈 。下面更新stack和vector。
stack:8 3 6 4
vector:1
考虑4出栈,考虑到4的右树为空,可以直接出栈并访问该节点。下面更新stack和vector。
stack:8 3 6
vector:1 4
考虑6出栈,考虑到6的右子树不为空且上一个访问的结点不是它的右节点,所以不能出栈,将它的右子树的左路节点7要入栈。下面更新stack和vector。
stack:8 3 6 7
vector:1 4
这里对节点6进行了第一次判断。
考虑7出栈,考虑到7的右子树为空,所以可以直接出栈并访问。下面更新stack和vector。
stack:8 3 6
vector:1 4 7
考虑6出栈,考虑到6的右结点(7)为上一个访问的结点,所以可以访问6并将6弹出栈。下面更新stack和vector。
stack:8 3
vector:1 4 7 6
这里对节点6进行了第二次判断。可以看出,记录上一个访问的结点是有意义的。
考虑3出栈,考虑到3的右节点(6)为上一个访问的结点,所以可以访问3并弹出栈。下面更新stack和vector。
stack:8
vector:1 4 7 6 3
考虑8出栈,8的右子树不为空且它的右节点(10)不是上一个访问的结点,所以8还不可以出栈,应该将10入栈。下面更新stack和vector。
stack:8 10
vector:1 4 7 6 3
考虑10出栈,10的右树为空,可以访问,并弹出栈。下面更新stack和vector。
stack:8
vector:1 4 7 6 3 10
考虑8出栈,考虑到上一个访问的结点10为8的右节点,所以8可以访问并弹出栈。下面更新stack和vector。
stack:空
vector:1 4 7 6 3 10 8
此时,栈已空,所有结点均已访问完毕,后序遍历结束。
代码
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root, *prev = nullptr;
while(cur || !st.empty())
{
//左路节点入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
if(top->right == nullptr || prev == top->right)
{
//访问当前结点
v.push_back(top->val);
//更新prev
prev = top;
st.pop();
}
else
{
//右树的左路节点入栈
cur = top->right;
}
}
return v;
}
};完~