1,消除稳态误差
积分项目是对于历史误差进行的累积,可以理解,系统的误差累积表示不断的在减少误差,最终消除误差,这个过程需要将误差进行累加,才可以真正知道误差的大小是多少,用最终累加的误差作为积分项目,去消除误差,保证系统的稳态。
举个例子,如果系统在稳态下有一个扰动的话,这个扰动是保持的一直存在的,系统需要补偿这个扰动就需要对这个扰动误差进行累积,累积到历史的误差上面,这就是误差累积,最终到一个能够消除整个误差的状态,保证系统稳定。
其中我们会加入比例项目,是为了快速达到稳态,否则只有比例项的话,比例系数KI太小,进入系统稳态时间太长,太大会导致振荡严重,所以需要一个KP,让系统快速进入稳态,有了KP的帮助,KI就可以给的很小,便可快速进入稳态,而且KI比较小,不至于由于积分项目的变化太大,导致系统振荡。
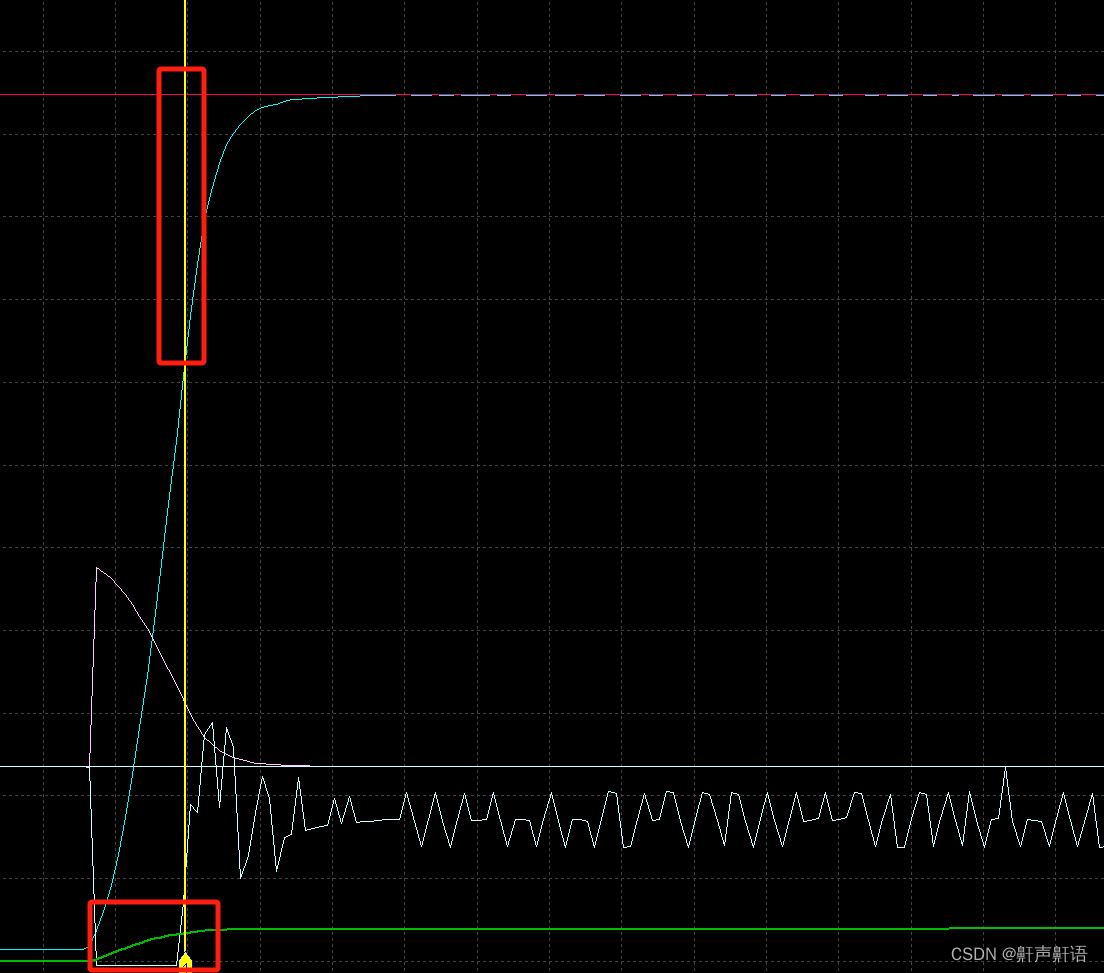
下图是只有KI的情况,振荡很厉害,如果KI参数太小,又很长的时间不会到达目标值
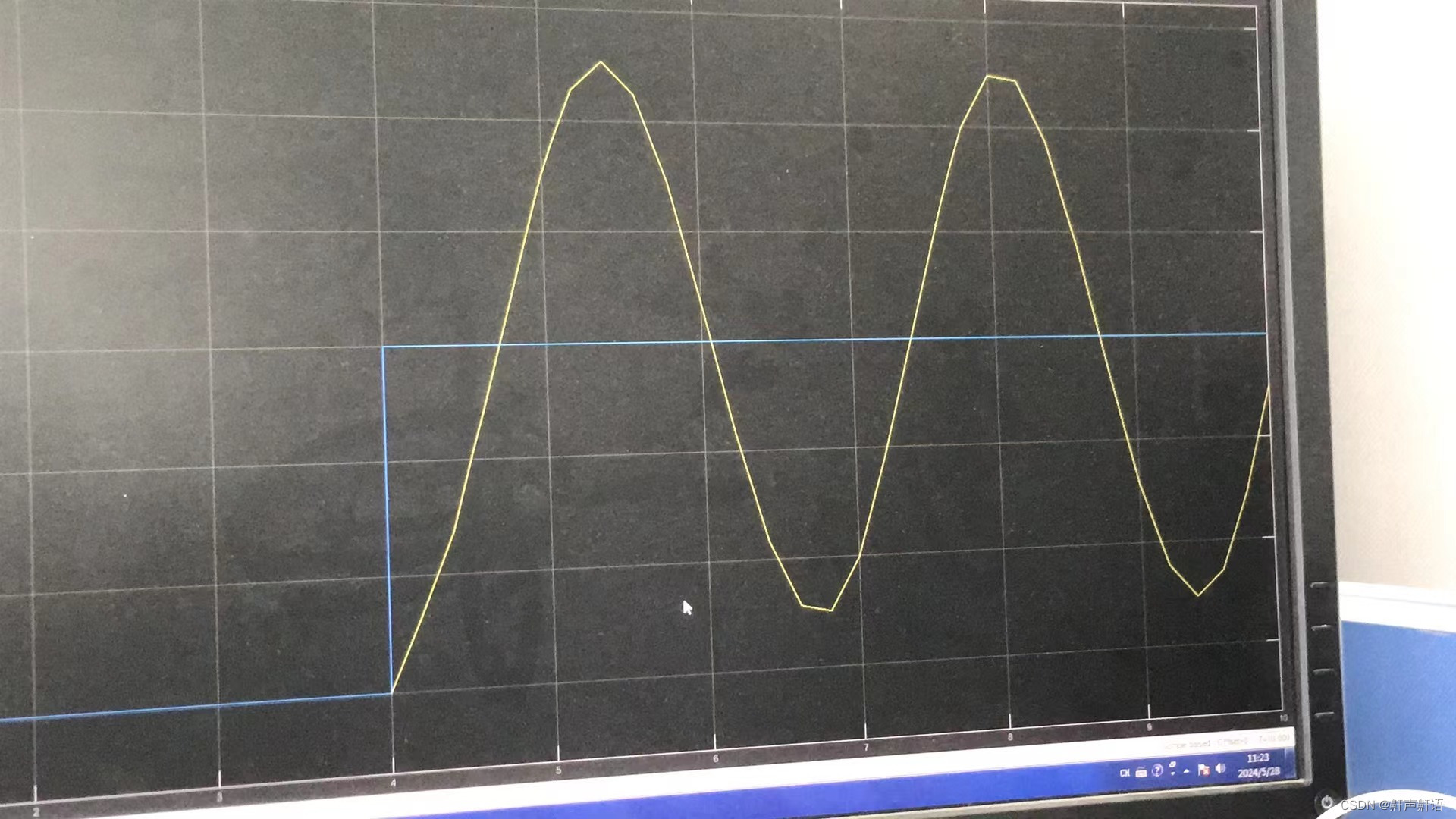
2,稳态下,积分项替代了比例项的功能?
在稳态下,积分项部分替代了比例项的功能,但不能完全替代。
- 稳态下的误差 在稳态下,系统已经达到了设定值,理想情况下误差应该为零。
- 比例项的作用 比例项的作用是使输出值与设定值成比例地变化。当误差为零时,比例项的输出也为零。
- 积分项的作用 积分项的作用是对过去所有误差进行累积,并将其转化为控制器的输出。在稳态情况下,误差为零,积分项会停止累积,但其累积值不会消失。
- 积分项替代比例项的部分功能 由于积分项的累积值不会消失,因此在稳态下,积分项会提供一部分输出,以维持系统的稳定。 这部分输出部分替代了比例项的功能。
- 积分项不能完全替代比例项 如果完全取消比例项,则系统在受到扰动时可能无法做出响应,导致输出值偏离设定值。 因此,即使在稳态下,也需要保留一定的比例项,以保证系统的快速响应能力。
- 总结 在稳态下,积分项部分替代了比例项的功能,但不能完全替代。 积分项可以维持系统的稳定,但比例项可以提高系统的响应速度。 在实际应用中,我们需要根据具体的控制要求来选择合适的比例增益和积分增益。 以下是一些相关示例: 水箱液位控制系统:
在稳态下,积分项可以使液位保持在设定值,而无需比例项的输出。 电机转速控制系统:
在稳态下,积分项可以使电机转速保持在设定值,但如果需要快速改变转速,则需要较大的比例增益。 温度控制系统:
在稳态下,积分项可以使温度保持在设定值,但如果环境温度发生变化,则需要较大的比例增益。 希望我的回答能够帮助您理解积分项在稳态下的作用。