目录
快速排序
历史:
基本思想:
主框架:
下面解释实现单次排序的几种版本:
1.Hoare版本
2. 挖坑法
3. 前后指针法
快速排序的实现包括递归与非递归:
1. 递归实现:(即开头的基本框架)
2. 非递归:(迭代)
下面我们通过栈来演示非递归实现快速排序:
快速排序
历史:
快速排序是Hoare(霍尔)于1962年提出的一种二叉树结构的交换排序方法
基本思想:
任取待排序元素序列中的一个元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后在左右子序列重复该过程,直到所有元素都排序在相应位置上为止
主框架:

上述为快速排序递归实现的主框架,我们可以发现它和二叉树的前序遍历十分相似
下面解释实现单次排序的几种版本:
1.Hoare版本
单趟动图演示:
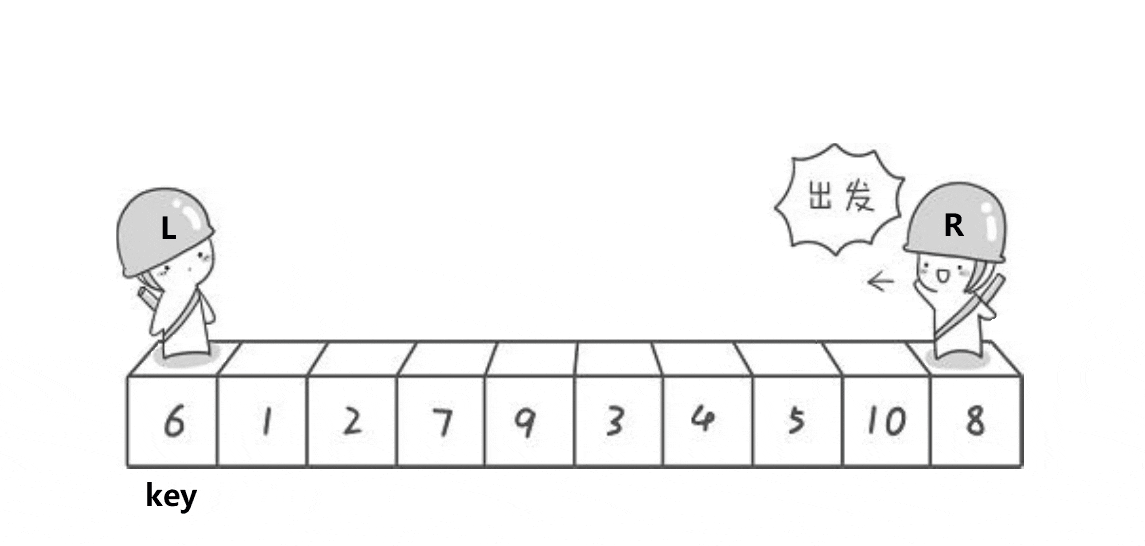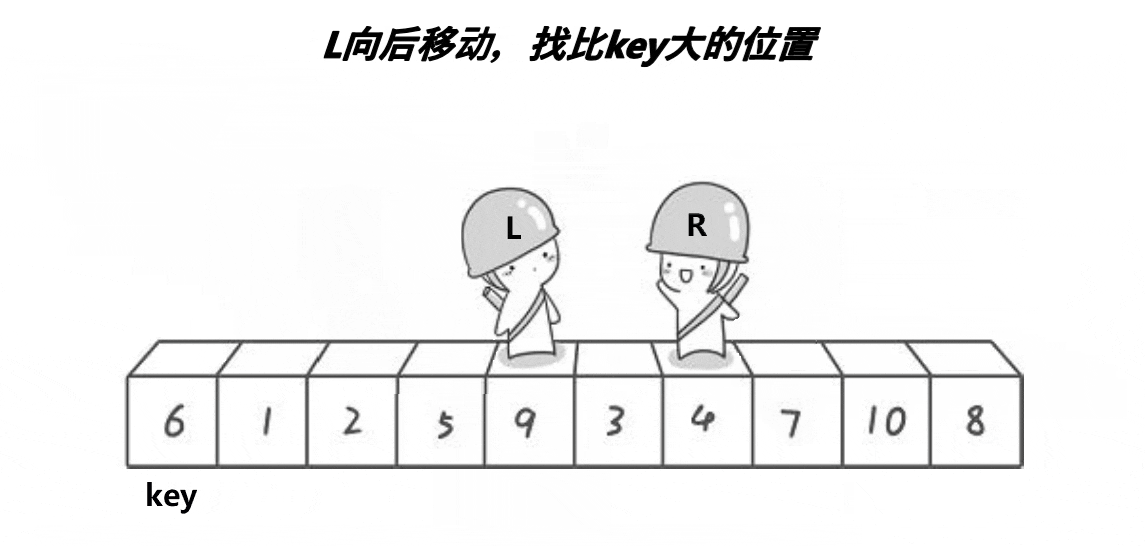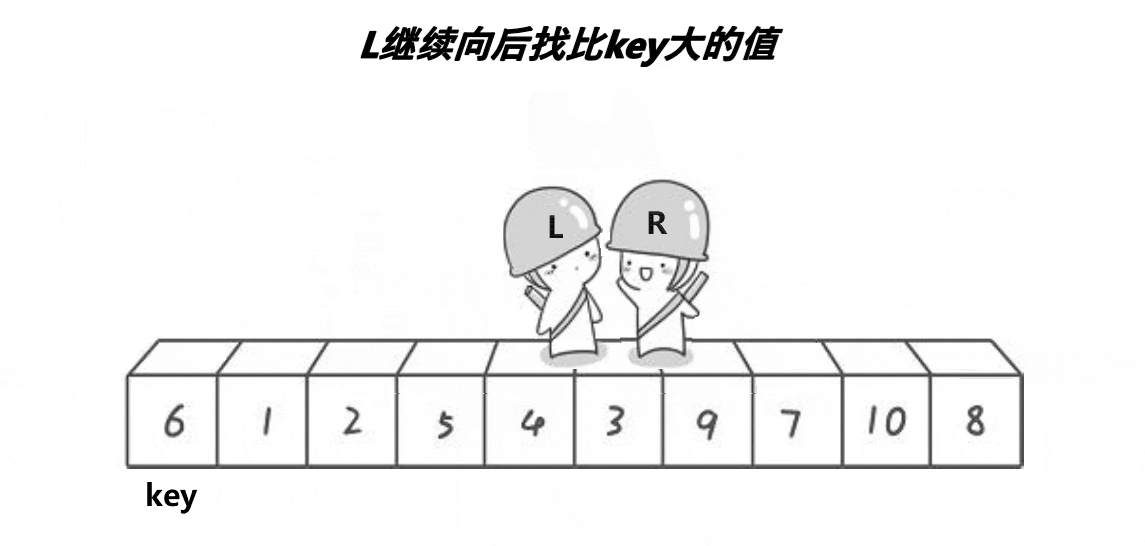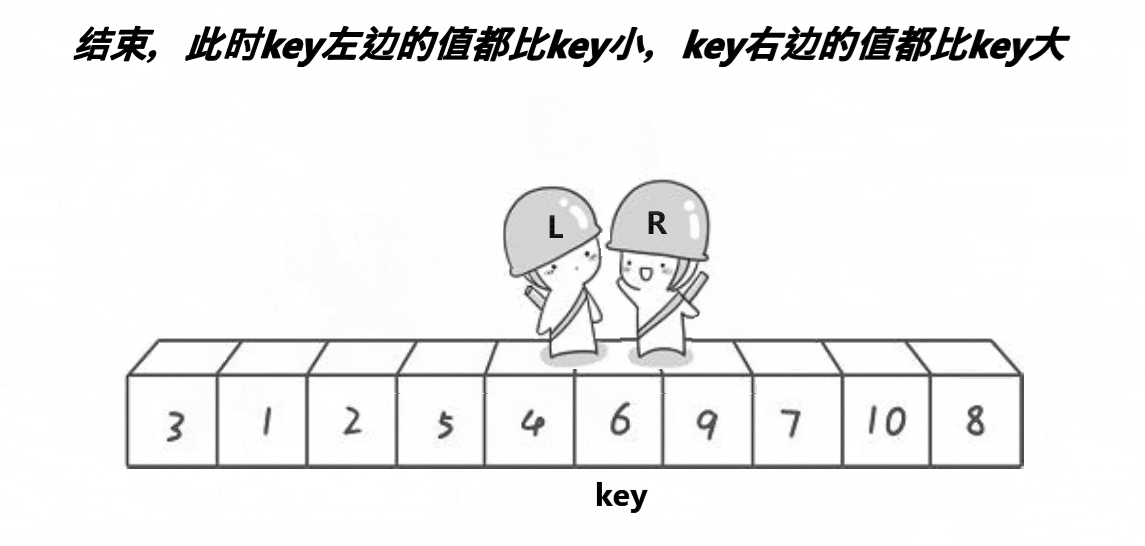
步骤:
选择基准值:通常选择序列的第一个元素或最后一个元素作为基准值。
设置两个int变量记录数组下标:一个记录序列的开始的下标(left),另一个记录序列的末尾的下标(right)。
开始分区:
- 先让right++,直到找到一个比基准值大的元素。
- 再让left--,直到找到一个比基准值小的元素。
- 交换这两个元素的位置,并继续right++。
- 重复上述步骤,直到left >= right。
- 注意:right先加,保证下一步骤与基准值交换的值小于基准值
交换基准值与right位置的值:此时,基准值左边的所有元素都比基准值小,基准值右边的所有元素都比基准值大。
代码实现:
int PartSort1(int* a, int left, int right) {
int key = left;
while (left < right) {
while(a[right] >= a[key]&&left < right) {
right--;
}
while(a[left] <= a[key]&&left < right) {
left++;
}
swap(&a[left], &a[right]);
}
swap(&a[key], &a[right]);
return left;
}2. 挖坑法
单趟动图演示:
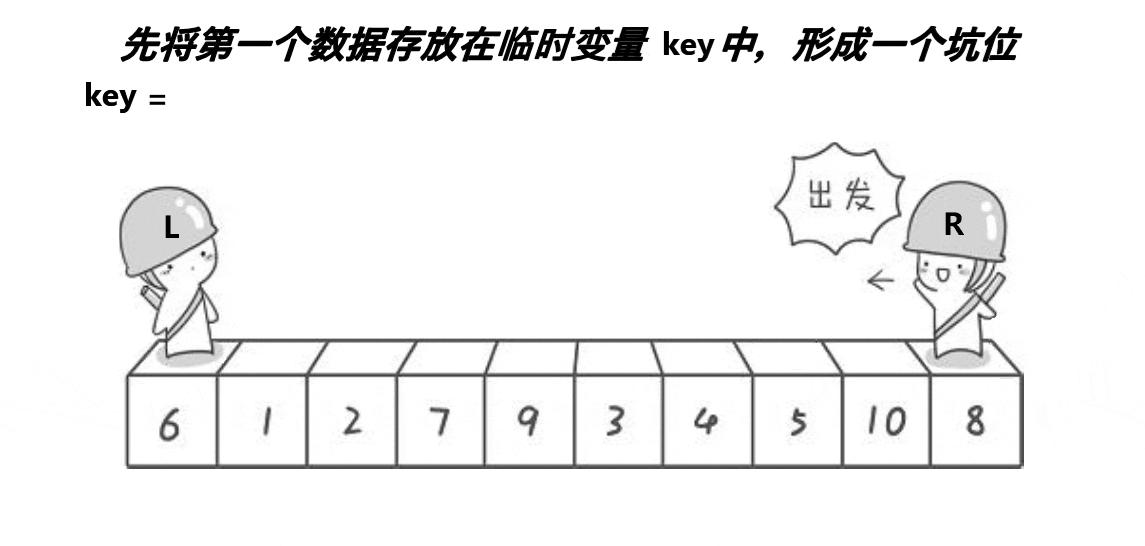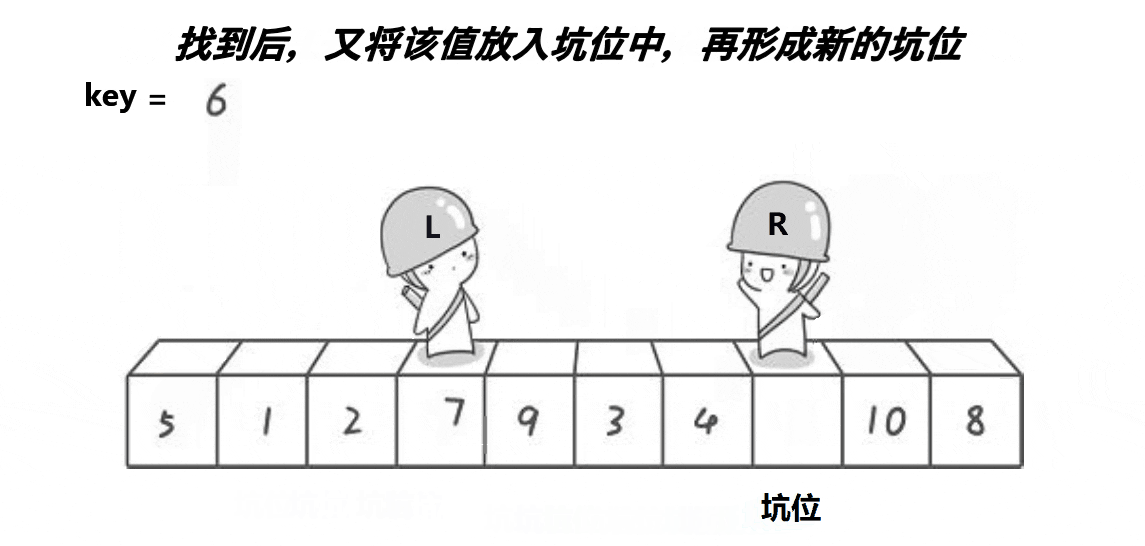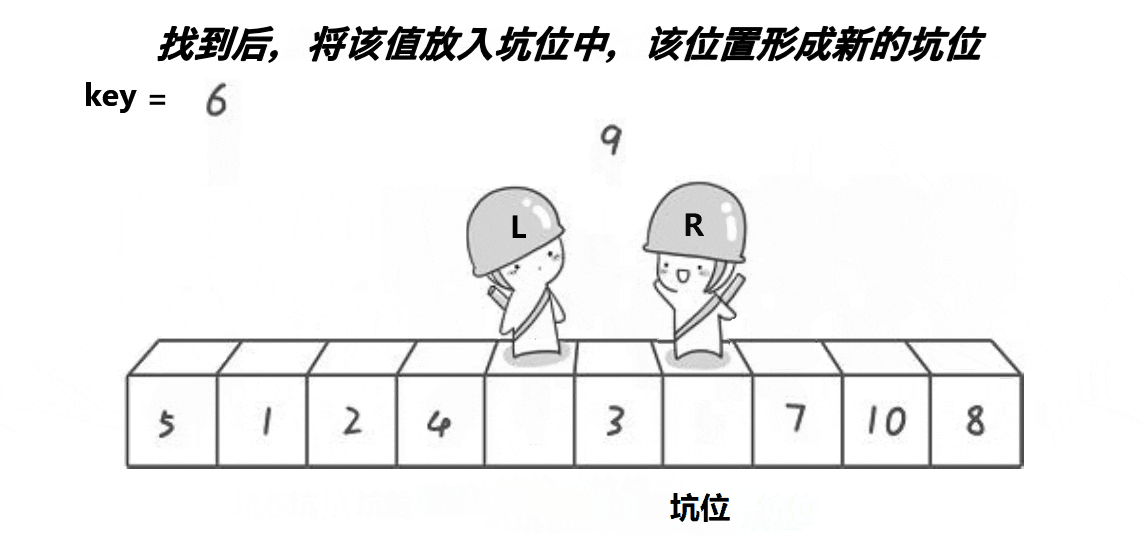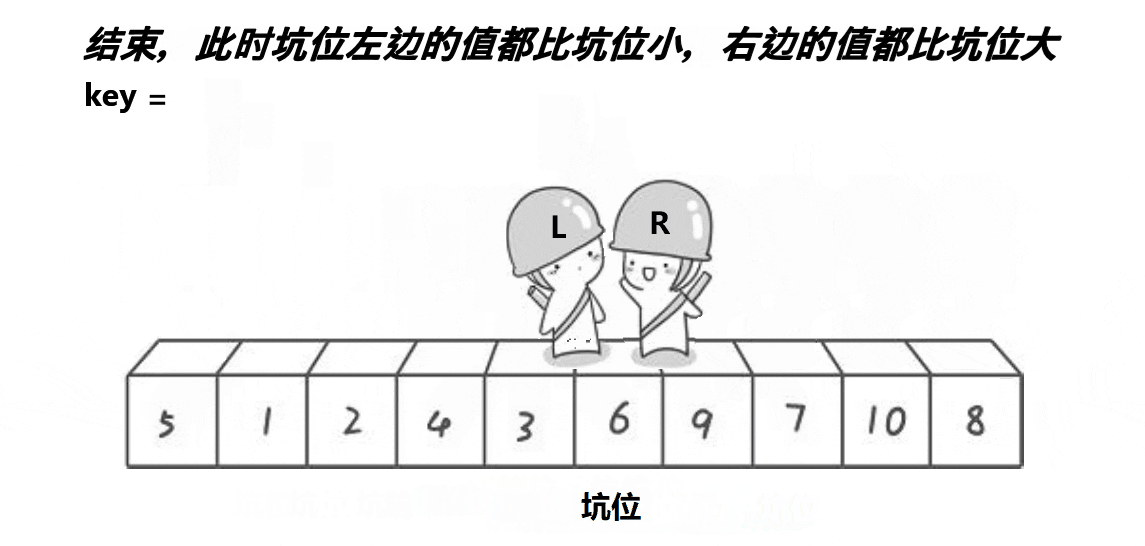
步骤:
选择基准元素:在待排序的序列中,选择一个元素作为基准元素(key)。这个元素可以是序列的第一个元素、最后一个元素或者任意一个元素,甚至是随机选取的一个元素。
挖坑:将基准元素从原位置移除,形成一个“坑”(hole)。
填坑:从序列的一端开始(可以是左端或右端),将遇到的第一个比基准元素小(或大)的元素填入坑中,并形成一个新的坑。这里有两种情况:
- 如果从右向左遍历,遇到比基准元素小的元素,则将其填入坑中,并继续从左向右遍历。这里代码实现选择该情况
- 如果从左向右遍历,遇到比基准元素大的元素,则将其填入坑中,并继续从右向左遍历。
- 此时,基准元素左边的所有元素都小于基准元素,右边的所有元素都大于或等于基准元素。
代码实现:
int PartSort2(int* a, int left, int right) {
int x = a[left];
int key = left;
while (left < right) {
while (a[right] >= x && left < right) {
right--;
}
a[key] = a[right];
key = right;
while (a[left] <= x && left < right) {
left++;
}
a[key] = a[left];
key = left;
}
a[key] = x;
return key;
}3. 前后指针法
单趟动图演示:
基本步骤:
- 从待排序的数组中选择一个元素(key)作为基准。通常选择第一个或最后一个元素作为基准,但也可以随机选择。
- 设置两个下标,一个记录序列的开始的下标(pre),即pre=left,另一个记录pre下一个元素的下标的下标(cur),即cur=pre+1;
- 当(cur<=right)时,循环执行:cur找比key小的元素,如果a[cur]<=a[key],交换a[cur]和a[pre],否则pre++,每次循环cur++
代码实现:
int PartSort3(int* a, int left, int right) {
int key = left;
int pre = left;
int cur = pre + 1;
while (cur <= right) {
if (a[cur] <= a[key] && ++pre != cur) {
swap(&a[cur], &a[pre]);
}
cur++;
}
swap(&a[key], &a[pre]);
return pre;
}快速排序的实现包括递归与非递归:
1. 递归实现:(即开头的基本框架)
void QuickSort(int* a, int left, int right) {
if (left >= right) {
return;
}
//int key = PartSort1(a, left, right);
//int key = PartSort2(a, left, right);
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}2. 非递归:(迭代)
在非递归版本中,我们使用栈(或队列)来保存待排序的子数组的起始和结束索引,而不是直接递归调用;栈相当于前序遍历,而队列相当于层序遍历
下面我们通过栈来演示非递归实现快速排序:
思路与步骤:
循环处理栈:当栈不为空时,执行以下步骤:
- 弹出栈顶的两个元素,它们分别表示当前子数组的起始和结束索引。
- 如果起始索引等于结束索引(即子数组只有一个元素),那么直接跳过,不需要排序。
- 调用
PartSort3函数对当前子数组进行划分,并返回划分后的基准索引key。- 弹出之前压入的起始和结束索引(因为已经处理过这个子数组了)。
- 根据
key的位置,决定下一步的操作:
- 如果
key等于起始索引left,说明基准左边的元素都已经排好序,只需要对基准右边的元素进行排序,所以将key + 1和right压入栈中。- 如果
key等于结束索引right,说明基准右边的元素都已经排好序,只需要对基准左边的元素进行排序,所以将left和key - 1压入栈中。- 如果
key既不等于left也不等于right,说明基准左右两边都有需要排序的元素,所以将left到key-1和key+1到right的子数组分别压入栈中- 2.完成:当栈为空时,表示所有子数组都已排序完成,此时整个数组也已排序完成。
代码实现:
typedef int StackNode;
typedef struct Stack {
StackNode* a;
int real;
int capacity;
}Stack;
void InitStack(Stack* p) {
assert(p);
p->a = NULL;
p->capacity = p->real = 0;
}
//扩容
void expansion(Stack*p) {
int newcapacity = p->capacity == 0 ? 4 : 2 * p->capacity;
StackNode* tmp = (StackNode*)realloc(p->a, sizeof(StackNode) * newcapacity);
if (tmp == NULL) {
perror("expansion::realloc::NULL");
exit(0);
}
p->a = tmp;
p->capacity = newcapacity;
}
//入栈
void Push(Stack*p,int x) {
assert(p);
if (p->capacity == p->real) {
expansion(p);
}
p->a[p->real++] = x;
}
//出栈
void Pop(Stack* p) {
assert(p);
p->real--;
}
void StackDestroy(Stack* p) {
assert(p);
free(p->a);
p->a = NULL;
p->capacity = p->real = 0;
}
//快排代码实现
void QuickSortNonR(int* a, int left, int right) {
if (left >= right) {
return;
}
Stack stack;
InitStack(&stack);
Push(&stack, left);
Push(&stack, right);
while (stack.real) {
left = stack.a[stack.real - 2];
right = stack.a[stack.real - 1];
if (left == right) {
Pop(&stack);
Pop(&stack);
continue;
}
int key = PartSort3(a, left, right);
Pop(&stack);
Pop(&stack);
if (key == left) {
Push(&stack, key + 1);
Push(&stack, right);
continue;
}
if (key == right) {
Push(&stack, left);
Push(&stack, key - 1);
continue;
}
Push(&stack, key + 1);
Push(&stack, right);
Push(&stack, left);
Push(&stack, key - 1);
}
StackDestroy(&stack);
}