C-数据结构-树状存储基本概念

news2024/10/6 16:26:51

‘’’
树状存储基本概念

深度（层数）
度（子树个数）
叶子
孩子
兄弟
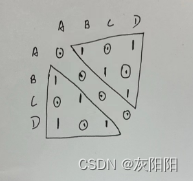
堂兄弟

二叉树：
满二叉树：
完全二叉树：

存储：顺序，链式

树的遍历：按层遍历，先序，中序，后序

‘’’
树是计算机科学中的一种重要数据结构。以下是关于树的基本概念和类型的详细介绍。

基本概念

深度（层数）：树中某个节点的深度是从根节点到该节点所经历的边的数目。根节点的深度为0。
度（子树个数）：一个节点的度是该节点的子节点（或子树）的个数。树的度是指树中所有节点的度的最大值。
叶子：叶子节点是指没有子节点的节点，即度为0的节点。
孩子：某个节点的直接下属节点称为该节点的孩子。
兄弟：具有同一个父节点的多个节点之间互称为兄弟。
堂兄弟：具有同一祖父节点但不同父节点的节点之间互称为堂兄弟。

二叉树

二叉树是一种特殊的树形结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树有以下几种特殊形式：

满二叉树：一个二叉树如果除了叶子节点外，每个节点都有两个子节点，并且所有叶子节点都在同一层次上，那么这个二叉树就是满二叉树。
完全二叉树：一个二叉树，如果除了最后一层外，每一层的节点都是满的，并且最后一层的节点都从左到右连续排列，这样的二叉树就是完全二叉树。

存储方式

顺序存储：利用数组存储二叉树。通常按层次顺序存储，从根节点开始，依次存入数组的相应位置。
链式存储：利用链表存储二叉树。每个节点使用一个结构体表示，结构体包含数据域和两个指针域，分别指向左子节点和右子节点。

树的遍历

按层遍历：从树的根节点开始，逐层遍历树中的所有节点。这种遍历方式也称为广度优先遍历。
先序遍历（前序遍历）：先访问根节点，然后递归地先序遍历左子树，最后递归地先序遍历右子树。
中序遍历：先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。
后序遍历：先递归地后序遍历左子树，然后递归地后序遍历右子树，最后访问根节点。
先中和中后能确定一颗树

以下是树的各种存储方式和遍历方式的示例代码：
在这里插入图片描述

顺序存储示例

#define MAXSIZE 100

typedef struct {
    int data[MAXSIZE];
    int size;
} SeqTree;

链式存储示例

typedef struct TreeNode {
    int data;
    struct TreeNode *left, *right;
} TreeNode;

树的遍历示例

// 先序遍历
void preOrder(TreeNode *root) {
    if (root != NULL) {
        printf("%d ", root->data);
        preOrder(root->left);
        preOrder(root->right);
    }
}

// 中序遍历
void inOrder(TreeNode *root) {
    if (root != NULL) {
        inOrder(root->left);
        printf("%d ", root->data);
        inOrder(root->right);
    }
}

// 后序遍历
void postOrder(TreeNode *root) {
    if (root != NULL) {
        postOrder(root->left);
        postOrder(root->right);
        printf("%d ", root->data);
    }
}

// 按层遍历
void levelOrder(TreeNode *root) {
    if (root == NULL) return;
    Queue q;
    initQueue(&q);
    enqueue(&q, root);
    while (!isEmpty(&q)) {
        TreeNode *node = dequeue(&q);
        printf("%d ", node->data);
        if (node->left != NULL) enqueue(&q, node->left);
        if (node->right != NULL) enqueue(&q, node->right);
    }
}