前言:本文讲解通过递归的方式实现二叉树的一些基本接口。
目录
通过左右子树的方式实现二叉树:
二叉树的遍历:
求二叉树结点的个数:
二叉树所有节点的个数:
二叉树叶子节点的个数:
求第k层节点的节点的个数 :
找二叉树中值为x的节点
求二叉树的高度:
构建二叉树:
销毁二叉树:
重头戏:中序遍历
判断二叉树是否是完全二叉树
通过左右子树的方式实现二叉树:
结构体的定义:
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;二叉树的遍历:
前序:根 ,左子树, 右子树
中序:左子树 ,根 ,右子树
后序: 左子树, 右子树, 根

根据上图分别走一遍前中后序:
前序:A ,B,NULL,NULL,C,NULL,NULL
中序:NULL,B,NULL,A,NULL,C,NULL
后序:NULL,NULL,B,NULL,NULL,C,A
想要理解前中后序需要了解递归
每一棵树都可以看成 根 左子树 右子树三部分组成。

代码实现:
//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("null ");
return;
}
printf("%c ", root->val);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
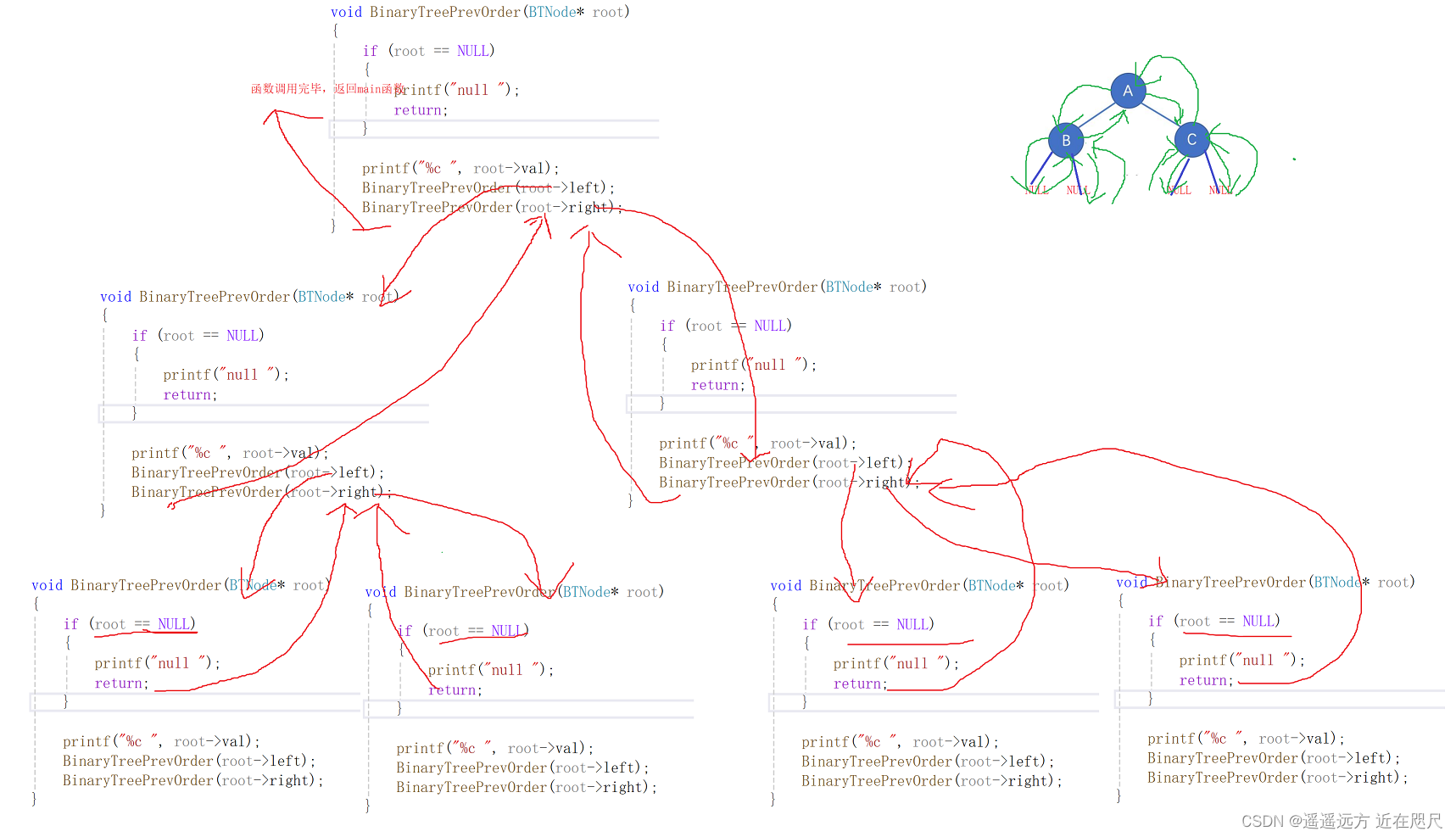
}深入理解代码:
以下是上面代码的函数递归调用的代码走读情况。
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("null ");
return;
}
BinaryTreeInOrder(root->left);
printf("%d ", root->val);
BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("null ");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d ", root->val);
}求二叉树结点的个数:
二叉树所有节点的个数:
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
将问题分解:
如果 root为NULL,返回0;
每个二叉树结点的个数等于左子树节点的个数+右子树节点的个数+根(1);
代码深入理解:

二叉树叶子节点的个数:
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left)+BinaryTreeLeafSize(root->right);
}将问题分解:
如果root为NULL,返回0;
如果左右子树为NULL,该节点为叶子节点就返回1;
二叉树的叶子节点的个数等于左子树叶子节点的个数+右子树叶子节点的个数。

求第k层节点的节点的个数 :
代码:
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root,int k)
{
if (root == NULL)
return 0;
if (k==1)//此时root不等于空
return 1;
return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}分解问题:
将问题可以看成: 第K层节点的个数 = 左子树第K-1层节点的个数+右子树K-1层节点的个数
如果root为NULL,返回0;
如果层数为1且该root不为NULL时,返回1

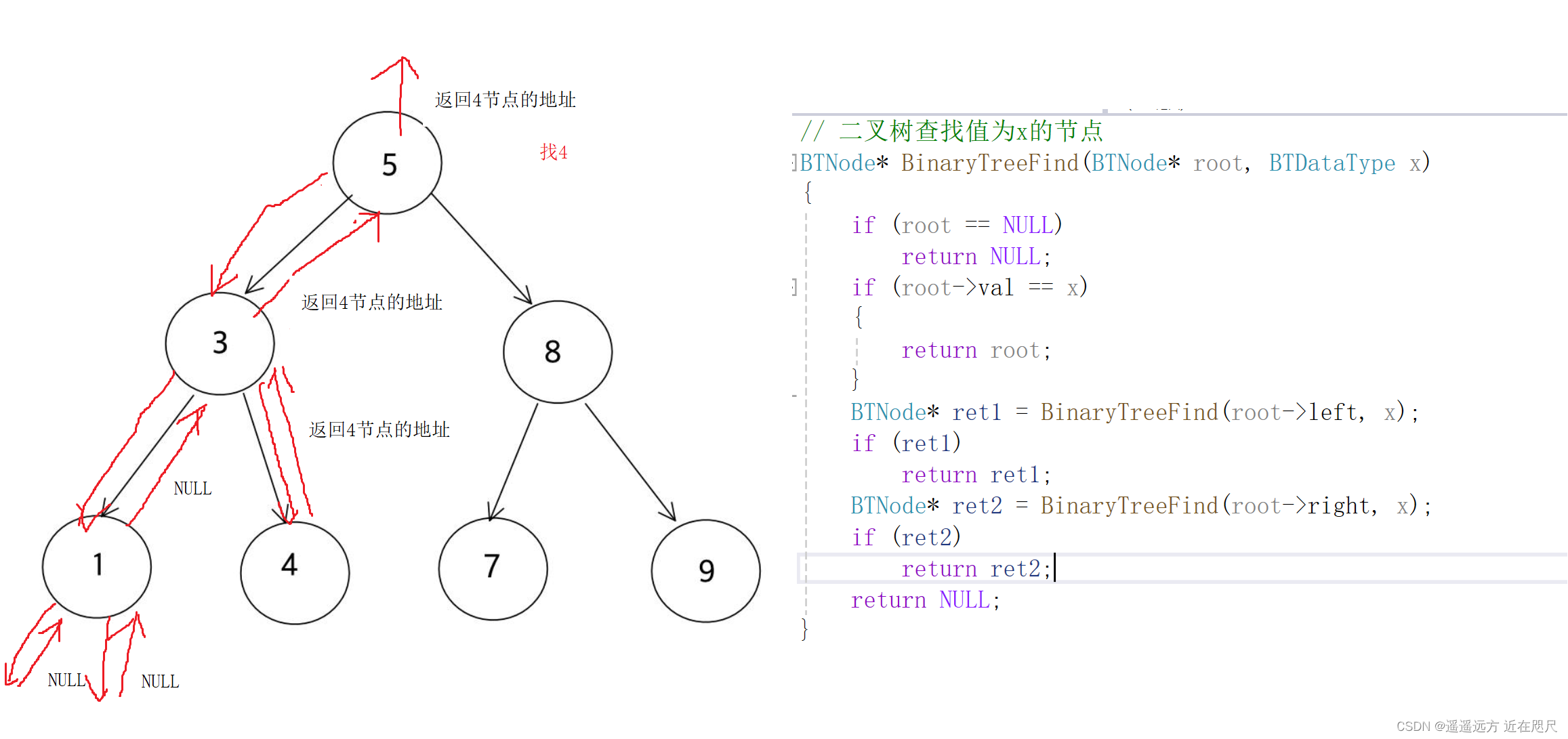
找二叉树中值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->val == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}注意:要创建一个变量接受返回值,然后再返回,如果直接用函数返回返回值,那么就会出现多次重复调用.
分解问题:
找整棵树的问题转化为,找左子树和找右子树的问题
如果root为NULL,返回NULL
如果找到root->val==x,直接返回该节点的地址,
如果左右子树都没有x这个值ULL.
求二叉树的高度:
代码:
//求二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int leftheight = BinaryTreeHeight(root->left);
int rightheight = BinaryTreeHeight(root->right);
return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}问题分解:
二叉树的高度 = 左右子树中高度最高的高度+1(根);

构建二叉树:
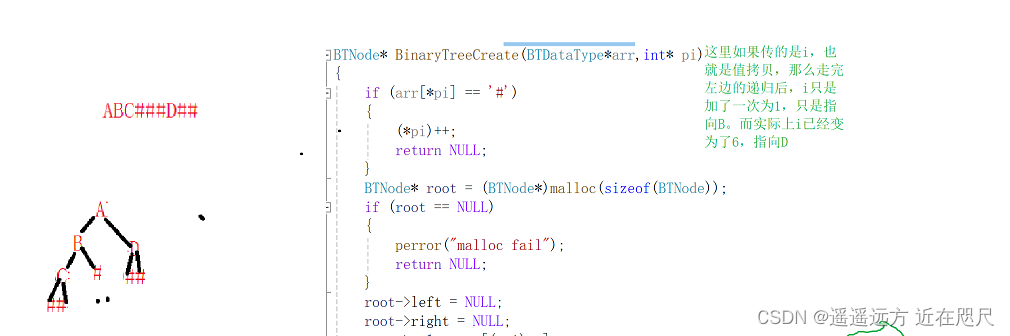
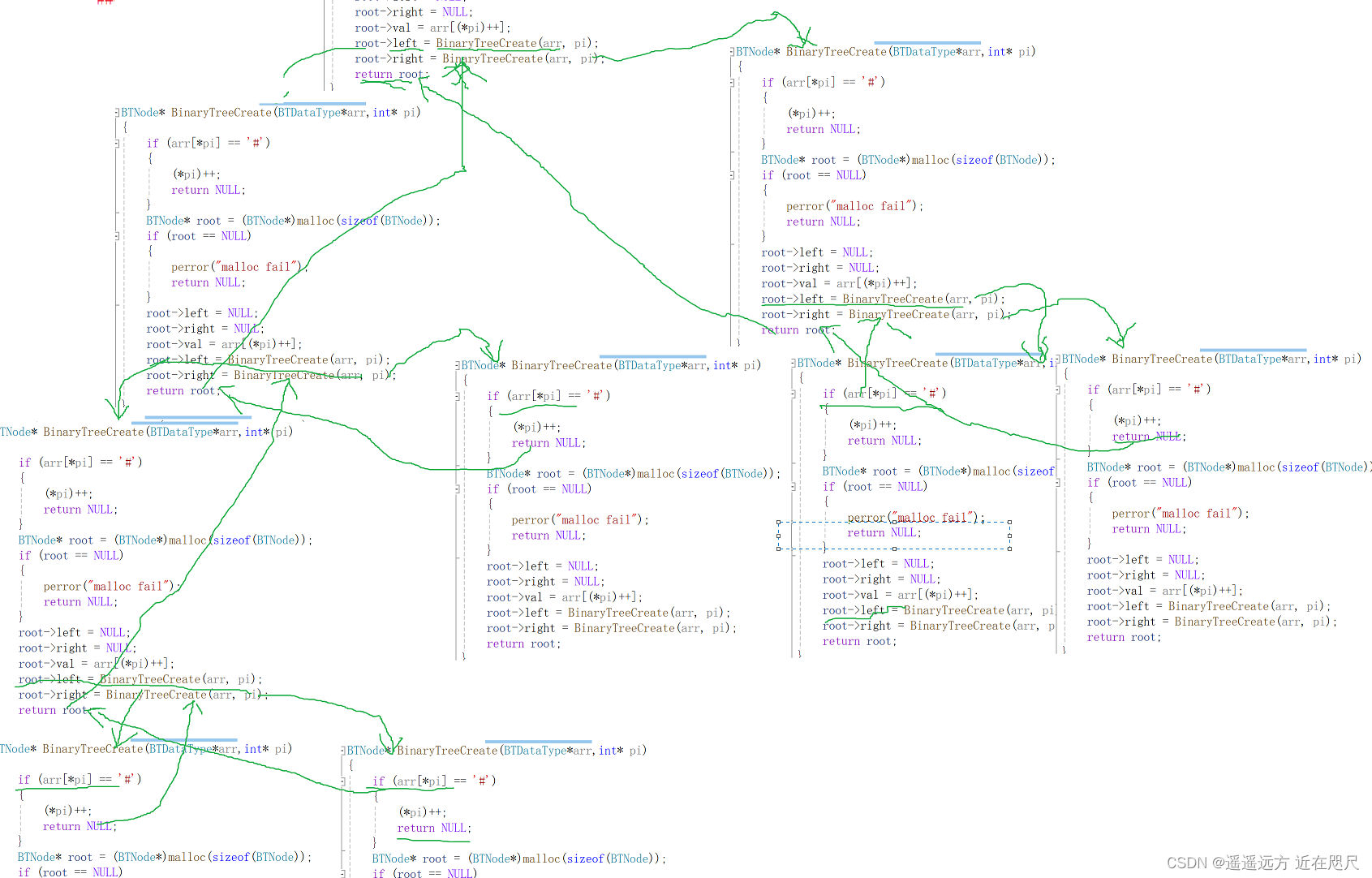
// 通过前序遍历的数组"ABC###D##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType*arr,int* pi)
{
if (arr[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
return NULL;
}
root->left = NULL;
root->right = NULL;
root->val = arr[(*pi)++];
root->left = BinaryTreeCreate(arr, pi);
root->right = BinaryTreeCreate(arr, pi);
return root;
}‘#’是NULL
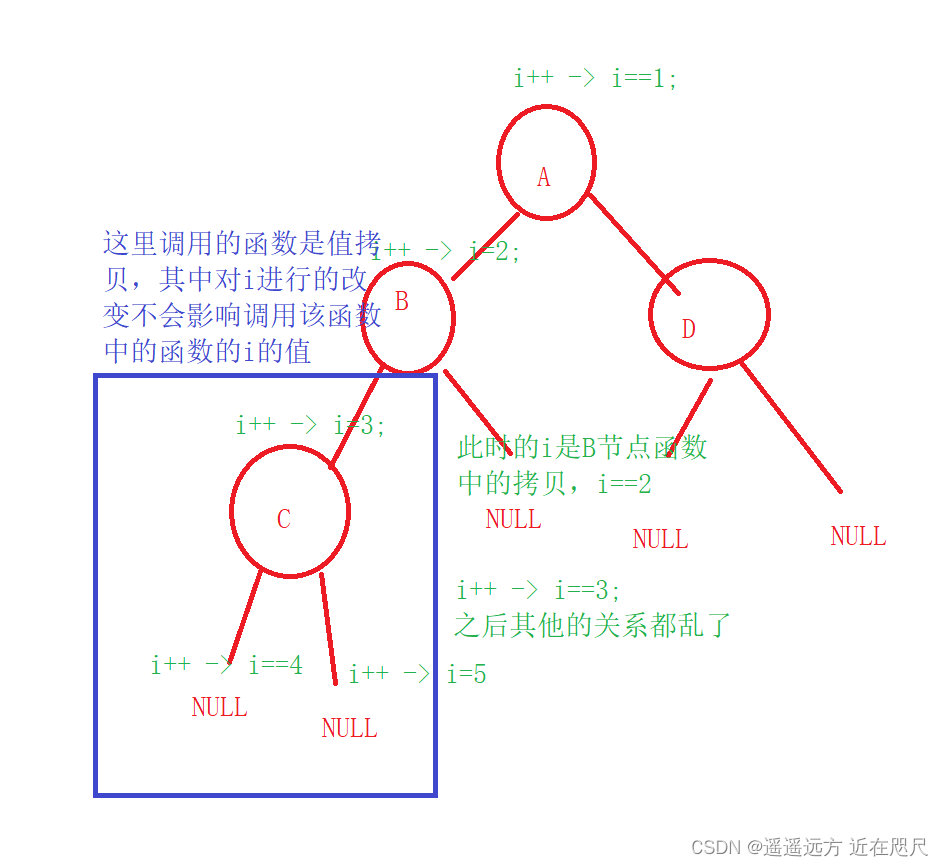
疑问:数组下标的指针pi,如果传值的话,就是临时拷贝,
如果传的是指针的话,因为是递归,调用递归的被调用的函数中i的改变不会改变调用该函数中的i的值,因为是值拷贝,如果还不理解的话,可以看一下关于函数值调用和址调用的区别。
销毁二叉树:
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
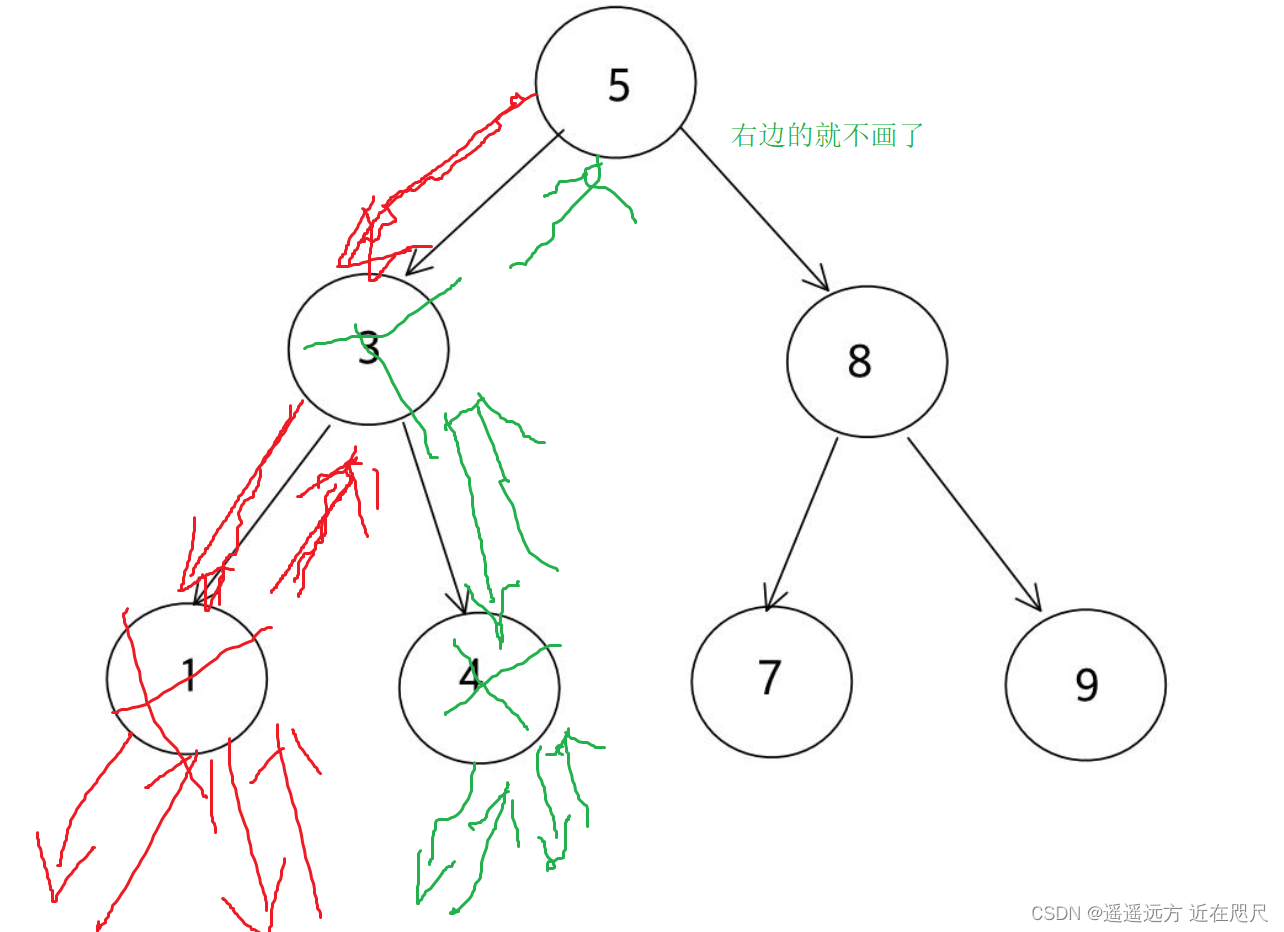
}二叉树的销毁采用后续遍历,如果采用前序或后序会非法访问,并且释放不干净。
重头戏:中序遍历
什么是中序遍历?
就是一层一层的遍历。
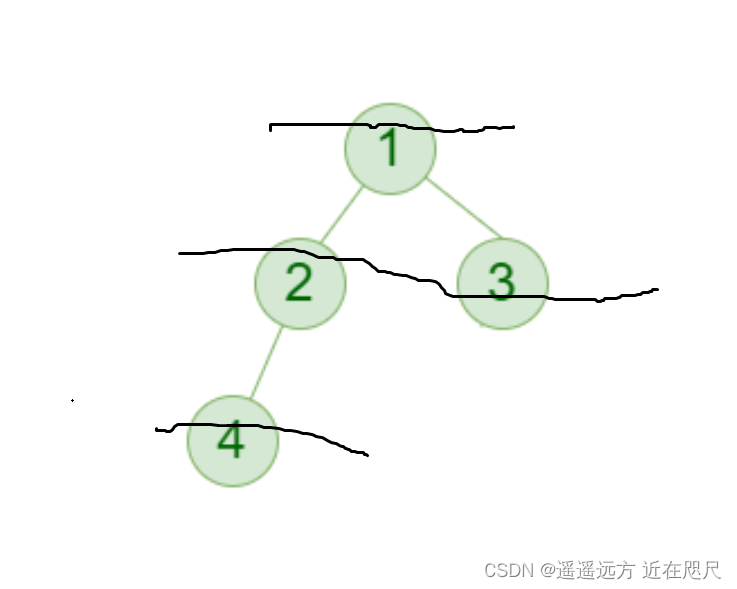
上图中序遍历的结果是: 1,2,3,4
那么如何实现中序遍历呢?
可以通过队列来实现,现将根节点入队列
每个元素出队列时,打印该节点的值,并将该元素的左右子树的根节点入队列,如果节点为NULL,那么就不入队列,直至队列为空为止。
这有一副流程图:
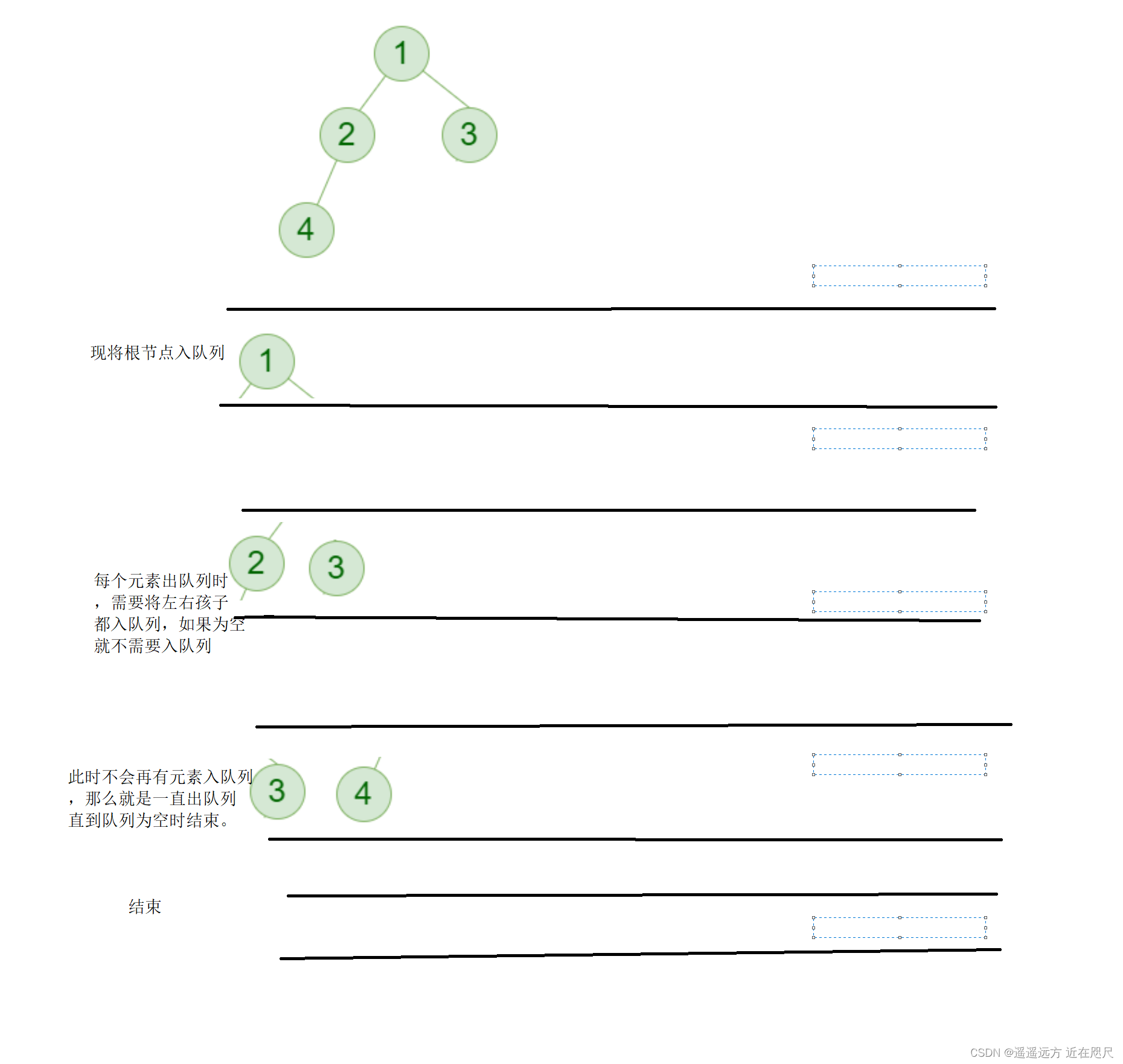
代码:
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);//初始化队列
if(root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);//获得队头数据
QueuePop(&q);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
printf("%c ", front->val);
}
}注意:这里队列中的存储的元素的数据类型为,二叉树节点的指针。
完成这个代码需要用到以前写过的队列的代码:
如果有需要这里有链接,数据结构: 实现初阶数据结构的代码 (gitee.com),如果不会队列的话,也可以看我以前的博客写的队列。
typedef BTNode* QDataType;
typedef struct QNode
{
struct QNode* next;
QDataType val;
}QNode;判断二叉树是否是完全二叉树
这个思路跟上面中序遍历的思路一样,都需要用到队列,不同的是,中序遍历不将NULL入队列,
而这个如果左右子树的根为NULL,仍入队列。
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
return false;
}
return true;
}思路: 第一次出队列的元素为NULL时,就一直将队列中的元素一直出队列,如果全为NULL则为完全二叉树,只要有一个不为NULL,那么就不是完全二叉树。
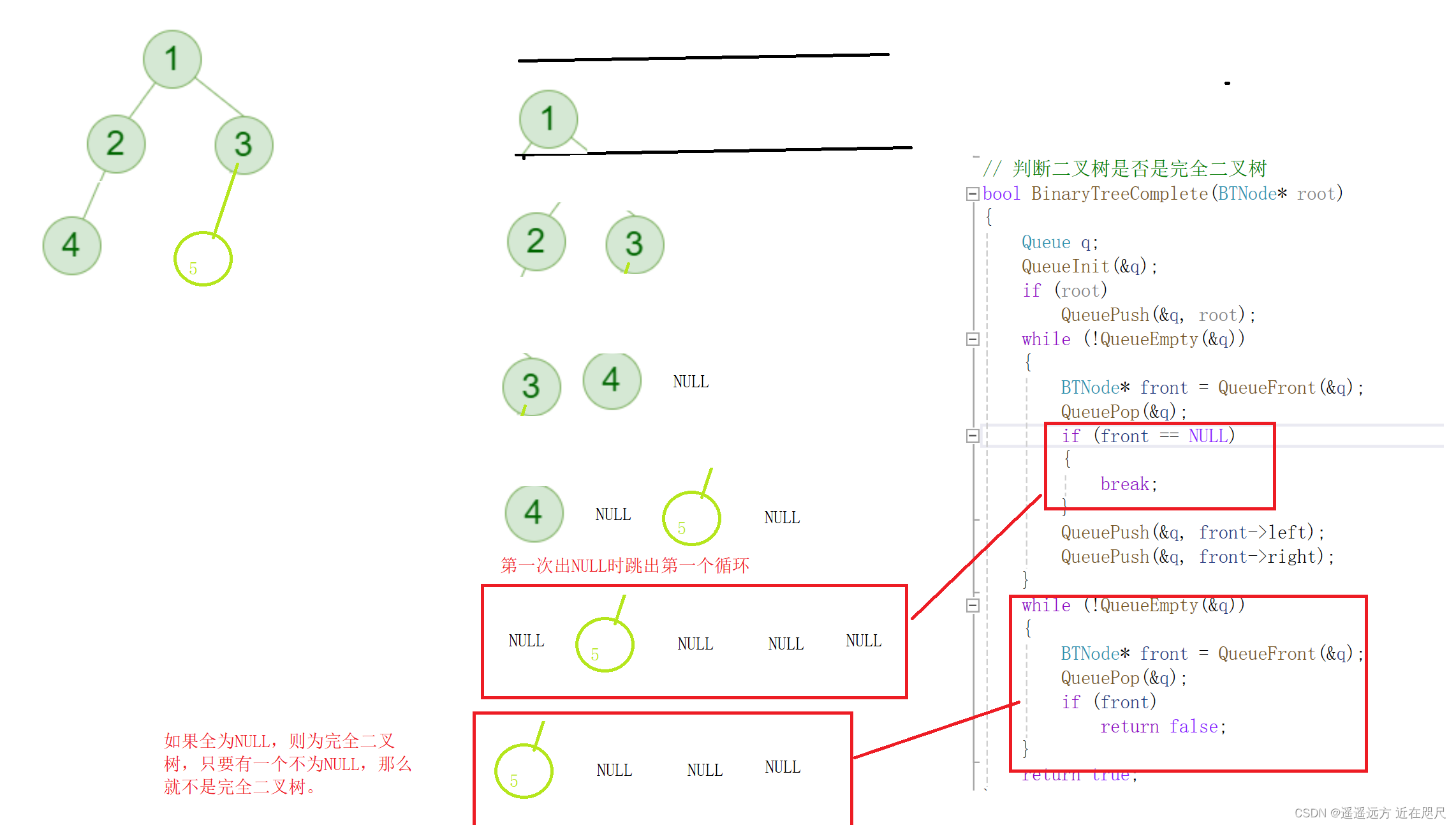
结语:这就是今天的分享,希望看到这篇博客的人都能有所收获。