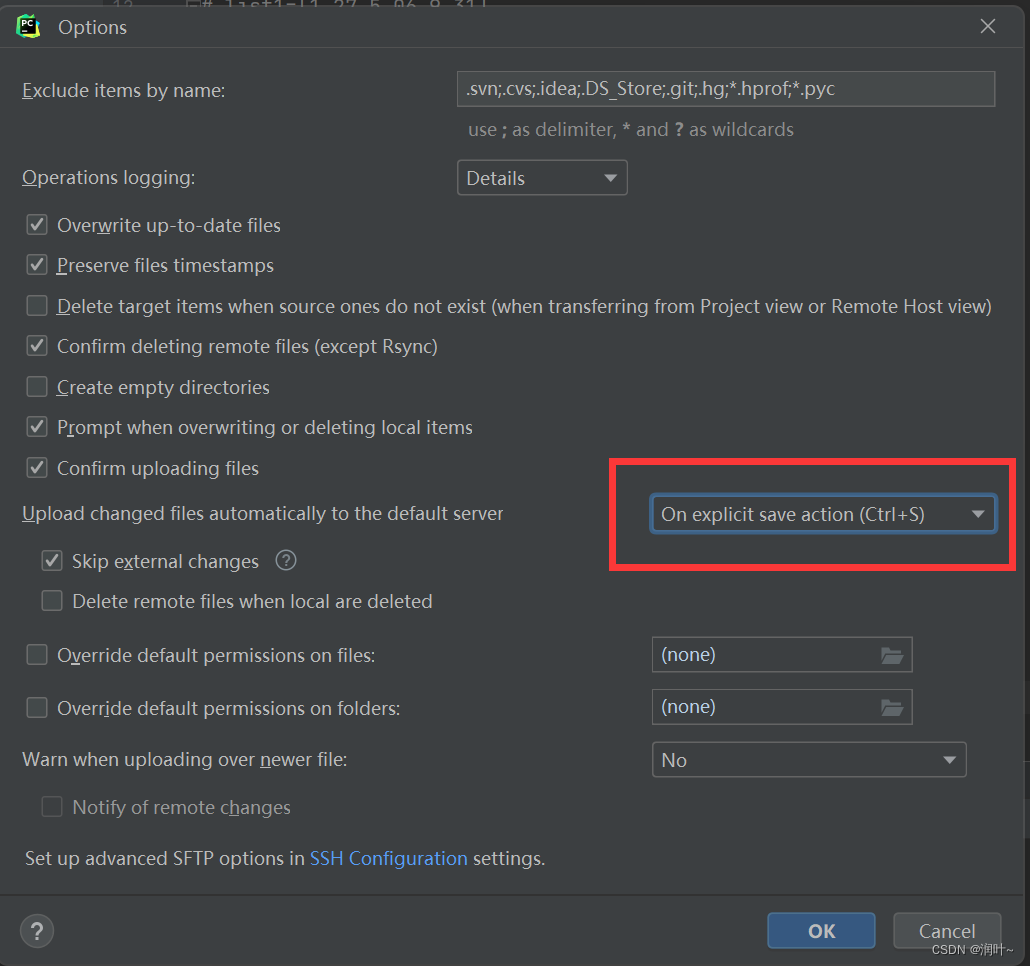
一、算法逻辑
想要轻松形象理解Kruskal算法的算法逻辑，视频肯定比图文好。
小编看过很多求相关的教学视频，这里选出一个我认为最好理解的这一款安利给大家。
因为他不仅讲解细致，而且还配合了动画演示，可以说把一个抽象的东西讲的非常的形象了。
B站链接：【最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示】
二、JAVA实现
1、实现这个算法，要建立一个图，才可以，这里小编直接给一个，
基于邻接矩阵的图：
public class GraphByMatrix {
private char[] arrayV;//顶点数组
private int[][] matrix;//矩阵，存放每一个边的权重
private boolean isDirect;//是否是有向图
/**
* 构造方法
*
* @param size 代表当前顶点的个数
* @param isDirect 是否是有向图，true是有向图
*/
public GraphByMatrix(int size, boolean isDirect) {
this.arrayV = new char[size];//顶点的个数是size
matrix = new int[size][size];
for (int i = 0; i < size; i++) {
Arrays.fill(matrix[i], Constant.MAX);
}
this.isDirect = isDirect;
}
/**
* @param srcV 起点
* @param destV 终点
* @param weight 权值
*/
public void addEdge(char srcV, char destV, int weight) {//重载之一，用来建立普通图
int srcIndex = getIndexOfV(srcV);
int destIndex = getIndexOfV(destV);
matrix[srcIndex][destIndex] = weight;
//如果是无向图 那么相反的位置 也同样需要置为空
if (!isDirect) {
matrix[destIndex][srcIndex] = weight;
}
}
/**
* @param srcIndex 起点
* @param desIndex 终点
* @param weight 权重
*/
public void addEdge(int srcIndex, int desIndex, int weight) {//重载两个之一，用来建立最小生成树
matrix[srcIndex][desIndex] = weight;
//如果是无向图 那么相反的位置 也同样需要置为空
if (!isDirect) {
matrix[desIndex][srcIndex] = weight;
}
}
/**
* 获取顶点V的下标
*
* @param v
* @return
*/
private int getIndexOfV(char v) {
for (int i = 0; i < arrayV.length; i++) {
if (arrayV[i] == v) {
return i;
}
}
return -1;
}
public void printGraph() {
for (int i = 0; i < arrayV.length; i++) {
System.out.print(arrayV[i] + " ");
}
System.out.println();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] == Constant.MAX) {
System.out.print("∞ ");
} else {
System.out.print(matrix[i][j] + " ");
}
}
System.out.println();
}
}
/**
* 定义了一个边的抽象类
* 用来存储边的
*/
static class Edge {
public int srcIndex;
public int destIndex;
public int weight;//权重
public Edge(int srcIndex, int destIndex, int weight) {
this.srcIndex = srcIndex;
this.destIndex = destIndex;
this.weight = weight;
}
}
public static void main(String[] args) {
}
}接下来对克鲁苏卡尔算法进行实现：
因为树一定是无向图，而无向图，用邻接矩阵表示，有一个特点，等一下会用到，以下边这个无向图为例：
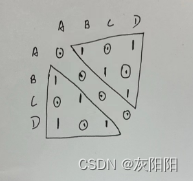圆圈代表不存在边，1代表有边
我们发现这个矩阵代码
/**
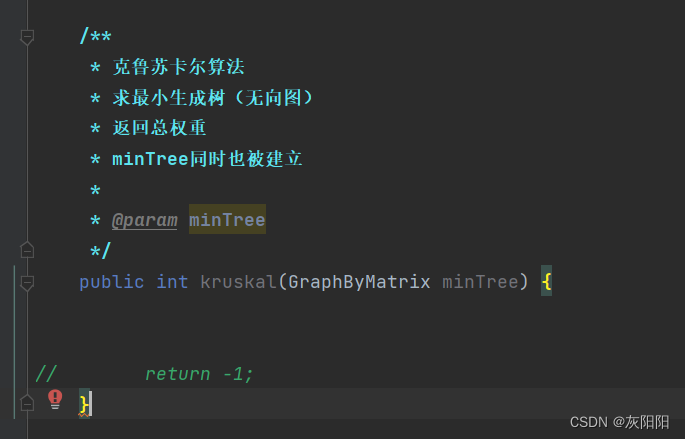
* 克鲁苏卡尔算法
* 求最小生成树（无向图）
* 返回总权重
* minTree同时也被建立
*
* @param minTree
*/
public int kruskal(GraphByMatrix minTree) {
/**
* 第一步：对所有的边进行排序（从小到大）
*/
PriorityQueue<Edge> minHeap = new PriorityQueue<>();//建立一个小根堆来实现排序
int n=arrayV.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
/*
* i<j的原因：
* //因为是无向图，所以根据对称性，只用录入一个方向的边的权值即可
* */
if (j < i && matrix[i][j] != Constant.MAX) {//邻接矩阵的元素如果是Constant.Max说明边不存在
minHeap.offer(new Edge(i, j, matrix[i][j]));//i到j，权值是matrix[i][j]
}
}
}
//程序到达此处，已经排序好所有的边了
//初始化查集后，每一个元素都是独立的集合
UnionFindSet unionFindSet=new UnionFindSet(n);//定义一个并查集，大小就是图顶点数
int size=0;//记录已经寻找到的边的个数，只要等于n-1，最小生成树就找到了
int totalWeight=0;//用来记录最小总权值
while(size<n-1&&!minHeap.isEmpty()){//如果不加!minHeap.isEmpty()这个条件，此图若没有最小生成树（所给的图不是连通图），那么程序会死循环
Edge edge=minHeap.poll();//出一个边
int src=edge.srcIndex;//起点下标
int des=edge.destIndex;//终点下标
if(!unionFindSet.isSameUnionFindSet(src,des)){//不是同一个集合，进来（如果是同一个集合，就代表形成了环！）
minTree.addEdge(edge.srcIndex,edge.srcIndex,edge.weight);//给最小生成树增加一条边
size++;//尺寸加加
unionFindSet.union(src,des);//合并两个顶点构成的边
totalWeight+=edge.weight;
}
}
if(size==n-1){
return totalWeight;
}else{//size!=n-1说明所给的图，不是连通图，找不到最小生成树
return -1;//返回一个无效值
}
}是关于对角线对称的，这个要记住等一下会用到。
代码加注释：
