文章目录
- 最小生成树
- 普里姆算法
- 实现过程
- 代码实现
最小生成树
什么是最小生成树?
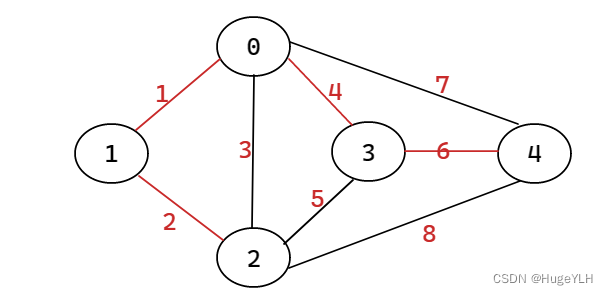
对于如图所示的带权无向连通图来说:从图中任意顶点出发,进行dfs或者bfs便可以访问到图中的所有顶点,因此连通图中一次遍历所经过的边的集合以及图中所有顶点的集合就构成了该图的一颗生成树。
其中把具有权之和最小的生成树叫做最小生成树。
如图中: 红色线表示的就是这棵树的最小生成树。
最小生成树可以应用到许多实际生活中,比如说求 用尽可能小的造价修建若干条高速公路,求 n个城市连接在一起的最短路径等等。。
普里姆算法
普里姆算法是一种构造性算法,用于求得一个带权无向连通图的最小生成树。
普里姆算法规定:
- G = (V,E) 是一个带权无向联通图。 V表示图中的所有顶点集合,E表示点与边之间的关系
- T=(U,TE)是一颗最小生成树。U表示最小生成树的点的集合,TE表示最小生成树中的边集合。
假设我们要从 s点出发构建一颗最小生成树:
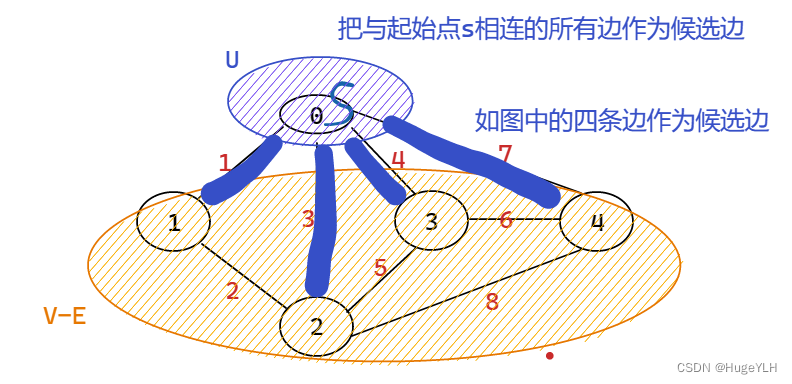
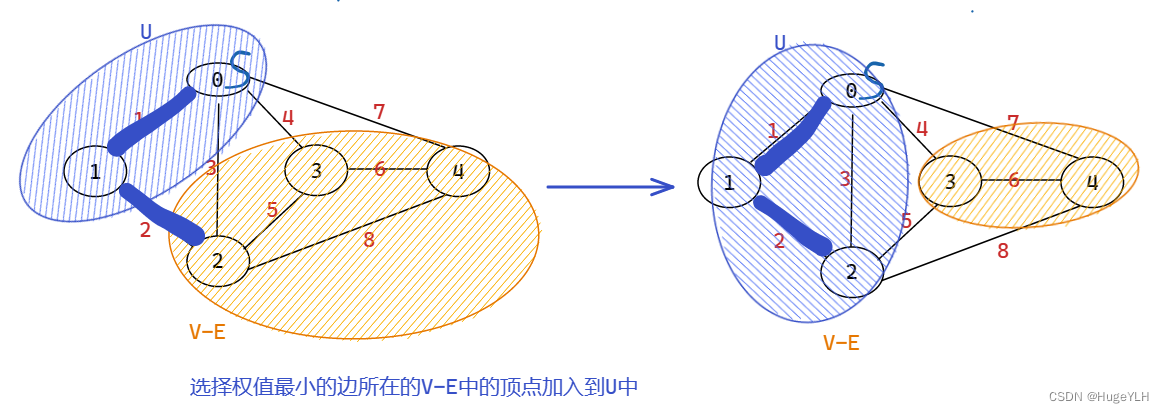
- 把s点加入U中,与s相邻的所有边作为侯选边,选出所有侯选边中权值最小的边,并且把这条边所在的V中的顶点加入到U中,并且把这个权值最小的边加入到TE中。
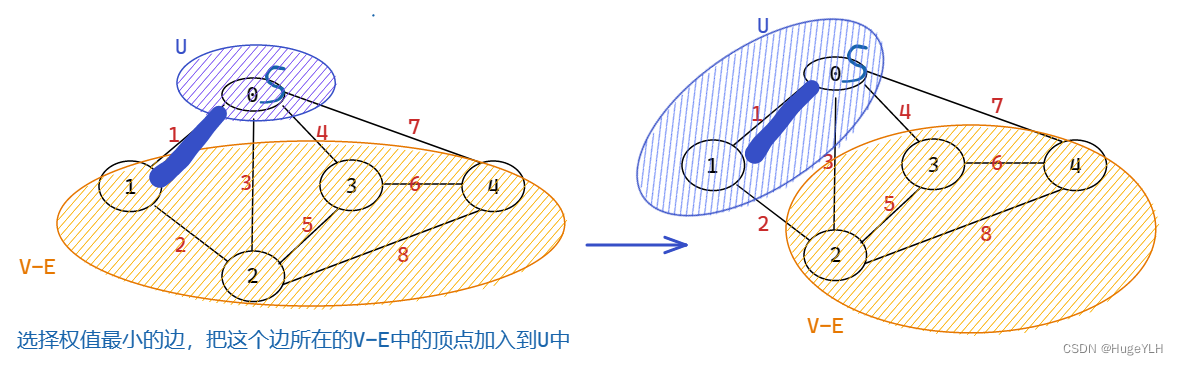
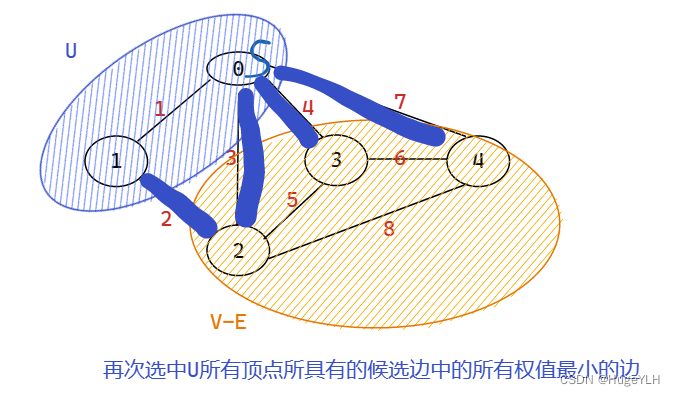
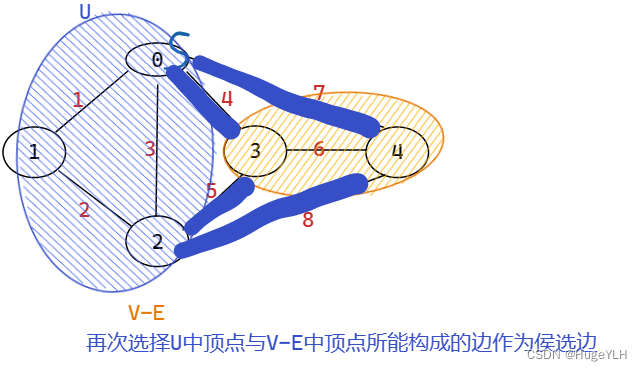
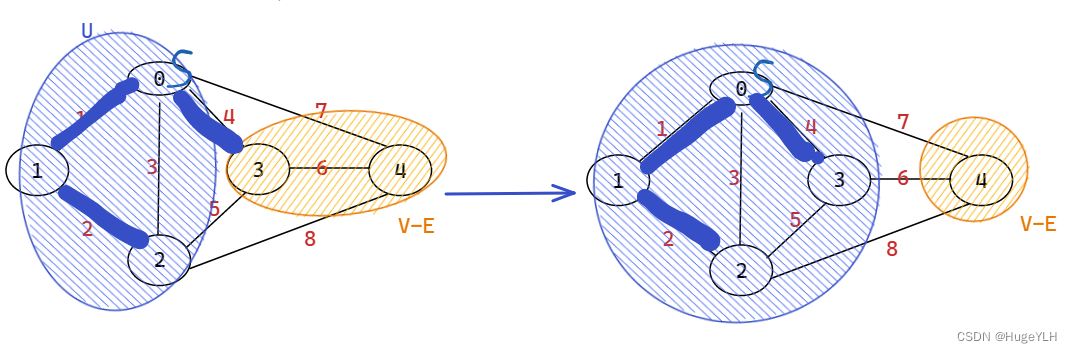
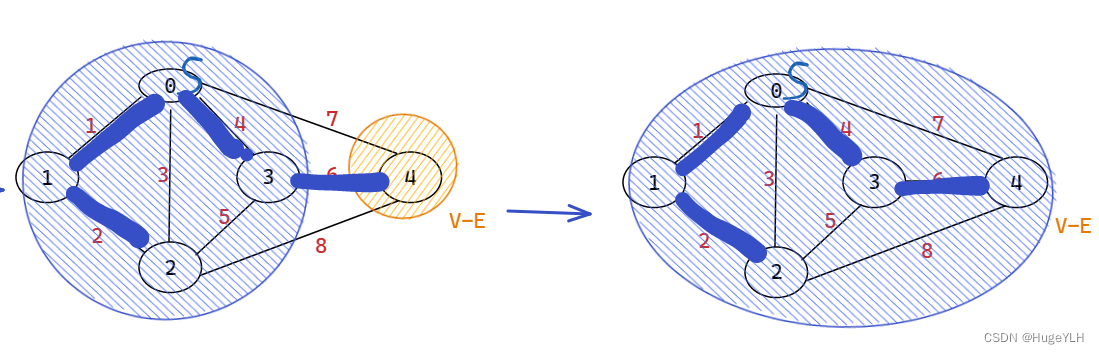
- 更新最小生成树的U与带权无向连通图的V-E,同时修改候选边:考察在V-E中所有顶点,把具有最小权值的边取代之前的候选边,然后重复步骤1.
图解步骤:
实现过程
我们使用两个辅助数组:
closest 与 lowcost
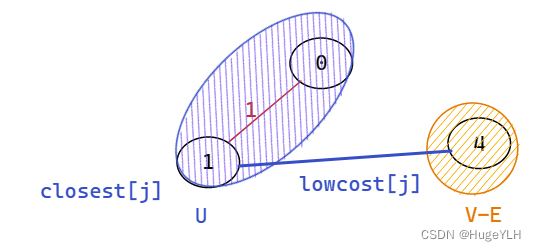
closest表示在U(最小生成树的顶点集合)中存储的顶点编号
lowcost表示存储该边的权值最小值
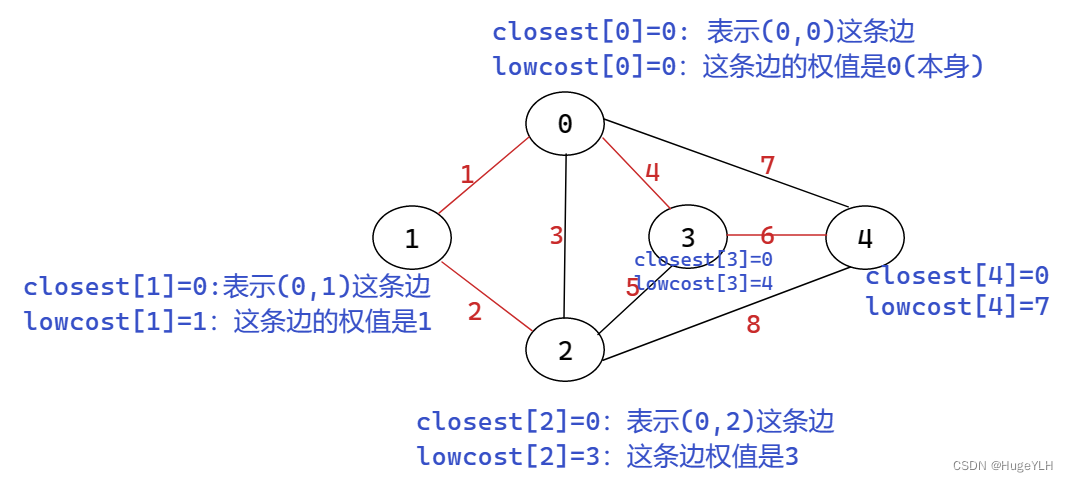
由此:
- closest[i] = p: 表示 p -> i 这两个点
- lowcost[i]:s->i这两个点所表示的边的权值。
实现过程:
-
U(s) V-E(1,2,3,4) 从V-E顶点中选择一个lowcost[i]最小的点,这个点 i 就是第一次找到的点,图中即 i=1,即构造了最小生成树(0,1),将顶点i 加入到U中,然后置lowcost[i] 为零,表示已经找到这个点了。
-
然后修正这两个数组: 修正后如下:
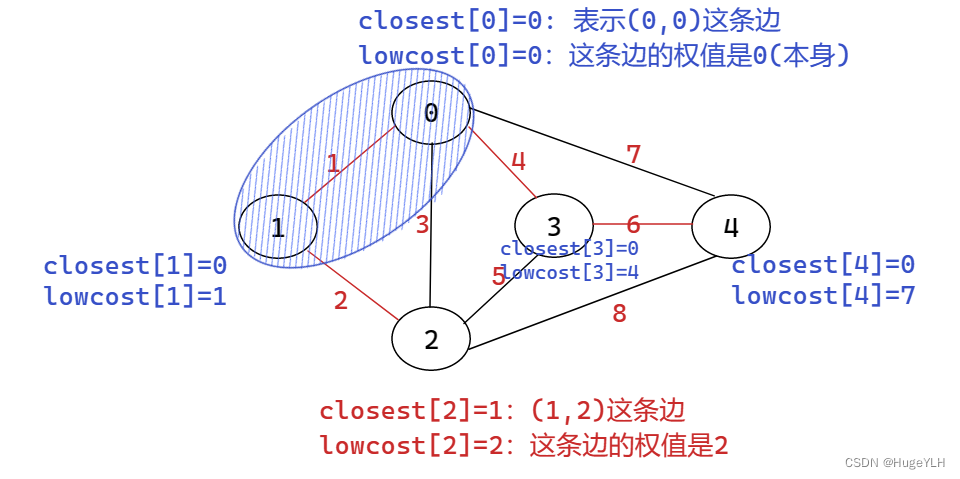
-
然后重复在V-E(2,3,4)中找到lowcost[i]最小的点,为lowcost[2] =3 ,此时i=2,然后以这个点构造第二条边:U(0,1,2),将顶点 i加入到U中,置lowcost[i]=0,然后修正数组,重新执行上面的操作
代码实现
首先要构建邻接矩阵:关于邻接矩阵与邻接表:
邻接矩阵与邻接表
普里姆算法:Prim
#include <iostream>
#include <string>
using namespace std;
constexpr const auto INF = 0x3f3f3f3f;
#define MAXN 100
//点集合
struct Vetrix
{
int id;
string info;
};
struct Graph
{
int n, e; //n:点数 e:边数
int edge[MAXN][MAXN]; //边集合
Vetrix v[MAXN]; //点集合
};
//创建邻接矩阵
void createGraph(Graph& g, int A[][5], int n, int e)
{
g.e = e;
g.n = n;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
g.edge[i][j] = A[i][j];
}
}
}
//普里姆算法
void Prim(Graph& g, int u)
{
//以u为最小生成树的起点
//两个辅助数组
int closest[MAXN], lowcost[MAXN];
for (int i = 0; i < g.n; i++)
{
closest[i] = u; //i: 顶点
lowcost[i] = g.edge[u][i]; edge[u][i]: u->i 这条边所具有的权值
}
int min, k;
for (int i = 1; i < g.n; i++)
{
min = INF, k = -1;
for (int j = 0; j < g.n; j++)
{
//lowcost[j] != 0 表示所选的点不能是U中的点,只能是V-E中的
//lowcost[j] < min 表示依次选取权值最小的边
if (lowcost[j] != 0 && lowcost[j] < min) //在V-E中找出离U最近的顶点
{
min = lowcost[j];
k = j; //k为最近顶点编号
}
}
//k:记录了权值最小的边在V-E中的顶点编号
//min:记录了这个最小权值
printf(" 边(%d -> %d) 权值:%d\n", closest[k],k, min);
//修正数组
lowcost[k] = 0; //这个边已经选过了
for (int j = 0; j < g.n; j++)
{
//以k作为起点,寻找与k点连接的边的权值是否比之前记录的权值小
if (lowcost[j] != 0 && g.edge[k][j] < lowcost[j])
{
lowcost[j] = g.edge[k][j]; //更新为最小权值
closest[j] = k; //记录这个点
}
}
}
}
int main()
{
Graph g;
int n = 5, e = 8;
int A[][5] = {
{0,1,3,4,7},
{1,0,2,INF,INF},
{3,2,0,5,8},
{4,INF,5,0,6},
{7,INF,8,6,0}
};
createGraph(g, A, n, e);
Prim(g, 0);
return 0;
}
运行如下: